交直流混合系统潮流计算的方法基本上是纯交流系统潮流计算方法的推广,主要有统一迭代法和交替迭代法。由于附加的直流功率项与交流节点参数无关,纯交流系统潮流计算对应部分方程的雅可比矩阵的子矩阵H、N、J和L没有发生变化。有关交直流混合系统功率法方程和矩阵形式,在后续的多端直流潮流计算中还将详细介绍。......
2023-06-29
从图3.11中可以看到在直流系统两侧的交流母线电压发生变化时,无论直流系统的运行方式是否会发生转换,在直流系统的每一个状态运行我们总能够确定直流系统的四个直流参数,根据第2章中建立的潮流计算模型,直流系统的参数为Xdc=[Id、Udr、Udi、Tr、Ti、α、γ]T。如果知道直流系统的四个直流参数,那么交直流系统的潮流可解。按照上节中的分析,直流系统两端交流母线电压变化时可分为8个运行状态:
(1)初始状态A:已知:Id=Ids、α=αs、γ=γs、Udr=Uds;未知:Tr、Ti和Udi。
(2)整流侧交流母线电压变化时:
状态B:已知:Id=Ids、Tr=Trmax、γ=γs、Udr=Uds;未知:α、Ti和Udi。
状态C:已知:Id=Ids-Im、Tr=Trmax、α=αmin、Ti=Tio;未知:Udr、γ和Udi。
状态D:已知:Id=Ids、Tr=Trmin、γ=γs、Udr=Uds;未知:α、Ti和Udi。
逆变侧交流母线电压变化时:
状态E:已知:α=αs、Id=Ids、Ti=Timin、γ=γs;未知:Tr、Udr和Udi。
状态F:已知:Id=Ids、Tr=Trmax、Ti=Timin、γ=γs;未知:α、Udr和Udi。
状态G:已知:Id=Ids-Im、Tr=Trmax、Ti=Timin、α=αmin;未知:γ、Udr和Udi。
状态H:已知:α=αs、Id=Id s、Ti=Timax、γ=γs;未知:Tr、Udr和Udi。
通过上面的分析可以知道,如果能确定直流系统运行在哪一状态,就可以确定直流系统的四个直流参数,再增加直流系统的三个独立式(3.48)、式(3.49)和式(3.50),则交直流系统就可以用统一法的思想进行求解。

但是在潮流解算之前,直流系统的运行状态是不确定的,也不能全部确定直流系统的四个参数,所以如何确定直流系统的运行状态成为潮流解算的关键。本书采用的是先假设系统的运行状态,通过对系统潮流试探性的潮流解算来观察潮流的收敛性和潮流迭代结果的合理性,然后判断出直流系统可能处于的运行状态,反复调用相应运行状态的潮流程序进行潮流解算,直到得出满意的潮流计算结果为止。具体的做法如下:
(1)在潮流计算起始时,先假设整流侧和逆变侧的变压器分接头有充足的调节余量,TCC都可以分别控制整流器的触发角α和直流线路电压Ud,这样再加上换流器的控制方程,如整流侧定电流控制Id,逆变侧定熄弧角控制γ,即状态A。可以先进行试探性的潮流计算,如果潮流计算结果收敛并且潮流解合理,那么这个潮流计算的结果可以认为是最终的结果。
(2)如果在潮流解算的过程中,某些待求变量越界,则说明假定的状态并不合理,这时需要通过对越界参数的判断来重新确定已知变量和未知变量。例如,TCC的控制目标是通过对整流侧和逆变侧的变压器分接头的调整分别控制整流器的触发角α和直流电压Ud在合理的范围内,所以在变压器分接头越界时,它就失去了对整流器触发角α或直流电压Ud的控制,这样我们就可以把变压器的变比限定在其所越过的边界值使其成为已知量,如T=Tmin或T=Tmax,而失去控制的整流器触发角α或直流电压Ud则成为新的未知量,通过对直流参数中原有已知变量和未知变量的调整,重新确定直流系统的运行状态,得出一组新的潮流方程,再通过调用相应状态下的潮流程序来完成潮流计算。
(3)在潮流解算的过程中,当同时出现Tr≥Trmax并且α≤αmin时,说明直流系统的运行方式发生了转换,需要在潮流计算中对运行方式进行相应的调整。由于运行方式转换后直流电流由逆变侧电流控制器控制,直流电流整定值为Id=Ids-Im,逆变侧变压器的分接头则不再参与调整,保持原有的值不变,这样再加上Tr=Trmax和α=αmin,则可确定四个直流变量,再由主程序做出判断调用相应状态下的潮流程序来实现。
(4)在迭代收敛,潮流解算完成之后,就可以确定直流系统的全部变量,但在整个潮流解算过程中认为变压器的分接头是连续可调的,而实际上换流变压器分接头是离散调节的。所以在最后要考虑变压器分接头的离散调节问题,重新确定变压器分接头的取值,可用关于变压器分接头离散化的方法进行处理。
(5)通过之前的潮流解算,可以确定直流系统的运行方式,结合在这种运行方式下所确定的直流变量,再对潮流进行一次解算以完成在新变比值下对交直流系统其他变量的调整,最后计算各支路上的功率及平衡节点的功率,输出计算结果。
结合图3.11及前面的分析可以看到,在交直流系统的运行状态发生变化时,直流系统的运行状态有8种,而实际运行中出现的运行状态还可能多于8种,按照前面的方法,每种状态都对应一个潮流的状态方程,这就意味着需要编制8个或者更多的潮流子程序来完成潮流解算。这样做效率低,并且子程序间的转换逻辑的策略过于复杂,这显然是不现实的。
通过观察直流系统的运行状态可以发现,实际上很多状态已知量和未知量是相同的,只是变量的取值不同,如状态B和状态D。这样通过综合比较可以筛选出5个最具代表性的运行状态,各状态及所对应的直流变量如表3.7所示。
表3.7 状态列表
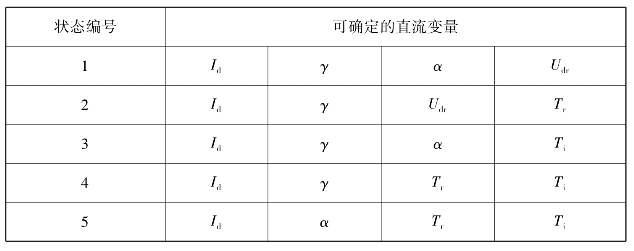
应用时针对不同运行状态对已知变量赋值再调用相应的潮流计算子程序进行潮流解算,计算过程中各状态的判断转换逻辑如下:
(1)若在某种状态下潮流的收敛结果满足(Tr≥Trmax)∪(Tr≤Trmin),对直流变量重新赋值:如果Tr≥Trmax,则Tr=Trmax;如果Tr≤Trmin,则Tr=Trmin,潮流解算转为状态2。
(2)若在某种状态下潮流的收敛结果满足(Ti≥Timax)∪(Ti≤Timin),对直流变量重新赋值:如果Ti≥Timax,则Ti=Timax;如果Ti≤Timin,则Ti=Timin,潮流解算转为状态3。
(3)若在某种状态下潮流的收敛结果满足[(Tr≥Trmax)∪(Tr≤Trmin)]∩[(Ti≥Timax)∪(Ti≤Timin)],对直流变量重新赋值:如果Tr≥Trmax,则Tr=Trmax;如果Tr≤Trmin,则Tr=Trmin;如果Ti≥Timax,则Ti=Timax;如果Ti≤Timin,则Ti=Timin,潮流解算转为状态4。
(4)若在某种状态下潮流的收敛结果满足(Tr≥Trmax)∩(α≤αmin),对直流变量重新赋值:如果Tr≥Trmax,则Tr=Trmax;如果α≤αmin,则α=αmin,潮流解算转为状态5。
本书中,假设潮流计算由状态1开始,则上述转换的逻辑关系可用图3.12表示,如下:
利用前面章节所建立的潮流计算模型结合潮流计算中的状态转换逻辑就可以编写潮流程序来完成基于状态转换的潮流计算。潮流程序由主程序和子程序组成。图3.12中每一个状态都对应着一个潮流子程序,子程序的作用是接收主程序传递来的直流参数,并完成单一状态下的潮流计算,返回计算结果。而直流变量的调整、状态转换的逻辑判断、子程序的调用返回等都由主程序来实现。程序流程图如图3.13所示。

图3.12 状态转换逻辑
该方法可以全面地反映直流系统的调控方式对潮流计算的影响。依据这种方法编写的潮流程序,层次分明,结构清晰。基于状态转换的控制逻辑简单,程序易于实现。状态的转换过程基于子程序调用的方式,在直流系统引入新的控制方式时,只需修改主程序中的转换判断逻辑,程序的扩展性强。
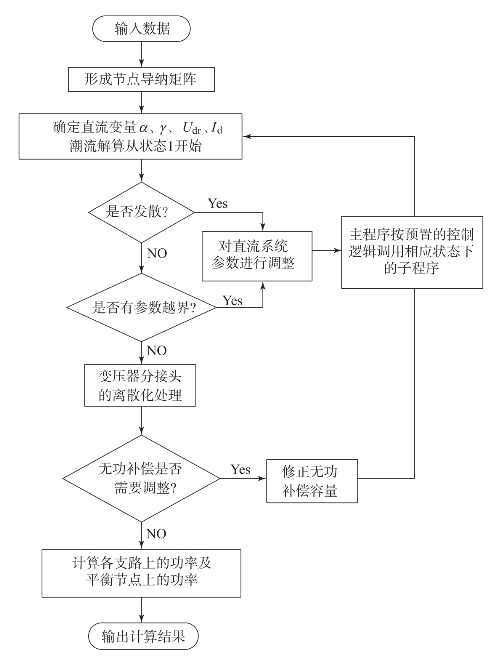
图3.13 潮流程序流程图
有关交直流混合电网计算分析方法的文章

交直流混合系统潮流计算的方法基本上是纯交流系统潮流计算方法的推广,主要有统一迭代法和交替迭代法。由于附加的直流功率项与交流节点参数无关,纯交流系统潮流计算对应部分方程的雅可比矩阵的子矩阵H、N、J和L没有发生变化。有关交直流混合系统功率法方程和矩阵形式,在后续的多端直流潮流计算中还将详细介绍。......
2023-06-29

电压静态稳定性计算与负荷增长方式、电网运行方式和发电机功率增长方式、发电方式和潮流断面增长方式等因素密切相关。本节结合电网运行特点和高压直流输电系统运行特点,在不同的视角下进行交直流电网的电压稳定裕度计算。......
2023-06-29

在美国的第一任房东是一位很难给人留下好印象的女士。认识一个人与认识无人机有着很多相似的地方。然而当我们期望能够深入理解无人机系统时,这些素材就会显得很不全面。本章将围绕下面几个问题来建立对无人机系统更深层次的理解:a.如何完成无人机所需要数据的转换?b.如何实现无人机系统中内外状态的反馈?......
2023-07-05

用牛顿—拉夫逊法进行潮流计算时,节点导纳矩阵的形成、平衡节点和支路功率计算都和运用高斯—塞德尔法时相同,区别仅在于迭代过程。根据式可得式即是用牛顿—拉夫逊法潮流计算时的功率方程。图4-4是牛顿—拉夫逊法潮流计算的流程图。给定值为容许误差ε=10-5试用牛顿—拉夫逊法计算潮流分布。......
2023-06-15

体系转换施工是大沽桥由施工状态向成桥状态转换的重要环节。体系转换主要包括系杆、吊杆的安装及张拉、拱肋支架的拆除、施工平台顶部沙漏的拆除等工作。索支承桥梁结构吊杆的张拉与调整是桥梁设计与施工的关键,关系到施工期和成桥后结构的受力状态及安全性。索力增量与施工顺序无关,只与张拉过程中结构的基本体系有关,而施工张拉力却与施工顺序密切相关。......
2023-07-01

图4-12 调用并传递数据图4-13 调用并传递标识2.功能模块转换策略功能模块转换策略解决如何从数据流程图转换成结构图,有以事务为中心的设计策略和以变换为中心的设计策略两种方法。一般一个模块的扇出系数应该控制在7以内,超过7出错的概率会加大。......
2023-11-23

网络化机组状态在线监测系统通常由传感器、数据采集站、状态数据服务器、WEB服务器、工程师工作站及相关网络设备、软件等组成。通过WEB服务器,机组状态在线监测系统可以在MIS网上发布机组的实时运行状态及历史数据,MIS网上的所有使用者均可以B/S模式和C/S模式对机组数据进行浏览和分析。为充分发挥机组状态在线监测系统的作用,开展远程诊断技术咨询服务是非常必要的。......
2023-06-21

流体流动研究中,研究重点主要在于讨论系统平衡状态随流速的改变情况。系统状态是由系统的性质描述,用来表示系统在当时所处的状况。研究工程热力学、流体力学以及空气动力学等工程问题时,通常是把系统在过程发生的前后平衡状态的改变情况当作问题研究关注的重点。......
2023-06-29
相关推荐