针对交直流混合输电系统的动态稳定性，本节介绍直流输电系统的准稳态模型。准稳态模型对直流系统换流器采用平均值模型，并只对直流输电线和直流控制计及暂态。直流输电系统的基本控制手段就是通过控制这四个变量来满足不同的运行要求。直流输电系统的准稳态模型是一种通用模型，其基本特点是只模拟控制的结果，而不模拟控制系统本身。......
2023-06-29
柔性直流输电系统准稳态模型
【摘要】：近年来，柔性直流输电系统在电网中的应用越来越广泛。在研究包含柔性直流输电系统的动态特性和控制问题中，常采用准稳态模型。直流输电系统内部的动态元件包括VSC直流侧电容以及输电线路的等效电感。式中两端VSC注入直流系统的有功功率计算公式为图2.18双端直流系统内部的动态模型综上所述，构成了用于暂态稳定分析的双端主电路模型。
近年来，柔性直流输电系统在电网中的应用越来越广泛。在潮流计算中，柔性直流输电系统可以等效为四象限功率可控的功率源或负荷，其建模方法可以参考传统直流输电系统。在研究包含柔性直流输电系统的动态特性和控制问题中，常采用准稳态模型。采用该模型时，由于考虑了控制器动态特性，因此仿真的步长通常要比纯交流系统的机电暂态仿真小。采用柔性直流输电系统的准稳态模型的交直流电力系统机电暂态仿真原理如图2.17所示。对直流线路来说，两侧换流器相当于两个电压源，其数值取决于触发控制角和交流侧电压模值，直流线路本身可以采用适当的动态模型[4]。对于直流线路，若不研究直流线路的动态特性，也可以采用集总参数模型。
图2.17 交直流电力系统机电暂态仿真原理
柔性直流输电系统采用准稳态模型，具有以下特点：
（1）换相失败可以比较准确地确定，通过实际计算关断角来确定是否发生换相失败。
（2）直流系统在故障后的恢复过程可以得到较好的模拟，而不是事先指定恢复速度，因为实际的恢复过程必须基于交流电压的恢复过程。
（3）直流系统两个极的控制器是独立模拟的，因而可以模拟直流线路的故障。
（4）由于模拟了定电流、定电压和定关断角等控制器的实际动态过程，因而可以比较准确地模拟直流系统中控制模式的切换过程。
双端直流输电系统内部的动态模型如图2.18所示。图2.18中，Pc1、Pc2以及ud1、ud2分别为VSC1和VSC2注入直流系统的有功功率以及相应直流侧电压；id为直流输电线路上的电流；Cd为直流侧电容；rd、ld则分别代表直流输电线路的等效电阻和电感[4]。
由图2.18可以看出，VSC直流侧电压将直接影响其交流侧的电压输出。因此，在暂态稳定分析中计及直流输电系统的内部动态过程十分必要。直流输电系统内部的动态元件包括VSC直流侧电容以及输电线路的等效电感。如图2.18所示的新型高压直流输电（Voltage Source Converter-High Voltage Direct Current，VSC-HVDC）内部直流系统，对电容电压利用基尔霍夫电流定律，对输电线路电流利用基尔霍夫电压定律，可得双端VSC-HVDC电容电压、输电线路电流的动态方程：
式中，除了Cd、ld、RdB为有效值以外，其余各量均为标幺值。式（2.15）中两端VSC注入直流系统的有功功率计算公式为
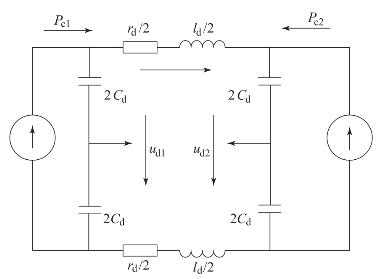
图2.18 双端直流系统内部的动态模型
综上所述，构成了用于暂态稳定分析的双端主电路模型。
VSC能够调节其交流输出电压的幅值与相角，实现对有功功率、无功功率、直流电压以及交流母线电压灵活、快速地控制。VSC-HVDC控制系统均采用比例积分（PI）调节器，有功功率、无功功率、交流母线电压以及直流电压的控制器如图2.19所示，其中Kp、KQ、KU、Ku、TP、TQ、TU、Tu分别为比例积分调节器的比例系数和积分时间常数，TmP、TmQ、TmU、Tmu为测量环节的时间常数，TM和Tδ分别为模拟VSC输出电压幅值和相位调节的时间常数，下标“ref”代表相应物理量的设定值。M0和δ0为稳态运行时的调制比以及相对于交流母线电压相位的移相角度，ΔM和Δδ均为比例积分调节器输出的调节量。另外，控制系统控制的VSC交流侧有功功率Ps以及无功功率Qs计算公式为
VSC-HVDC正常运行时需要有一端VSC采用定直流电压控制，充当整个直流网络的有功平衡换流器，其工作原理如图2.19所示。以定直流电压的VSC向交流系统输送有功功率为例，如果系统扰动引起其直流侧电压升高，负的偏差信号作用于比例积分调节器将使得移相角度的绝对值增大，即换流变压器两端电压的相角差增大。因此，向交流系统输送的有功功率增加，直流电容放电，电压恢复到设定值，其他情况也可做类似的分析。
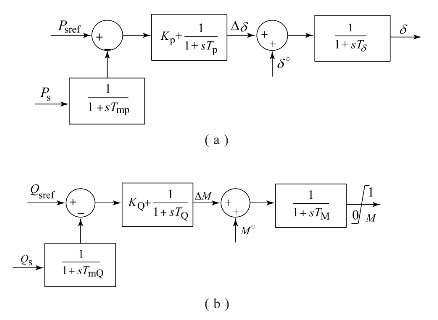
图2.19 基于比例积分调节器的VSC-HVDC主控制系统
（a）有功功率控制器；（b）无功功率控制器
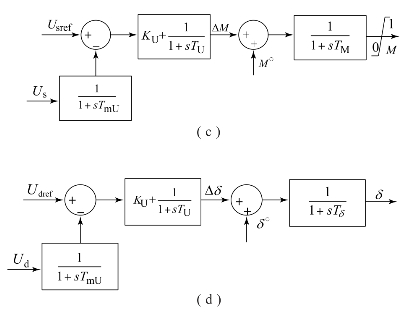
图2.19 基于比例积分调节器的VSC-HVDC主控制系统（续）
（c）交流电压控制器；（d）直流电压控制器
有关交直流混合电网计算分析方法的文章
- 详细阅读
-
直流输电系统稳态模型优化详细阅读
直流输电系统的准稳态模型也是普遍采用的计算模型。图2.6稳态分析时交直流输电系统接口示意图图2.6中，T为换流变压器变比；Pd和Qd分别为注入交流系统的有功功率和无功功率。根据高压直流输电系统的稳态运行等值电路和交直流输电系统接口原理，高压直流输电系统的数学模型如下述方程所示：式中Ut——换流变压器交流母线电压有效值；γ——关断角；μ——换相角。......
2023-06-29
-
基于ADPSS的交直流输电系统的模型优化详细阅读
本节以某特高压直流系统和交流电网组成的交直流混合电网为研究对象，基于混合仿真的基本原理，应用ADPSS搭建特高压交直流系统的机电暂态模型和特高压直流分层接入的电磁暂态模型。图2.22交直流混合电网机电暂态模型表2.1交直流混合电网主要参数2.高压直流系统电磁暂态建模在仿真软件ADPSS中搭建电磁暂态模型，高压直流输电系统包括整流站、两个逆变站、交流滤波器、直流滤波器、平波电抗器、接地极和相应的控制系统。......
2023-06-29
-
多端直流输电系统优化设计详细阅读
多端直流输电系统是由三个及以上换流站，以及连接换流站之间的高压直流输电线路所组成，它与交流系统有三个及以上的接口。由于并联方式具有上述优点，因此目前已运行的多端直流系统均采用并联方式。多端直流输电系统比采用多个两端直流输电系统要经济，但其控制保护系统以及运行操作较复杂。......
2023-06-29
-
直流输电系统结构优化设计详细阅读
图1.1中交流电力系统1和2通过直流输电系统相连。交流电力系统1、2分别是送、受端交流系统，送端系统送出交流电经换流变压器和整流器变换成直流电，然后由直流线路把直流电输送给逆变站，经逆变器和换流变压器再将直流电变换成交流电送入受端交流系统。两端直流输电系统只有一个整流站和一个逆变站，它与交流系统只有两个接口，结构最为简单，是世界上已运行的直流输电工程普遍采用的方式。......
2023-06-29
-
直流与交流输电系统的投资比较详细阅读
而对于交流输电系统而言，虽然无须结构复杂、造价高昂的换流站，但随着输电距离的增加，由于稳定性和过电压等方面的要求，需要另外设置中间开关站。由此可见，直流输电系统中，换流站的投资比重较大，而交流输电系统中，输电线路的投资占主要部分。譬如，直流输电系统中换流站的结构复杂、造价高、损耗大、运行费用高、可靠性较差。......
2023-06-23
-
交直流混合输电系统潮流计算优化方案详细阅读
交直流混合系统潮流计算的方法基本上是纯交流系统潮流计算方法的推广，主要有统一迭代法和交替迭代法。由于附加的直流功率项与交流节点参数无关，纯交流系统潮流计算对应部分方程的雅可比矩阵的子矩阵H、N、J和L没有发生变化。有关交直流混合系统功率法方程和矩阵形式，在后续的多端直流潮流计算中还将详细介绍。......
2023-06-29
-
交直流混合输电系统算例分析详细阅读
交流母线额定电压都为220 kV，直流系统为双桥结构、双极运行，即每个换流站有四个换流变压器。图3.2系统接线图逆变侧换流变压器的参数如下：换流变压器单极容量300 MV·A；变压器漏抗12%；变压器交流侧电压230 kV；直流侧电压96 kV，可计算得出Xci。图3.3潮流计算的收敛特性由图3.3可知，交替迭代计算5次后，交直流系统潮流计算收敛。......
2023-06-29
相关推荐