高斯滤波次数分析的最佳选择

2023-06-29 理论教育版权反馈

【摘要】：本章所提出的方法利用多次高斯滤波来构造原始纹理图像的多尺度图像空间，高斯滤波的次数对本章所提出方法的纹理识别精度和实时性具有重要的影响。从上述两个方面的分析可以看出，过多次数的高斯滤波会导致本章所提出方法的计算量增加和实时性降低。因此，根据表4-1的实验结果及分析，本章方法选择最佳的高斯滤波次数为n=2，此时既能获得最高的纹理识别精度，又能保持较少次数的高斯滤波，从而获得很好的实时性。

本章所提出的方法利用多次高斯滤波来构造原始纹理图像的多尺度图像空间，高斯滤波的次数对本章所提出方法的纹理识别精度和实时性具有重要的影响。如果高斯滤波的次数过少，则不能充分地模拟原始纹理图像的尺度变化，可能会降低算法对尺度变化的稳健性和最终的纹理识别精度；反之，如果高斯滤波的次数过多，则算法的计算量会增加，从而降低算法的实时性，所以必须确定一个最佳的高斯滤波次数，以使本章所提出的方法同时具有较高的纹理识别精度和良好的实时性。考虑到KTH-TIPS纹理库含有丰富的光照、尺度和视角变化，是一个极具挑战性的纹理库，本章选择在KTH-TIPS纹理库上开展实验，分析在不同的高斯滤波次数条件下本章所提出方法的纹理识别精度，以便确定最佳的高斯滤波次数。在开展本实验的过程中，通过改变高斯滤波的次数n，获得对应的纹理识别精度，由于过多次数的高斯滤波会导致算法的计算量增加和实时性降低，本实验仅考虑0～9次的高斯滤波情况，具体的实验结果如表4-1所示。在表4-1中，高斯滤波次数n=0表示没有对原始的纹理图像进行高斯滤波，即没有生成高斯滤波后的图像，多尺度图像空间中只有一个原始的纹理图像。

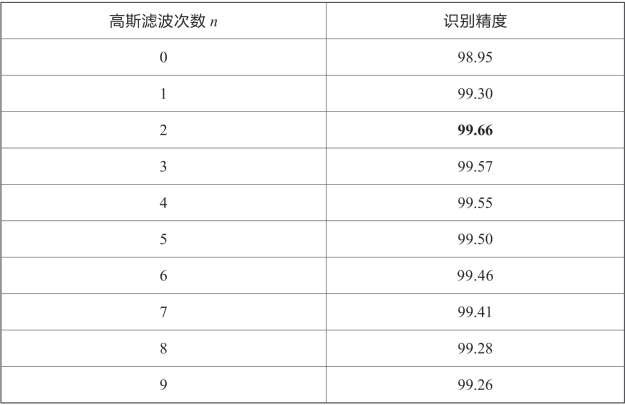
表4-1　不同高斯滤波次数对应的纹理识别精度（%）

pagenumber_ebook=102,pagenumber_book=94

从表4-1可以看出：

（1）当高斯滤波次数n=2时，本章所提出的方法获得了最高的纹理识别精度99.66%，此时多尺度图像空间中包含原始的纹理图像和两次高斯滤波后的图像，用这三个图像即可较好地描述原始纹理图像的尺度变化情况，使本章方法提取的纹理特征对尺度变化具有较好的稳健性，从而获得最高的纹理识别精度。

（2）当高斯滤波次数n<2时，由于没有进行高斯滤波（n=0时）或只进行了一次高斯滤波（n=1时），导致多尺度图像空间中的纹理图像个数过少，不能充分地描述原始纹理图像的尺度变化情况，本章方法所提取的纹理特征对尺度变化的稳健性较差，所以这时的纹理识别精度没有达到最高，即当高斯滤波次数为n=0时本章方法的纹理识别精度为98.95%，当高斯滤波次数为n=1时本章方法的纹理识别精度为99.30%；同时发现，在本章所提出的方法的框架下，虽然在高斯滤波次数n<2时所提取的纹理特征缺乏对尺度变化的稳健性，但仍然保留了对光照条件和图像旋转的稳健性，并且能捕获不同半径R上的宏观和微观的纹理特征。所以，此时本章所提出的方法仍然获得了较高的纹理识别精度（超过98.90%），并且随着高斯滤波次数的增加，本章方法的纹理识别精度呈上升趋势，展现出良好的纹理特征识别能力。

（3）当高斯滤波次数n>2时，本章方法的纹理识别精度开始出现较小幅度的下降，这是因为高斯滤波操作具有对图像的平滑效果，而多次的高斯滤波会使原始的纹理图像过度平滑，丢失了大量的纹理特征，所生成的滤波后图像对原始的纹理特征产生了一定干扰，从而导致本章方法的纹理识别精度下降。但是，当高斯滤波次数n=3～9时，本章方法仍然能够获得很高的纹理识别精度（均超过了99.25%），这表明本章所提出的方法能够提取丰富的、富有鉴别力的纹理特征，使本章方法总能够保持较高的纹理识别精度。

另外，在构建原始纹理图像的多尺度图像空间时，随着高斯滤波次数的增多也会使本章算法的计算量增大，这一方面是因为对纹理图像进行高斯滤波本身就会增加本章算法的计算量，另一方面高斯滤波次数的增加也会生成更多的高斯滤波后图像，而对这些更多个数的高斯滤波后图像提取纹理特征也会增加本章算法的计算量。从上述两个方面的分析可以看出，过多次数的高斯滤波会导致本章所提出方法的计算量增加和实时性降低。因此，根据表4-1的实验结果及分析，本章方法选择最佳的高斯滤波次数为n=2，此时既能获得最高的纹理识别精度，又能保持较少次数的高斯滤波，从而获得很好的实时性。在本章后续对纹理识别精度的分析、对训练样本个数的稳健性分析、对算法实时性的分析等实验中，也同样采用最佳的高斯滤波次数为n=2。

高斯滤波次数分析的最佳选择

相关推荐