实现对尺度变化的稳健性

2023-06-29 理论教育版权反馈

【摘要】：为了使本章所提出的方法能够具备对尺度变化的稳健性，受Harris-Laplace角点检测算法[103]和SSLBP算法[55]的启发，本章采用多尺度高斯滤波模拟尺度变化，然后对联合直方图DDT-CLBPS/M/C跨尺度按直方条取最大值的方法来获得尺度稳健性，其具体的实现过程如下所述。图4-5利用本节所提出的方法实现对尺度变化的稳健性

为了使本章所提出的方法能够具备对尺度变化的稳健性，受Harris-Laplace角点检测算法[103]和SSLBP算法[55]的启发，本章采用多尺度高斯滤波模拟尺度变化，然后对联合直方图DDT-CLBPS/M/C跨尺度按直方条取最大值的方法来获得尺度稳健性，其具体的实现过程如下所述。

1.利用多次高斯滤波构建原始纹理图像的多尺度图像空间

首先，设计如式（4-8）所示的高斯滤波器ga(x,y)，即

pagenumber_ebook=91,pagenumber_book=83

式中：

σ —— 高斯滤波器的标准差。

其次，利用高斯滤波器ga(x,y)对原始的纹理图像I进行n次连续的高斯滤波，每次高斯滤波生成一个滤波后图像，即n次连续的高斯滤波可获得n个滤波图像，最后用原始的纹理图像I和n个高斯滤波图像构建一个多尺度的纹理图像空间，用它描述原始纹理图像I的多尺度特征。

2.计算多尺度图像空间中每个图像的DDT-CLBP特征

在纹理图像I的多尺度图像空间中一共有（n+1）个不同尺度的纹理图像，对每个纹理图像分别按本章4.3.2节提出的方法计算其DDT-CLBPS/M/C联合直方图，并将每个DDT-CLBPS/M/C联合直方图转换成行向量的形式。

3.在多尺度图像空间中跨尺度取DDT-CLBPS/M/C联合直方图特征向量的最大值

对上述第2步生成的（n+1）个DDT-CLBPS/M/C联合直方图行向量，跨尺度对每个直方条取最大值，即取出每个模式的最大值作为该模式的代表值，从而获得一个与DDT-CLBPS/M/C联合直方图特征向量具有相同维数的最大直方图特征向量，将其作为原始纹理图像I对于尺度变化具有稳健性的特征描述。

图4-5展示了利用本节所提出的DDT-CLBP算法实现尺度稳健性的效果。其中，图4-5（a）是同一个纹理类别的两个不同样本，由于受到尺度变化的影响，这两个样本的纹理图像呈现出较大的视觉特征差异；图4-5（b）是利用本节提出的方法提取的DDT-CLBP纹理图像联合直方图特征。从图4-5上下两行图像的对比效果可以看出，虽然图4-5（a）中两个样本的原始纹理图像具有显著不同的视觉尺度特征，但利用本节方法提取的两个样本的DDT-CLBP联合直方图特征具有较高的相似度，如图4-5（b）所示。所以，利用所提取的DDT-CLBP联合直方图特征很容易将两个具有不同尺度和显著视觉特征差异的样本图像判定为来自同一个纹理类别，从而实现正确的纹理图像类别判定。综上所述，本节提出的多尺度高斯滤波和跨尺度取模式最大值的方法能够较好地克服尺度变化对纹理图像识别的影响，从而获得良好的尺度稳健性，其主要原因包括以下两个方面：①多尺度高斯滤波图像能够模拟原始纹理图像的尺度变化情况，从这些图像中能够提取更加丰富、更具鉴别力的纹理特征；②跨尺度取每个模式最大值的方法能够获得每个模式中最显著、最稳定的特征。

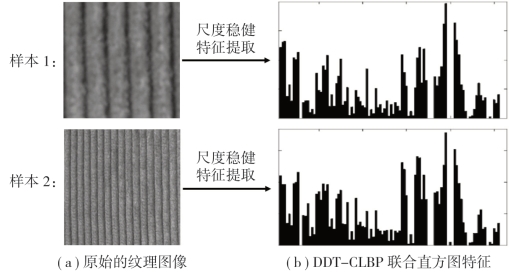
pagenumber_ebook=93,pagenumber_book=85

图4-5　利用本节所提出的方法实现对尺度变化的稳健性

实现对尺度变化的稳健性

相关推荐