如本章前文的分析，VZ-Joint算法所采用的纹理基元的特征维数较高，这导致VZ-Joint算法的纹理基元学习过程和纹理图像编码过程非常耗时，实时性显著下降；而TEISF算法由于采用复杂的纹理基元学习、纹理图像编码和特征生成方法，虽然能够获得较高的纹理识别精度，但该算法的计算量显著增加，导致算法的实时性下降。......
2025-09-29
训练样本个数稳健性分析
【摘要】：表3-3采用不同训练样本个数时的纹理识别精度（%）续表从表3-3可以看出，本章提出的改进Gabor滤波方法对训练样本个数的变化具有更好的稳健性，当训练样本个数不断减少时，本章方法的纹理识别精度下降幅度最小。
为了评估本章所提出的方法对训练样本个数的稳健性，本章在KTHTIPS纹理库上进行实验，分别从每个纹理类别随机选择N = （40， 30， 20，10）个样本作为训练数据，每个纹理类别剩下的（81-N ）个样本作为测试数据，并且将上述对训练数据集和测试数据集的随机划分独立进行100次，每次划分独立进行一次实验，最后计算这100次独立实验结果的平均值，即将平均精度作为最终的纹理识别精度，具体的实验结果如表3-3所示。在此需要说明，对表3-2中列出的很多算法，其对应的原始文献没有开展对训练样本个数的稳健性分析，即没有在文献中报道与表3-3对应的实验结果，这些算法也没有公开发布的源程序代码可利用，很难对这些算法的训练样本个数稳健性进行分析，所以在表3-3中没有列出全部算法对训练样本个数稳健性的分析结果。
表3-3 采用不同训练样本个数时的纹理识别精度（%）
续 表(https://www.chuimin.cn)
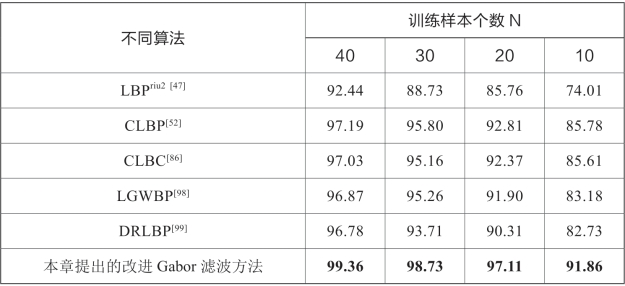
从表3-3可以看出，本章提出的改进Gabor滤波方法对训练样本个数的变化具有更好的稳健性，当训练样本个数不断减少时，本章方法的纹理识别精度下降幅度最小。例如，当训练样本个数N从40降为10时，传统Gabor滤波方法的纹理识别精度从91.48%下降到73.03%，下降幅度达到18.45%，而其他参与对比的算法也都有超过10%的识别精度下降幅度，但本章提出的改进Gabor滤波方法的识别精度从99.36%下降到91.86%，下降幅度仅为7.5%，并且纹理识别精度总保持在90%以上。所以，本章提出的改进Gabor滤波方法具有更好的纹理图像识别能力。
当训练样本个数减少时，本章提出的改进Gabor滤波方法能够获得最高的纹理识别精度，主要原因如下：①本章提出的改进Gabor滤波方法提取的全局Gabor特征和局部Gabor特征均具有很强的鉴别能力，并且通过线性加权求和的方法将这两种Gabor特征进行融合作为最终的纹理图像特征，进一步提高了本章算法的识别能力；②本章提出的改进Gabor滤波方法对每个原始的纹理图像构建了一个多尺度金字塔空间，利用该金字塔空间中四个不同尺度的图像（即一个原始的纹理图像、两个利用采样操作获得的更低分辨率图像、一个利用插值操作生成的更高分辨率图像）来描述原来单一的原始纹理图像，这种方法不但模拟了原始纹理图像的尺度变化情况，使所提取的纹理特征具有更强的尺度稳健性，而且通过采样和插值操作生成了更多个数的纹理图像，弥补了训练样本个数不足的问题，从而减轻了训练样本个数N减小时对识别精度带来的不利影响，使本章所提出的改进Gabor滤波方法仍然能够保持较高的纹理识别精度。因此，和表3-3中列出的其他算法相比，本章所提出的改进Gabor滤波方法具有更好的应用前景，尤其在某些应用场景中可利用的训练样本个数非常有限。例如，在某些危险或人类不方便到达的场景中，能够获取的训练样本个数比较少；在某些医疗场景中，由于获取医疗图像可能会给患者带来检测时的痛苦，能够获取的训练样本个数也会比较少。所以，在这些训练样本个数较少的场景中，本章所提出的改进Gabor滤波方法具有更大的优势，仍然能够获得较好的纹理识别精度。
相关文章
- 详细阅读
-
焊接性的影响因素分析详细阅读
如采用焊前预热和焊后缓冷，可以降低焊缝金属和热影响区的冷却速度，形成塑韧性良好的金相组织，防止出现淬硬组织、降低焊接应力，避免焊缝或热影响区开裂等。接头设计对工艺焊接性的主要影响是：强烈影响焊缝金属和热影响区的冷却速度；决定冷却和收缩时的应力分布。......
2025-09-29
-
钎料润湿性影响因素分析详细阅读
由杨氏方程可知，任何使三相表面张力发生变化，从而使接触角θ发生变化（减少）的因素都将影响钎料对母材的润湿性。从物理意义上说，如使σLV减小，意味着液体内部原子对表面原子的吸引力减弱，液体原子容易克服本身受到的引力趋向液体表面，使液体的表面积增大，钎料容易铺展。而σSV增大，说明固体的内部原子对表面原子的吸引力增大，表面原子处于高能态。......
2025-09-29
-
涂层磨粒磨损性试验分析详细阅读
磨粒磨损有三种形式。3）外界磨粒移动于两摩擦表面之间，类似于研磨作用，称为三体磨粒磨损。表5-11 磨粒磨损试验条件耐磨性评价 根据涂层的失重量情况，评价其耐磨性。试验设备及试验条件 试验机为国产销盘式ML-10型磨粒磨损试验机。图5-24 销盘式磨粒磨损试验1—垂直轴 2—金属圆盘 3—砂布（纸） 4—试样 5—夹具 6—载入砝码表5-12 销盘式磨粒磨损试验条件......
2025-09-29
-
土壤导电性与腐蚀性的关系分析详细阅读
土壤的导电性土壤的电阻率与土壤的腐蚀性有密切的关系。显然这一关系是由土壤腐蚀的电化学性质决定的。表2-5土壤电阻率与腐蚀性的关系土壤的导电性主要取决于下列条件：1）土壤的含水量。土壤中可溶性盐类全部溶解时，金属腐蚀速度将达到最大值。当温度升高至25～30℃时，最适宜细菌生存、繁殖，也会加剧土壤腐蚀。埋在贫氧黏土段的管段成为阳极，发生严重的局部腐蚀。由杂散电流引起的腐蚀称为杂散电流腐蚀。......
2025-09-29
-
柴油机热流相关性分析及实验结果分析详细阅读
柴油机的热流测量方法与汽油机类似。柴油机也同样表现为每个循环的热流曲线之间有很大的变化。试验条件是压缩比为16，转速为2000r/min，当量比为φ=0.5，进气系统压力为1.5×105Pa。图8-20 中间涡流柴油机热流涡流较小的柴油机活塞凹部的平均热流通常比活塞冠部环状壁部位和气缸盖部位的平均热流高。图8-21 自然进气柴油机的气缸盖与气缸套处热流Praum计算求出活塞壁面与气缸盖面的热传递率h1，以及气缸套面的热传递率h2，并比较判定后者为前者的1/3，即h2=1/3h1......
2025-09-29
-
气缸端盖密封性分析详细阅读
由于结构限制，气缸与前后端盖之间无法使用垫片来保证密封，只能通过施加合适的螺栓预紧力使气缸与端盖之间产生一定接触压力以确保密封。因此主要分析此工况下气缸与端盖的密封状况。但过大的螺栓预紧力会使发动机发生过大的变形，过多的螺栓会削弱结构的强度，因此需要合理地进行结构改进。可以通过增加螺栓个数或增大螺栓预紧力来改善这部分区域的密封性能。......
2025-09-29
-
推进性能优化及环境适应性分析详细阅读
推进原理的详细内容已在12.1.1一节中进行了说明。火箭发动机运行时，随高度变化的环境大气压力p3发生变化时，其推力也发生变化。压力推力与环境大气压力p3有关，因大气压p3随高度的增加而减小，因此火箭发动机的推力F与比推力Is随着高度的增加而增大。图13-21 随高度的火箭发动机推力和比推力2.有效排气速度有效排气速度c（m/s）定义为火箭发动机的推力F与推进剂的质量流量率之比。......
2025-09-29
相关推荐