现有的图像检索方式主要分为两种:基于文本的图像检索和基于内容的图像检索。针对以上两点问题,本书对局部特征提取技术和相关反馈技术进行了深入的研究分析,提出了一种基于局部特征的图像检索方法。......
2025-09-29
传统的Gabor滤波方法和最近提出的LGWBP算法在纹理图像识别上的性能不够理想,主要是因为上述方法都只利用了Gabor滤波后的幅值图像,尤其传统的Gabor滤波方法只利用滤波后幅值图像的均值和标准差作为所提取的纹理特征,这种特征表示过于粗略,未能充分描述原始纹理图像的特征,自然很难获得满意的纹理图像识别精度。本章在研究中发现,除了Gabor滤波后的幅值图像具有重要的纹理信息,Gabor滤波后的相位图像也含有鉴别性的纹理特征,尤其当Gabor滤波后的幅值图像和相位图像以成对组合的形式出现时,能够实现Gabor滤波后幅值图像和相位图像的特征融合,在这种情况下提取的纹理特征具有更强的鉴别能力,预计能够进一步提高纹理图像的识别精度。图3-2展示了一幅原始的纹理图像及其对应的Gabor滤波后的一组幅值图像和相位图像,对比三个图像可以看出,Gabor滤波后的幅值图像和相位图像都含有重要的纹理特征,它们都可用于纹理图像的特征提取和识别任务。

图3-2 Gabor滤波后的幅值图像和相位图像
综上分析,为了进一步挖掘Gabor滤波方法在纹理图像特征提取和识别领域的潜力,本章提出一种改进的Gabor滤波方法,即金字塔空间中全局和局部编码Gabor特征融合的纹理图像特征提取和识别方法。该方法的基本原理如图3-3所示。
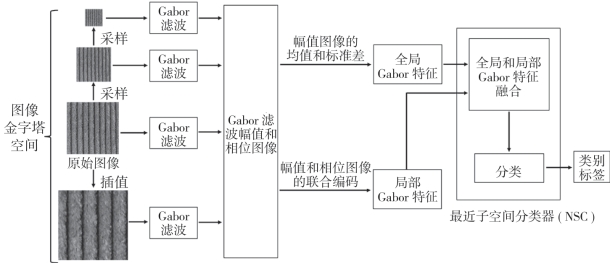
图3-3 本章提出的改进Gabor滤波方法的原理图
本章所提出的改进Gabor滤波方法的具体实现过程如下所述。
(1)为原始的纹理图像构造多尺度金字塔空间。获取图像时相机与纹理样本的距离远近不同,这会导致所获取图像中样本的尺度发生变化,而不同尺度的纹理图像可能会呈现显著的视觉特征差异,这给纹理图像的特征提取和识别带来了很大的挑战。因此,为了克服纹理图像的尺度变化,本章利用采样和插值的方法构造一个多尺度的金字塔空间,用于模拟每个样本图像的尺度变化情况。图3-4展示了利用金字塔空间模拟纹理图像尺度变化的效果,其中第一行是实际拍摄的一组具有不同尺度特征的纹理样本图像,从左到右的图像尺度逐渐变小,从这些图像可以看出,由于相机与样本的距离远近不同,这些不同尺度的样本图像所体现出的视觉纹理特征存在很大的差异;第二行是利用多尺度金字塔空间模拟出的具有不同尺度的纹理图像。通过对比第一行的实际拍摄图像和第二行的多尺度模拟图像,可以看出利用多尺度的图像金字塔空间能够较好地模拟现实中拍摄的纹理图像的尺度变化情况。因此,本章为每个原始的纹理图像构造多尺度的金字塔空间,然后对金字塔空间中不同尺度的所有图像进行特征提取和分析,这样就能够获得对图像尺度变化的稳健性。

图3-4 利用金字塔空间模拟纹理图像的尺度变化
在构建纹理图像的多尺度金字塔空间时,为了获得较连续的尺度变化和较高的算法实时性,本章设图像采样和插值的比率都为2,即图像采样时从每两个像素点中采样一个像素点,插值时在两个像素点之间插入一个像素点。为了确定合理的金字塔空间的层数,本章方法主要考虑以下两个因素:①很多纹理图像的尺寸比较小(如128×128),过多次数的采样操作会使图像变得很小,几乎不再含有有用的纹理特征,对纹理图像的特征提取和识别没有意义,因此本章设采样的次数为2,即对原始的纹理图像连续采样两次,每次采样生成一个更低分辨率的纹理图像,从而获得两个低分辨率的纹理图像,将这两个采样生成的图像分别作为多尺度金字塔空间中的两层图像。②图像插值是非常耗时的操作,因为在确定一个插值像素点灰度值的过程中需要计算附近多个像素点的灰度值,所以为了保持本章所提出算法的实时性,在本章算法中设插值操作的次数为1,即仅利用插值操作生成一个更高分辨率的图像。同时,为了获得好的实时性,本章算法采用速度最快的最近邻插值方法(即把最近邻像素点的灰度值作为插值点像素的灰度值),并且只截取原始纹理图像中心的1/4区域进行插值,其他的3/4区域舍去不用。按照上述方法对原始的纹理图像进行两次采样和一次插值操作之后,一个原始的纹理图像对应的多尺度金字塔空间一共有四层,分别对应四个不同尺度的纹理图像,其中一个是原始的纹理图像、两个是利用采样操作生成的低分辨率图像、一个是利用插值操作生成的高分辨率图像,这四个图像构成一个原始纹理图像的多尺度金字塔空间,在特征提取和识别过程中用于描述一个原始纹理图像的多尺度特征。
(2)设计合理的Gabor滤波器组,并对金字塔空间中的纹理图像进行Gabor滤波。从信号处理的角度来看,Gabor滤波方法是把不同尺度的纹理图像特征视为位于不同频率位置的窄带信号,因此可设计一组具有不同中心频率和带宽的滤波器组,并利用这个滤波器组来提取这些具有不同中心频率和带宽的窄带信号纹理特征。在使用Gabor滤波方法进行纹理图像的特征提取和识别时,必须首先设计一个合理的Gabor滤波器组,这个Gabor滤波器组可以通过对一个基本的Gabor小波在不同的尺度进行伸缩并在不同的角度进行旋转来获得。Gabor滤波器组是非正交的,这导致在不同的尺度和方向上所提取的纹理特征之间存在大量的冗余信息,所以在设计Gabor滤波器组时,既要考虑能够充分提取不同尺度和方向上的纹理特征,又要考虑能够有效降低在不同尺度和方向上所提取纹理特征的冗余度。因此,本章采用Manjunath和Ma提出的Gabor滤波器组设计方法[82],该方法使Gabor滤波器组的频域响应在半峰幅值处相切,即刚好接触且没有混叠,这样既能覆盖尽可能多的频域范围,以便更加充分地提取各个频段的纹理特征,又不引入冗余信息,从而能够有效地提取纹理特征。在利用上述方法设计Gabor滤波器组时,根据其设计准则可确定Gabor滤波器组在频率域的标准差参数σu和σv,即可根据式(3-3)、(3-4)、(3-5)来计算参数σu和σv,如下所示

式中:
Fh —— 在纹理图像中感兴趣的最大中心频率;
Fl —— 在纹理图像中感兴趣的最小中心频率;
S —— 待提取特征的总的尺度个数;
K —— 待提取特征的总的方向个数。
在设计上述Gabor滤波器组之后,一共获得在S个尺度和K个方向上的S×K个滤波器,然后利用这个滤波器组对金字塔空间中的每个纹理图像进行Gabor滤波,可获得在不同尺度和方向上的Gabor滤波图像,其卷积滤波过程可用式(3-6)表示,即
![]()
式中:
I(x ,y) —— 金字塔空间中的一个灰度纹理图像;
gs,k(x, y) —— Gabor滤波器组中在尺度s、方向k上的Gabor滤波器;
—— 卷积滤波运算;
Ws,k(x ,y) —— 在尺度s、方向k上的Gabor滤波后图像。
(3)提取Gabor滤波后图像的全局Gabor特征。对于一个原始的纹理图像,它在金字塔空间中一共有4个对应图像(即一个原始的纹理图像,两个利用采样操作获得的更低分辨率图像,一个利用插值操作生成的更高分辨率图像),在利用Gabor滤波器组中的S×K个Gabor滤波器分别对金字塔空间中的每个图像进行卷积滤波之后,一共可获得4×S×K个滤波后图像。对这些滤波后的图像分别计算幅值图像,再计算幅值图像的均值和标准差,然后把每个尺度和方向上的均值和标准差级联,如式(3-7)所示,将其作为原始纹理图像的全局Gabor特征,即
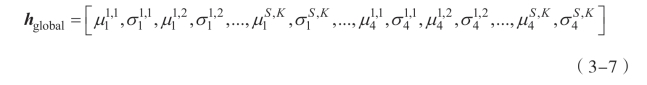
式中:
µis,k —— 金字塔空间中的第i个图像,利用Gabor滤波器组中在尺度s、方向k上的Gabor滤波器对其进行卷积滤波,获得滤波后幅值图像的均值;
σis,k —— 金字塔空间中的第i个图像,利用Gabor滤波器组中在尺度s、方向k上的Gabor滤波器对其进行卷积滤波,获得滤波后幅值图像的标准差。
需要说明的是,按上述方法提取的全局Gabor特征是建立在传统Gabor滤波方法的基础之上的,即提取了Gabor滤波后幅值图像的均值和标准差,但本章所提出的方法又与传统的Gabor滤波方法存在不同之处,传统的Gabor滤波方法只利用一个原始的纹理图像提取滤波后幅值图像的均值和标准差作为特征描述,而本章提出的方法先为每个原始的纹理图像构建了一个多尺度的金字塔空间,然后用多尺度金字塔空间中四个不同尺度的纹理图像与Gabor滤波器组进行卷积,最后将提取滤波后幅值图像的均值和标准差作为全局的Gabor特征。通过上述分析可以看出,传统的Gabor滤波方法只利用一幅原始的纹理图像提取全局的Gabor特征,而本章提出的方法利用四个不同尺度纹理图像的特征作为全局的Gabor特征,因此本章方法提取的全局Gabor特征包含更多的纹理信息,尤其对纹理图像的尺度变化具有稳健性,所以当待识别的纹理图像存在尺度变化时,本章方法的识别性能将优于传统的Gabor滤波方法。
(4)提取局部的Gabor特征,即Gabor滤波后幅值图像和相位图像的联合编码特征。上述步骤所提取的全局Gabor特征只能描述纹理图像的整体性特征(即均值和标准差都属于全局特征),这种描述过于粗略,无法体现纹理图像在细微特征上的差别。例如,有很多纹理图像虽然具有相同的全局特征(即整幅图像的均值和标准差相同),但由于它们具有不同的局部特征(如所含纹理基元的排列规律不同)而属于不同的纹理类别,这时仅利用全局的Gabor特征就无法对这些纹理图像进行有效的鉴别,从而造成纹理识别的错误结果。因此,除了全局特征,不同类别的纹理图像在局部特征的分布上可能存在更加明显的差异。例如,两个不同类别纹理图像的均值和标准差可能相同,但图像中纹理基元的形状、尺寸、个数、排列规律等都可能不相同,所以仅利用全局的Gabor特征无法对其进行有效识别,这时利用纹理图像的局部特征进行鉴别将更加有效。另外,本章在研究中发现,Gabor滤波后的幅值图像和相位图像都含有有用的纹理特征,即Gabor滤波后的幅值图像和相位图像都可以在纹理图像的特征提取和识别任务中发挥自己的作用,尤其当Gabor滤波后幅值图像和相位图像按成对组合的形式同时出现时,能够有效实现Gabor滤波后幅值图像和相位图像的特征融合,此时提取的Gabor融合特征将具有更强的鉴别能力。因此,根据上述特征融合的思想,本章提出一种Gabor滤波后幅值图像和相位图像联合编码的方法,以便从Gabor滤波后的幅值图像和相位图像中提取更具鉴别力的局部Gabor特征。
本章方法提取局部Gabor特征的具体步骤如下。
步骤1:计算所有尺度和方向上每个Gabor滤波图像的幅值分量和相位分量,即
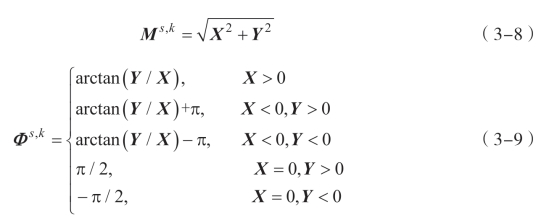
s=1,2,,S k=1,2,,K
式中:(https://www.chuimin.cn)
X —— 在尺度s、方向k上,Gabor滤波图像的实部分量,即Re{W s,k};
Y —— 在尺度s、方向k上,Gabor滤波图像的虚部分量,即Img{W s,k};
Ms,k —— 在尺度s、方向k上,Gabor滤波图像的幅值分量;
Φs,k —— 在尺度s、方向k上,Gabor滤波图像的相位分量。
上述式(3-8)、(3-9)所示的计算过程都是按像素进行的,相位分量的取值范围是[−π,π]。在获得Gabor滤波后的幅值分量和相位分量之后,还需要对每个Gabor滤波图像的幅值分量和相位分量进行归一化,即

s=1,2,,S k=1,2,,K
步骤2:对每个Gabor滤波图像的幅值分量和相位分量分别进行8位联合编码。其中,Gabor滤波图像的幅值分量作为高4位编码,Gabor滤波图像的相位分量作为低4位编码,从而构建一个8位的联合编码。具体来说,就是先将归一化的Gabor滤波幅值分量和相位分量分别量化成16个等级,其量化范围均为[0, 15],然后按照式(3-12)所示的方法计算幅值分量和相位分量的联合编码图像,即
![]()
式中:
Mqs,k —— 在尺度s、方向k上,16个等级量化后的Gabor滤波幅值分量;
Pqs,k —— 在尺度s、方向k上,16个等级量化后的Gabor滤波相位分量;
Js,k —— 在尺度s、方向k上,16个等级量化后幅值分量和相位分量的联合编码图像。
从上述计算过程可以看出,Gabor滤波后幅值分量和相位分量联合编码图像的取值范围是[0, 255]。
步骤3:对每个尺度s、方向k上的幅值和相位联合编码图像Js,k计算直方图,并表示为hs,k,因为联合编码图像的取值范围是[0, 255],所以该直方图是一个256维的特征向量,可用这个直方图表示在尺度s、方向k上提取的纹理特征。然后,按照式(3-13)的方法对同一个尺度上所有K个方向的直方图向量按对应直方条的方式取最大值,即
![]()
用获得的特征向量hs描述一个纹理图像在Gabor滤波后一个尺度上的局部特征。
步骤4:将一个纹理图像在S个尺度上的最大直方图(行向量形式),然后按式(3-14)的方法进行级联,可获得一个包含多尺度信息的直方图行向量,即

下标i表示多尺度金字塔空间中第i层的图像,即hi表示多尺度金字塔空间中一个图像的直方图特征向量,可用它描述第i个纹理图像的特征。
步骤5:对于一个原始的纹理图像,它的多尺度金字塔空间一共含有4个图像(即一个原始的纹理图像,两个利用采样操作获得的更低分辨率图像,一个利用插值操作生成的更高分辨率图像),这4个纹理图像对应有4个直方图向量hi(i=1,2,3,4),把这4个图像的直方图向量hi按直方条的方式再取最大值,可得

最后,将获得的直方图向量hlocal作为原始纹理图像的最终局部Gabor特征。
(5)全局Gabor特征与局部Gabor特征的融合以及最终的纹理类别判定。全局Gabor特征hglobal体现了纹理图像的整体性特征,局部Gabor特征hlocal体现了纹理图像更具体的局部特征,两者对纹理图像的特征提取和识别都具有重要作用。因此,为了充分利用全局Gabor特征和局部Gabor特征中的鉴别性信息,本章方法采用在NSC分类器的框架下对这两种特征进行融合,并将融合后的Gabor特征用于纹理图像识别。具体的实现过程如下所述。
在NSC分类器[55]的框架下,设一共有C类纹理,每个纹理类别有n个训练样本,把这n个训练样本的全局Gabor特征均转换为列向量,即每个训练样本的全局特征作为一个列向量,然后将这些列向量按列放置可组成一个如式(3-16)所示的矩阵,用这个矩阵表示该类纹理的全局Gabor特征子空间,即
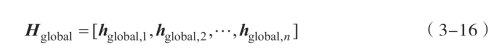
按照相同的方法,把这n个训练样本的局部Gabor特征也转换为列向量,然后分别按列放置可组成一个如式(3-17)所示的矩阵,用这个矩阵表示该类纹理的局部Gabor特征子空间,即

![]()
上标T表示矩阵的转置操作。
然后,分别计算测试样本y的全局Gabor特征和局部Gabor特征在每个纹理类别特征子空间中的投影残差,即

为了同时获得好的特征鉴别能力和实时性,本章采用简单高效的加权平均方法将全局Gabor特征的投影残差errglobal和局部Gabor特征的投影残差errlocal进行特征融合,即
![]()
其中,加权参数w的值可以通过实验来确定。
最后,计算测试样本y在所有纹理类别的投影残差,并将测试的纹理样本划分到投影残差最小的那个纹理类别,从而实现测试样本的纹理类别判定,即
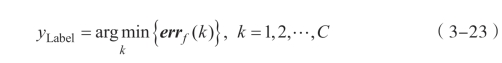
相关文章

现有的图像检索方式主要分为两种:基于文本的图像检索和基于内容的图像检索。针对以上两点问题,本书对局部特征提取技术和相关反馈技术进行了深入的研究分析,提出了一种基于局部特征的图像检索方法。......
2025-09-29

航拍图像拼接技术是当前机器视觉领域的一个研究热点,已经被广泛应用于地理信息系统、地质灾害监测、城市规划和战场态势评估等许多方面。但是,由于是在飞行器上对地面场景的俯视拍摄,所以又有其自身的特点和难点,比如飞行器姿态变化导致的航拍视角改变、飞行器升降造成的图像分辨率不同、天气状况对图像质量的影响等。该方法比较适合于全景图像拼接。......
2025-09-29

3)按Ctrl+B组合键,隐藏叶片背面型线,这时图形窗口中只显示叶片工作面“blade_p”的曲线组。图2.9-7 创建导叶叶片背面曲面3.完成叶片表面曲面的创建显示设置隐藏所有的曲线,只显示叶片工作面和背面曲面。扩大曲面为防止后面切割叶片时,曲面切割不到,故需扩大工作面和背面。图2.9-8 导叶叶片曲面的扩大4.创建叶片的其他曲面1)在菜单栏中,选择→→或单击工具栏的“通过曲线组”按钮,弹出“通过曲线组”对话框。......
2025-09-29

同样地,据日本三菱化工机械公司对10年中化工设备破坏事故的调查统计表明:均匀腐蚀仅占8.5%、应力腐蚀占45.6%、孔蚀占21.6%、腐蚀疲劳占8.5%、晶间腐蚀占4.9%、高温氧化占4.9%、氢脆占3.0%,由此可见局部腐蚀的严重危害性。......
2025-09-29

同时,Gabor滤波方法具有时域和频域的联合最佳分辨率,能达到时频测不准的下界[83],因此能很好地实现多分辨率的时频分析。图3-1Gabor小波的尺度和方向选择特性由于Gabor小波具有良好的视觉仿生学性质,能够捕获纹理图像中多个尺度和方向的纹理特征,Gabor小波在纹理图像的特征提取和识别领域具有独特的优势,受Gabor小波良好性质的启发,研究人员提出了一系列基于Gabor滤波的纹理图像特征提取和识别方法。......
2025-09-29

Zhong Ning等人提出了一种基于距离的全局特异数据挖掘的构架[101]。其中,Mj和σj分别代表aj所有PF值的均值和标准差。Pr=RPF均值+γ×RPF的标准差(3.4)可以看出,此构架是基于距离的,并且找到的特异数据是全局的。从式(3.1)得出,属性xij和xkj间的距离d是后续计算的基础。由前述可知,此构架可以处理各类属性值,并且可以处理多个相关数据集的特异挖掘问题。......
2025-09-29

反映水库工作状况的水位,称为水库的特征水位,与特征水位相应的库容称为水库的特征库容。正常蓄水位是水库最重要的特征水位之一。防洪高水位至防洪限制水位之间的库容称为防洪库容。图G4.7水库特征水位与特征库容示意图6.校核洪水位(Z校)和校核洪水调洪库容(V调校)当水库遇到大坝校核标准的洪水时,水库坝前达到的最高洪水位,称为校核洪水位。......
2025-09-29

特征选择的方法按照特征选择过程与分类器之间的交互程度可以分为过滤式、Wrapper[73]、嵌入式、混合式几种类型。在Wrapper方法中,特征子集的性能使用一个分类器在验证样本上的正确率来衡量,这样选择的特征比较适合该分类器,但不一定适合其他的分类器。由于在特征选择过程中要评价很多特征子集,即使采用顺序前向搜索,Wrapper方法的计算量都是很大的,只适合特征维数不太高的情况。......
2025-09-29
相关推荐