纹理特征研究的历史与现状

人类对纹理特征的研究最早可追溯到1962年Julesz[44]对纹理视觉感知模型的研究，时至今日，人们对纹理图像的研究已经有50多年的历史。在这50多年里，人们对纹理图像的认识和理解不断深入，提出了各式各样的纹理图像特征提取和识别算法，这些算法也在实际生活中获得了广泛的应用。目前，对纹理图像特征提取和识别方法的研究比较深入的团队有牛津大学工程科学系的视觉几何研究组VGG（Visual Geometry Group， Department of Engineering Science， University of Oxford）[45，46]、奥卢大学的机器视觉研究组MVG（Machine Vision Group， University of Oulu）[47-51]等。在国内，清华大学的郭振华[52-57]、国防科技大学的刘丽[1，2， 58-61]、重庆邮电大学的宋铁成[62-64]等也在该方面进行了深入的研究。

20世纪60年代，人们对纹理图像的研究还处于萌芽阶段，主要成果如下：①1962年，Julesz对纹理的视觉感知模型进行了初步研究；②1966年，Brodatz为艺术家和设计人员创建了一个纹理图像摄影集（Brodatz纹理库）[65]，这成为人们最初研究纹理的重要图像来源。

20世纪70年代，最具代表性的纹理图像特征提取和识别方法是灰度共生矩阵（Gray Level Co-occurrence Matrix， GLCM）方法[66]，它是由Haralick于1973年首次提出的，这种方法提取的纹理特征对规则的纹理图像具有较好的识别效果。因为纹理图像是由灰度分布在空间位置上反复出现而形成的，所以相隔一定距离的两像素之间会存在一定的相关性和共生性，GLCM方法就是通过检测灰度的空间共生性来描述纹理图像的特征的。GLCM方法的基本原理是对某个距离d和某个方向θ上灰度级为(i,j)的像素出现的次数进行统计，从而构造一个GLCM矩阵，但二维的GLCM矩阵不方便直接用于纹理图像的特征描述和分析上，所以利用这个GLCM矩阵计算一组特征量，再用这组特征量来描述纹理图像的特征并用于纹理图像识别。图1-7展示了当选择距离d=1、方向θ=0°时根据输入图像计算GLCM矩阵的基本原理。不同的距离d和方向θ对应不同的共生矩阵和特征量，从而能够描述纹理图像在不同距离和不同方向上的灰度共生性质。通常情况下，距离可选d=1～5，方向可选θ=0°, 45°, 90°,135°。Haralick提出从共生矩阵中计算14个特征量[66]，包括角二阶矩（Angular Second Moment）、对比度（Contrast）、相关值（Correlation）、方差（Variance）、逆差矩（Inverse Diference Moment）、和平均（Sum Average）、和方差（Sum Variance）、熵（Entropy）、差熵（Difference Entropy）、和熵（Sum Entropy）等，但这些特征量存在相关性，即提取的纹理特征存在冗余，因此常选用其中的4个特征量（角二阶矩、对比度、熵、相关值）作为纹理特征的描述，原因是这4个特征量的描述能力强，并且相关性低。

图1-7　计算GLCM矩阵的基本原理

GLCM方法的不足之处主要有以下两点：①计算量大。灰度图像通常有Ng=256个灰度等级，则一个共生矩阵的维数高达Ng×Ng=256×256=65 536，并且通常需要计算多个距离d和多个方向θ的共生矩阵，这使GLCM方法非常耗时。为了解决这个问题，通常采用量化的方法降低原始图像的灰度等级个数。例如，将原始图像量化为32或16个灰度等级，则GLCM方法的计算量会大大降低。②GLCM方法提取的纹理特征对人工合成的纹理图像具有较好的识别效果，因为很多自然纹理图像都存在不规则性和随机性，所以GLCM方法的识别效果较差。

20世纪80年代，马尔可夫随机场（Markov Random Field， MRF）方法和分形维（Fractal Dimension）方法成为研究的热点。MRF方法[67-70]是把纹理图像视为一个随机的二维图像场，并且假定每个像素的灰度值仅与周围像素的灰度值有关，即把纹理图像构建为一个二维的MRF模型。MRF模型的参数能够描述纹理图像中聚类的强度和方向，这使纹理图像的特征与MRF模型的参数相对应。因此，在MRF方法中，纹理图像的特征提取过程就是对MRF模型参数的估计过程，可用估计的MRF模型参数来描述纹理图像的特征。MRF方法实际是将传统信号分析中的二维随机过程应用于纹理图像的特征描述，该方法能取得不错的纹理识别效果。MRF方法的不足之处主要有以下几点：①MRF方法假定纹理图像的灰度分布符合MRF模型，但这个假设在实际中不一定成立，因为很多纹理图像无法仅用一个单一的MRF模型来描述；②MRF模型仅考虑每个像素与其邻域像素的依赖关系，缺乏对图像整体纹理结构特征的描述；③MRF模型的参数求解存在一定难度，并且计算量大；④为了获得好的参数估计值，需要纹理图像的尺寸足够大。

分形维方法[71-74]主要是针对纹理图像中不同尺度的纹理基元的结构形态进行研究，是一种结构分析方法。在欧氏空间中，人们常认为点是零维的，线是一维的，面是二维的，体是三维的。和欧氏空间中的整数维（0、1、2、3）不同，分形维数的值通常不是整数，而是分数。Pentland[71]证明了图像的分形维数与图像的粗糙度具有相关性：分形维数越小，对应的图像越光滑；分形维数越大，对应的图像越粗糙。因为纹理图像在不同的尺度上具有自相似性和不同的粗糙度，所以可利用分形维数来描述纹理图像的粗糙程度，把分形维数作为纹理图像的特征参数，用于纹理图像的识别。计算一幅纹理图像的分形维数，常用的方法是盒计数法（Box-counting Method）[72]，其原理是用边长为r的正方形盒子把被测形体覆盖起来，用N(r)表示所需的盒子个数，当盒子的边长r变小时，N(r)会增大，则图像的分形维数可定义为

例如，覆盖一个单位长度的线段需要N (r)=1/r ，覆盖一个单位长度的正方形需要N (r)=(1/r )2，覆盖一个单位长度的立方体需要N (r)=(1/r)3，其幂次就体现了线段、正方形、立方体的分形维数，即D=1，2，3。其他的例子还有，科赫曲线的分形维数是D=1.261 8，谢尔宾斯基海绵的分形维数是D=2.726 8。在实际计算分形维数时，通过改变r的值，可获得不同尺度下的多个样点(r,N(r))，将这些样点在log坐标系中拟合成一条直线，最后用拟合直线的斜率作为分形维数的近似值。

分形维方法的主要优点有：①分形维数能描述纹理图像的粗糙程度，这与人类对纹理图像粗糙程度的视觉感知是一致的；②分形维数具有一定程度的尺度不变性、抗噪性以及旋转不变性；③分形维数能够体现不同尺度之间的自相似性。但是，分形维方法也存在明显的不足之处，即分形维数只能度量纹理图像的粗糙程度，考察特征过于单一，很多不同类别的纹理图像虽然在视觉特征上存在较大差异，但由于整体的粗糙程度相似，其分形维数非常接近，从而很难利用分形维数将这些不同类别的纹理图像区分开来。所以，分形维方法提取的特征信息比较单一，鉴别能力有限，之后很少有学者对这种方法继续进行研究。

20世纪90年代，以小波变换[75-77]为核心的多分辨率分析方法成为研究的潮流。心理物理学的研究表明，人类的视觉系统在处理纹理图像时，常将图像分解为不同频率和方向上的信号进行分析，这与小波变换所具有的信号多分辨率分析能力相对应。利用小波变换提取纹理图像特征的过程主要如下：首先选择一个合适的小波基，其次利用小波变换将纹理图像分解到具有不同频率和方向的多个子带上，并从每个子带提取鉴别性的特征（如每个子带的能量均值和方差），最后将这些特征作为纹理图像的多尺度特征描述子。传统的小波变换每次仅对低频子带进行分解，对图像的低频信息利用比较充分，但纹理图像的高频子带也含有重要的纹理信息。为了解决这个问题，人们提出了小波包变换[78]、双树复小波变换[79]等方法，能够同时对低频和高频子带进行分解，从而获得了更加丰富的多尺度纹理特征。小波变换方法的优点是能够对纹理图像进行多分辨率分析，以获得不同尺度和方向上丰富的纹理特征，但小波变换方法也存在一些不足之处：①在进行小波变换时，小波基的选择对纹理特征的提取至关重要，会影响纹理图像特征描述的质量，但现实中纹理图像的形态复杂多样，目前还没有好的方法能够针对不同的纹理图像自适应地选择最佳的小波基；②对图像进行多层小波变换时，计算量也比较大；③小波变换仅对图像在水平、垂直和对角线这三个方向进行分解，方向选择的灵活性和精度不足。

Gabor滤波方法[80-82]也是一种常用的纹理图像特征提取方法，它与小波变换方法有相似之处，两者都能对图像进行多分辨率分析，因此有时也被称为Gabor小波方法。Gabor滤波方法是把不同尺度的纹理特征视为窄带信号，利用具有不同中心频率和带宽的滤波器组来提取这些窄带信号的特征。因此，使用Gabor滤波方法时，首先要设计一组Gabor滤波器，其次利用这个滤波器组对图像进行滤波，从而提取纹理图像在不同频率和方向上的特征。Gabor滤波器组是非正交的，这导致所提取的特征存在大量冗余信息，因此Manjunath和Ma[82]提出了一种有效的Gabor滤波器组设计方案，既能充分提取不同尺度和方向上的纹理特征，又能有效降低所提取特征的冗余度。和小波变换方法相比，Gabor滤波方法具有自己独特的优点：①Gabor滤波方法具有时域和频域的联合最佳分辨率，能达到时频测不准的下界[83]；②Gabor滤波器与哺乳动物视觉皮层上简单细胞的二维感受野的轮廓非常相似，能较好地模拟人类视觉系统的视觉感受特性[84， 85]；③Gabor滤波方法能对图像分解的频率和方向进行任意调节，具有更加灵活的尺度和方向选择性，克服了小波变换在方向选择上的限制。与此同时，现有的Gabor滤波方法也存在一些不足之处：①大部分Gabor滤波方法仅利用滤波后图像幅值的均值和标准差来描述纹理图像的特征[80-82]，这种描述过于粗略，导致基于Gabor滤波的纹理识别方法在识别精度（正确识别的样本个数与全部测试样本个数之比）上不够理想；②Gabor滤波在实现上还没有较好的快速算法，使此类算法的实时性仍有待提高。

进入21世纪，最受瞩目的纹理图像特征提取方法是局部二值模式（Local Binary Pattern， LBP）及其改进算法，它已成为目前最流行的纹理图像特征提取和识别方法。2002年，Ojala等[47]提出了LBP算法，该算法提取的纹理特征不但能获得较高的纹理识别精度，而且具有理论简单、实现高效和对单调的光照变化具有不变性等优点，这使LBP算法成为最受欢迎的纹理特征提取和识别算法。LBP算法的主要思路是对图像的局部邻域特征进行编码，然后计算这些编码值的直方图，将其作为纹理图像的特征描述子。LBP算法的定义公式为

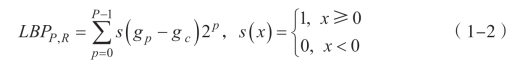
式中：

R —— 局部环形邻域的半径；

P —— 等间隔分布在半径为R的圆上的邻域点个数；

gc —— 局部邻域中心点的灰度值；

gp —— 局部邻域点的灰度值。

可以看出，LBP算法将每个邻域点的灰度值和中心点的灰度值进行比较，如果邻域点的灰度值大于或等于中心点的灰度值，则邻域点被标记为1，否则被标记为0，这样就获得了一个P位的二值编码串，然后将该二值编码串转换为十进制数，作为中心点的LBP编码值。图1-8展示了对图像中一个3×3局部邻域进行LBP编码的过程，中心像素点获得的十进制LBP编码值为76。

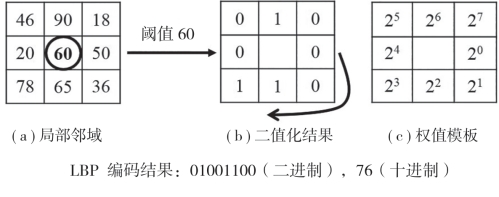
图1-8　LBP算法的编码原理

按照上述方法，对图像中的每个局部邻域进行LBP编码，使每个像素点都获得一个十进制的LBP编码值，从而获得一个LBP编码图像，最后对LBP编码图像计算直方图，并将该直方图作为纹理图像的特征描述子。图1-9展示了利用LBP算法提取纹理图像特征的过程，最终生成的LBP编码图像直方图即可用于纹理图像识别。

图1-9　利用LBP算法提取纹理图像特征的原理

在使用LBP算法时，通过调节环形邻域的半径R和邻域点个数P，可以检测不同尺寸的局部邻域特征，即设置大的（R， P）值可检测大尺寸的邻域特征，设置小的（R， P）值可检测小尺寸的邻域特征。如果将多个半径的特征相结合，则可以同时捕获不同尺寸的LBP特征，实现多尺寸特征融合的目的，进一步提高LBP算法的鉴别能力。图1-10分别展示了（R， P）=（1，8）、（2，16）、（3，24）时的环形邻域结构，如果邻域点没有落在网格的整数坐标处，则可利用插值的方法（如最近邻插值、双线性插值、双立方插值）获得该位置处的灰度值。

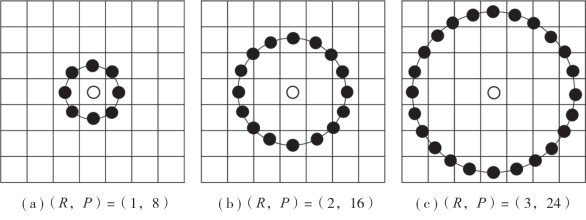
图1-10　LBP算法中三种不同尺寸的环形邻域（R，P）=（1，8）、（2，16）、（3，24）

传统LBP算法虽然具有较好的性能，但也存在如下的不足之处：①不具有旋转不变性。这是因为传统LBP算法采用固定的权值模板，当图像发生旋转时，其对应的二值编码串也随之发生旋转，但权值模板的位置保持不变，从而导致加权求和生成的十进制LBP编码值在旋转前后不一致。因此，相同的纹理特征在旋转前后却对应不同的LBP编码值，即被当成不同的特征对待，从而造成错误的识别结果。②编码的维数太高。例如，当（R， P）=（2， 16）、（3， 24）时，最后生成的直方图维数分别为216和224，特征维数太高，给后续的特征处理和识别带来很大的计算负担，同时需要占用更大的存储空间。③对噪声敏感。当邻域像素和中心像素的灰度值比较接近时，只要其中一个像素的灰度值发生轻微波动，就可能导致LBP编码值发生显著变化，这使非常相似的纹理模式可能会对应显著不同的LBP编码值，从而影响特征描述和识别的稳定性。④仅利用了邻域像素与中心像素灰度差分的符号部分，没有利用像素灰度值差分的幅值和中心像素的灰度等级信息，获取的信息量有限，所提取特征的鉴别能力不足。

为了克服传统LBP算法的上述不足之处，Ojala等[47]进一步提出了具有旋转不变性的LBPri算法和LBPriu2算法，其中LBPriu2算法根据二值化编码中“1”的个数进行编码，最终的十进制编码值只有P+1种情况，特征维数大大降低，方便后续的特征匹配和识别。为了提取更加丰富的纹理特征，Guo等[52]提出了完备的LBP（Completed LBP， CLBP）算法，该算法不但利用了传统LBP算法中邻域像素与中心像素灰度差分的符号信息，还利用了灰度差分的幅值信息，以及中心像素的灰度等级信息，能够捕获更多的局部邻域特征，显著提高了LBP算法的特征描述能力和纹理识别精度。随后，Zhao等[86]受CLBP算法的启发，进一步提出了完备的局部二值计数（Completed Local Binary Count， CLBC）算法，该算法同样利用了局部邻域像素与中心像素灰度差分的符号信息、幅值信息和中心像素的灰度等级信息，能获得与CLBP算法接近的纹理识别精度，但与CLBP算法不同的是CLBC算法在计算局部编码值时不再对二值编码串进行加权求和运算，而是直接将二值编码串中“1”的个数作为局部编码值，这一方面显著降低了局部编码的计算量，另一方面也大大降低了最终生成的直方图特征向量的维数，使CLBC算法获得了更高的实时性，所以CLBC算法在对实时性有较高要求的场合具有很大的优势。大部分LBP类算法只在环形方向上计算编码值，为了捕获多种结构上的纹理信息，Liu等[60]提出了一种扩展的LBP（Extended LBP， ELBP）算法，该算法能够同时在径向方向和环形方向上提取邻域像素与中心像素的灰度差分信息，进一步提高了算法的特征描述能力。随后，Liu等[61]又把中值滤波的方法引入ELBP算法，提出了中值稳健的LBP（Median Robust ELBP，MRELBP）算法，该算法显著提高了LBP算法的抗噪声能力。大部分LBP改进算法在计算最终的LBP图像直方图时，把每个像素的LBP模式值同等看待，即计算直方图时每个像素LBP模式值的加权值都是1，而Guo等[53]提出了一种LBPV算法，该算法同时计算每个像素的LBP模式值和局部方差，在计算LBP图像直方图时将局部方差作为当前像素LBP模式值的加权值，进一步提高了传统LBP算法的特征描述能力。另外，disCLBP算法[49]、DLBP算法[87]和SSLBP算法[55]通过提取纹理图像中占主要部分的主导模式信息，既提升了传统LBP算法的鉴别能力，又降低了特征维数，从而获得了更好的识别性能。目前，LBP及其改进算法以其良好的特征描述能力和实时性，已经在纹理图像特征提取和识别领域获得了最广泛、最深入的研究和应用。

与此同时，考虑到纹理图像是由一些基本的局部单元，即纹理基元（Texton）组成的，并受计算机视觉领域中“视觉词袋（Bag of Visual Words，BoVW）”模型的影响，一些学者提出了基于纹理基元学习的纹理特征提取和识别方法。在这个研究方向上，比较著名的方法有以下三种：①Varma和Zisserman提出了VZ-MR8算法[45]，该算法首先构造一组具有不同尺度和方向的杆状和边缘滤波器，利用这组滤波器对纹理图像进行滤波，并在每个尺度上取最大响应，最终获得8个最大响应（Maximum Response 8， MR8）图像。对于纹理图像的每个像素，其在8个最大响应图像中都有一个对应值，这8个值组成了一个8维的特征向量，用其描述该像素所在的局部邻域特征。其次，利用K-均值算法对所有像素的8维特征向量进行聚类，用最后的聚类结果（即K个8维的特征向量）作为原子构造纹理基元字典。最后，用这个纹理基元字典对训练样本和测试样本的MR8图像进行编码，并计算编码图像的直方图，作为原始纹理图像的特征描述子。②随后，Varma和Zisserman又提出了VZ-Joint算法[46]，该算法不再使用滤波器组进行滤波，而是直接以图像中每个图像块的灰度值作为研究对象，同样利用K-均值算法学习纹理基元字典中的原子聚类算法，后续操作与VZ-MR8算法相同。和VZ-MR8算法相比，VZ-Joint算法省去了滤波器组的设计和滤波过程，纹理识别精度也稍有提高。③最近，Xie等[88]提出了一种有效的纹理基元学习和编码方法，该方法利用L2范数正则化的最小二乘方法来学习纹理基元字典，在对纹理图像进行编码时，不再使用一维的纹理基元序号作为编码值，而是用一个p维的向量来对每个像素进行标记，最后利用纹理基元编码生成的统计特征（Texton Encoding Induced Statistical Features， TEISF）作为纹理图像的特征描述子，从而获得了更高的纹理识别精度。

可以看出，LBP类算法和纹理基元学习类算法在本质上有相似之处，它们都是对局部邻域的特征进行编码，而这个局部邻域就是潜在的纹理基元，所以这两类方法都是在尝试对纹理图像中的纹理基元进行描述和统计。另外，这两类方法也有不同之处，LBP类算法中的编码模式是固定的，每个模式对应一种纹理基元，相当于纹理基元字典已经被预先定义好，不需要字典的学习过程，这大大降低了LBP类算法的计算量，使LBP类算法变得非常高效。而纹理基元学习类算法需要通过不断的学习来获得纹理基元字典，并且这个迭代学习的过程非常耗时，学习到的纹理基元字典的完备性和紧致性也对纹理识别精度有较大影响。通常情况下，LBP类算法的纹理识别精度比纹理基元学习类方法略高，并且LBP类算法在速度上远胜过纹理基元学习类方法。所以，在目前阶段，LBP类方法具有更大的优势，但纹理基元学习类方法仍然具有很大的发展潜力，其特征描述能力和算法的实时性有待进一步提高。

近年来，随着纹理图像识别技术的发展，更复杂、更具挑战性的纹理图像识别任务被提上日程，以前所采用的特征提取方法遇到了瓶颈，在这种情况下，具有特征自主学习能力的深度学习方法开始在纹理图像特征提取领域受到关注。深度学习方法是模拟人脑分层提取特征的机制，利用多层的网络结构，通过对大量的训练样本进行学习，能够自动从样本中提取对分类有用的鉴别性特征，能够创建非常复杂的模型并完成极具挑战性的任务。

目前，深度学习方法在纹理图像特征提取和识别领域的应用还是处于起步阶段，最成功的例子是深度卷积神经网络（Convolutional Neural Network， CNN）的应用。深度CNN模型实际是重复利用卷积滤波、非线性变换（如Sigmoid函数、ReLU函数）和池化（如最大池化、平均池化）等操作，从纹理图像中逐层提取从简单到复杂、从底层到高层、从具体到抽象的特征。另外，深度CNN是一种有监督的特征学习方法，能够根据不同的数据库和任务自动调节模型中的参数，从而学习到与具体任务更加匹配的特征表达。基于以上优点，深度CNN方法在纹理图像特征提取和识别领域开始获得关注和初步的应用。例如，Sifre和Mallat[89]提出了ScatNet算法，该算法首先构建了一个深度卷积网络，卷积层采用尺度和方向都可变的小波滤波器组，其次对空间、旋转和尺度变量进行卷积运算，最后利用散射系数获得纹理图像的特征描述子。冀中等[90]首先利用ImageNet图像数据集[91]训练的CaffeNet模型[92]提取纹理图像特征，该模型包含5个卷积层、3个最大池化层和3个全连接层，其次利用主成分分析（Principal Component Analysis，PCA）算法对提取的纹理特征进行降维，最后利用支持向量机（Support Vector Machine， SVM）分类器进行纹理识别。Andrearczyk和Whelan[93]提出了一种纹理卷积神经网络（Texture Convolutional Neural Network， T-CNN）算法，该算法以现有的CaffeNet模型为基础，并采用与AlexNet模型相同的线性校正、归一化和丢弃（Dropout）操作，同时新增加了一个能量层，从而构建了一个T-CNN模型，然后直接利用现有的图像数据库对该网络模型进行训练，并对最后一个卷积层的能量测度进行池化操作，从而实现了纹理图像的特征提取和识别。英国牛津大学的Cimpoi等[94]研究了在ImageNet数据集上训练的三种CNN模型（AlexNet、VGG-M、VGG-VD），并将CNN模型学习到的局部特征与Fisher向量（Fisher Vector， FV）池化方法相结合，获得了较高的识别精度，并且指出深度CNN的网络层数越深，纹理识别的精度越高。Nguyen等[95]提出了ScatNet_CLBP算法，该算法利用三层的散射网络来捕获纹理图像的宏观结构特征，即把三个散射网络层的系数进行累加作为宏观特征，同时利用CLBP算法提取纹理图像的微观特征，最后把提取的宏观和微观特征进行融合，作为纹理图像的识别特征。以上这些方法都是深度学习方法在纹理图像特征提取和识别领域具有重要意义的尝试，有助于对纹理图像特征进行层次化的表达和深度的理解，为人类最终认识和使用纹理图像开辟了一个崭新的研究方向。

深度学习方法虽然能够自动提取纹理图像特征，但它也存在以下的不足之处：①深度学习方法需要利用大规模的带类别标签的训练样本对CNN模型进行训练，只有在充分训练的情况下才能获得良好的识别性能，如果训练样本的个数较少，对模型的训练不充分，则深度学习方法的识别性能不佳。而目前在纹理图像的特征提取和识别领域，还没有一个大规模的专用纹理图像数据库，无法对深度学习模型进行充分的训练，这也是限制深度学习方法在纹理图像特征提取和识别领域获得广泛研究和应用的主要原因。②深度学习方法非常耗时，CNN模型的结构越复杂、层数越深，需要的训练时间越长。③深度学习方法对硬件平台的计算能力和存储容量都有很高的要求，而高性能的硬件平台通常价格昂贵，这也限制了深度学习方法在纹理图像特征提取和识别领域的广泛应用。基于上述原因，深度学习方法在纹理图像特征提取和识别领域的应用还处于起步阶段，并且发展缓慢，还有很多瓶颈问题有待进一步研究和解决。但与此同时，深度学习方法也带来了新的希望，使以前长期存在的、极具挑战性的纹理特征提取和识别问题有望得到解决。

综上所述，经过50多年的发展，人们在纹理图像的特征提取和识别领域已经取得了丰硕的成果，提出了很多纹理图像特征提取方法，这些方法都具有自己独特的优势和不足之处。同时，因为没有统一的纹理定义和数学模型，人们很难找到一种对所有纹理图像都是最优的特征提取和识别方法，这也是目前多种纹理图像特征提取和识别方法共存并在不同场合发挥作用的原因之一。