主要尺寸包括零件的规格尺寸、有配合要求的尺寸、确定其他零件之间相对位置的尺寸、连接尺寸、安装尺寸等。沿轴线方向上的尺寸A1、A2、A3和间隙尺寸ΔA首尾连接，构成一个环状，反映了主动齿轮轴、泵体、垫片、泵盖各零件沿轴向的尺寸联系。这种确定部件中各零件间相对位置的成组尺寸，称为装配尺寸链。图8-33齿轮泵装配尺寸链3.尺寸基准及其选择度量尺寸的起点，称为尺寸基准，即用来确定其他几何元素位置的一组线、面。......
2023-06-28
如何建立装配尺寸链：极值法和概率法
【摘要】：装配尺寸链的封闭环就是装配后的精度或技术要求。在建立装配尺寸链时，首先应明确封闭环，即将装配精度要求定为封闭环；然后通过对装配关系的分析，即可查明其相应的装配尺寸链的组成环。因此，应分别建立产品部件装配的尺寸链和总装的尺寸链。不论哪种装配尺寸链，其解算的基本方法均有两种：极值法和概率法。
1.装配尺寸链的基本概念
由于装配精度与有关零件的精度有着密切的关系。为了定量地分析这种关系，将尺寸链的基本理论用于装配过程，即建立装配尺寸链进行分析。装配尺寸链就是指由相关零件的有关尺寸（如表面或轴线间的距离）或相互位置关系（如同轴度、平行度、垂直度等）所组成的尺寸链。装配尺寸链的封闭环就是装配后的精度或技术要求。因为这种要求是通过把零部件装配好后才最终形成或保证的，是一个结果尺寸或位置关系。在装配关系中，对装配精度要求有直接影响的那些零部件的有关尺寸或位置关系，就是装配尺寸链的组成环。
2.装配尺寸链的建立
正确建立装配尺寸链是进行尺寸链分析计算的基础。在建立装配尺寸链时，首先应明确封闭环，即将装配精度要求定为封闭环；然后通过对装配关系的分析，即可查明其相应的装配尺寸链的组成环。
装配尺寸链的一般查找方法是：首先将装配精度要求确定为封闭环，然后再取封闭环两端的那两个零件或部件为起点，沿着装配精度要求的方向，以装配基准面的联系为线索，分别查找装配关系中影响装配精度要求的有关零件，直至找到同一个基准零件或同一基准表面为止。这样，所有有关零件上直接连接相邻零部件装配基准面间的尺寸或位置关系，即为装配尺寸链的组成环。
例如，如图8-3所示的装配关系，主轴与尾座的轴心线对溜板移动的等高性要求（AΣ）为封闭环，通过对装配关系的分析，即可查出组成环A1、A2、A3。
图8-3 车床等高性装配尺寸链
e1—滚子轴承外环内滚道对外圆的同轴度；e2—顶尖套锥孔对外圆的同轴度；e3—顶尖套与尾座孔的配合间隙所引起的偏移量
在建立装配尺寸链时，应注意以下几方面：
（1）按一定层次分别建立产品或部件的装配尺寸链。机械产品通常都比较复杂，为了便于装配和提高装配生产率，一般将整个产品划分为若干个部件，装配工作分为部装和总装。因此，应分别建立产品部件装配的尺寸链和总装的尺寸链。这样分层次建立的装配尺寸链比较清晰，表达的装配关系也更加清楚。
（2）在保证装配精度要求的前提下，装配尺寸链可以适当简化。例如，在保证装配精度要求的前提下，图8-3所示的装配尺寸链可简化为8-2 （b）所示的装配尺寸链。
（3）建立装配尺寸链时应遵循“尺寸链最短”（环数最少）原则。由尺寸链的基本理论可知，封闭环公差等于各组成环公差之和。在装配精度一定的条件下，组成环数越少，分配到各组成环的公差就越大，则组成环零件的精度就越容易保证。因此，在建立装配尺寸链时要求组成环的环数应尽可能少一些。如图8-4所示，在图8-2（c）所示的尺寸链中，与封闭环AΣ直接有关的凸台高度AΣ由尺寸B1、B2间接获得，这是不合理的。
（4）当同一装配结构在不同方向上有装配精度要求时，应按不同方向分别建立装配尺寸链。例如，在蜗杆蜗轮副结构中，为了保证蜗杆蜗轮的正常啮合，蜗杆蜗轮副两轴线间的距离、垂直度以及蜗杆轴心线与蜗轮中心平面的重合度均有一定的精度要求。这是三个不同方向的装配精度，因此需要在三个不同方向上分别建立装配尺寸链。
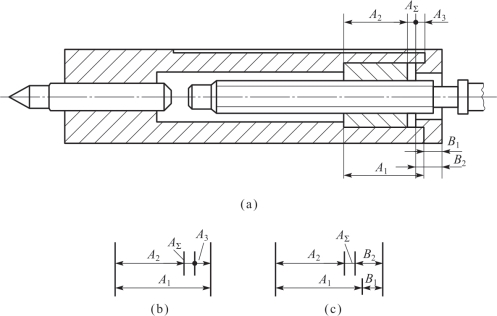
图8-4 车床尾座顶尖套装配图
3.装配尺寸链的计算
装配尺寸链建立后，就需要通过尺寸链的计算来确定封闭环和各组成环之间的数量关系。不论哪种装配尺寸链，其解算的基本方法均有两种：极值法和概率法。极值法是各组成环误差处于对封闭环极不利的情况下，来确定封闭环与组成环关系的一种计算方法。此法的特点是简单可靠，但在封闭环公差较小而组成环的环数又较多时，各组成环的公差太小，使加工困难，增加制造成本，其计算方法详见第4章。概率法是利用概率论原理进行尺寸链计算的一种方法，在上述情况下用概率法比用极值法更合理。下面即着重予以讨论。
（1）各环公差值的概率法计算。在装配尺寸链中，各组成环是有关零件上的加工尺寸或位置关系。这些加工数值是一些彼此独立的随机变量，根据概率论原理，各组成环合成量的封闭环也是一个随机变量，而且两者的标准差σi和σΣ 有下列关系
当加工误差呈正态分布时，其误差量（尺寸分散范围）ω 与标准差间的关系为
ω=6σ
此时，当尺寸链各环均呈正态分布时各组成环的尺寸分散范围为ωi=6σi，封闭环的尺寸范围ωΣ=6σΣ，经变换并代入式（8.1），可得
在各环的误差量ωi 及ωΣ 等于其公差Ti 及TΣ 的条件下，式（8.2）可转化为
上式表明：当各组成环呈正态分布时，封闭环公差等于各组成环公差平方和的平方根。
若各组成环的公差都相等，即Ti=T M，则各组成环的平均公差TM为
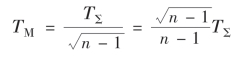
将上式和极值法的TM=
相比，可明显看出，概率法可将组成环的平均公差扩大
倍。n 值越大，TM 越大。由此可见，概率法更适用于环数较多的尺寸链。
应当指出，用概率法解算尺寸链时，封闭环公差TΣ 的取值范围，在正态分布下为6σΣ，对应此范围的概率为0.997 3。这就意味着产品装配后的合格品率并非100%，而不合格品率仅为0.27%，实际上常常忽略不计。
（2）封闭环上下偏差的确定。当各环公差确定后，如能确定各环平均尺寸AM 和平均偏差BMAi，则各环的极限尺寸和偏差就可以方便地计算出来。如图8-5所示，当组成环尺寸分布中心与公差带中心重合时，各组成环的平均尺寸为
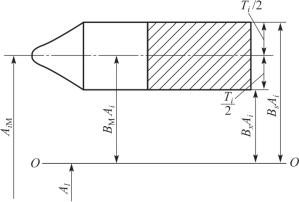
图8-5 正态分布时尺寸的计算关系
由概率论原理可知，封闭环的算术平均尺寸
将式（8.4）代入式（8.5），并化简后得
在求得BMAΣ 及TΣ 之后，可按下式计算封闭环的上下偏差。
上偏差
下偏差
例1 有如图8-4所示的装配尺寸链，图中A1=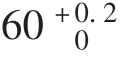
mm，A2=
mm，A3=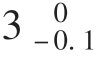
mm，各组成环均呈正态分布，即分布中心与公差带中心重合，求封闭环的尺寸公差。
解：①封闭环的基本尺寸
②封闭环的公差
③封闭环的平均偏差
④封闭环的上下偏差
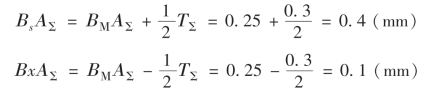
⑤封闭式环尺寸
例2 双联转子泵的轴向装配关系如图8-6所示，要求的轴向间隙为0.05～0.15 mm，A1=41 mm，A3=7 mm，A2=A4=17 mm，求各组成环的公差及偏差。
解：①分析和建立尺寸链
根据双联转子泵的轴向装配关系及题意分析可得其装配尺寸链如图8-7所示。封闭环的尺寸为AΣ=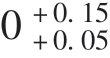
mm，TΣ=0.15-0.05=0.1 （mm）。
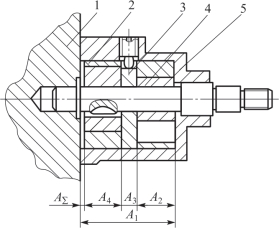
图8-6 双联转子泵的轴向装配关系简图
1—机体；2—外转子；3—隔板；4—内转子；5—壳体
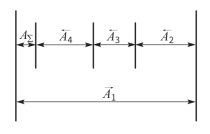
图8-7 轴向装配尺寸链简图
验算封闭环尺寸
②确定各组成环的公差
由于TM=
mm=0.025 mm，隔板尺寸A3 在平面磨床上磨削，容易达到较高的加工精度，其公差可以小些。根据加工的难易程度调整各组成环的公差为T1=0.049 mm，T2=T4=0.18 mm，则
T3=TΣ-(T1+T2+T4)=0.1-(0.049+0.018+0.018)=0.015 (mm)
由此可知：各组成环的加工难易程度大致相同，各组成环的公差较合理。
③计算尺寸A3的偏差。
根据“入体原则”确定有关组成环的偏差为A2=A4=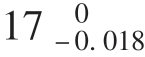
mm，A1=
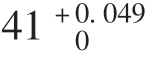mm，根据尺寸链的原理可计算出尺寸A3的偏差。
即
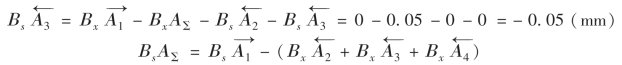
即
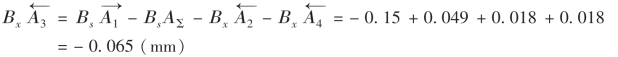
所以隔板尺寸为
有关机械制造技术（第2版）的文章
- 详细阅读
-
前轮01装配体的建立和优化设计详细阅读
图10.9.1 零件模型及模型树Step1.在装配体中创建前轮01。图10.9.2 拉伸1图10.9.3 截面草图Step4.创建图10.9.4所示的实体旋转特征──旋转1。图10.9.7 倒圆角2Step7.创建图10.9.8b所示的抽壳特征──壳1。选择下拉菜单命令；在绘图区选取图10.9.8a所示的面为移除面，输入厚度值3.0。选择下拉菜单命令；选取图10.9.10所示的平面为草绘平面，选取ASM_TOP基准平面为参照平面，方向为；绘制图10.9.11所示的截面草图；选取深度类型为。图10.9.14 倒圆角3Step11.创建图10.9.15所示的拉伸特征──拉伸3。......
2023-06-26
-
如何判断零件尺寸合格？掌握这些尺寸要素和极限详细阅读
由一定大小的线性尺寸或角度尺寸确定的几何形状称为尺寸的要素。尺寸要素允许的尺寸两个极端称为极限尺寸。尺寸要素允许的最大尺寸，称为上极限尺寸，孔、轴分别用Dmax和dmax来表示；而尺寸要素允许的最小尺寸，称为下极限尺寸，孔、轴分别用Dmin和dmin来表示。极限尺寸是以公称尺寸为基数加上其尺寸的极限偏差来确定的。图3-2 圆柱销的极限尺寸......
2023-06-26
-
控制装配体总体尺寸及空间分配详细阅读
2.控制装配体的总体尺寸以及为装配体中各元件分配空间尺寸例如，图6.5.1所示的骨架零件中的DTM3、DTM5基准平面可以控制开启机的总体高度尺寸，TOP和DTM2基准平面决定了零件body的设计空间，DTM4和DTM5基准平面决定了子装配的bottle_asm的设计空间。......
2023-06-20
-
如何建立和运行机构的运动分析详细阅读
向机构装置中增加伺服电动机后，便可建立机构的运动分析（定义）并运行。在每个运动定义中，可选择要打开或关闭的伺服电动机并指定其时间周期，以定义机构的运动方式。可以创建多个运动定义，每个定义都使用不同的伺服电动机和锁定不同的图元。图9.5.64 “分析定义”对话框图9.5.65 “电动机”选项卡定义动画时域。在图9.5.64所示的“分析定义”对话框的区域进行下列操作：①输入开始时间：0。在图9.5.64所示的“分析定义”对话框中，单击按钮。......
2023-06-20
-
如何标注阶梯孔尺寸和粗糙度？详细阅读
图6-83 标注阶梯孔的尺寸和粗糙度分相。图6-85 添加前缀标注孔阶梯孔图2.5单层链式U相绕组展开图用同样的方法可以得到另外两相绕组的连接规律。图6-86 编辑阶梯孔符号7.单击“修改”面板中的“分解”按钮，将编辑后的尺寸分解，尺寸数字和孔深符号分离。标注阶梯孔直径和深度的结果如图6-88所示。......
2023-06-24
-
装配图尺寸标注优化技巧详细阅读
图9-6截止阀的装配图图9-7截止阀的轴测图重要的相对位置尺寸在装配时必须保证的尺寸，如图9-6所示的65，可以看成对内的位置尺寸，即手柄对主要孔的轴线的相对位置。......
2023-06-28
-
滚动轴承装配时的倒角极限尺寸要求详细阅读
对公制系列滚动轴承套圈，GB/T 274—2000规定了其装配倒角的尺寸术语、符号、尺寸极限以及轴和外壳孔的圆角半径。表3-56 向心轴承倒角尺寸最大值 （续）（续）（续）表3-57 圆锥滚子轴承的倒角极限尺寸 （续）① 轴和外壳孔的最大圆角半径见本章第7.2节。表3-59 向心轴承公称倒角尺寸和单向最小倒角尺寸的对照表 表3-60 圆锥滚子轴承公称倒角尺寸和端面最小倒角尺寸对照表......
2023-06-26
相关推荐