实际几何参数与理想几何参数的偏离程度称为加工误差。调整法加工时的调整误差，除上述因素外，还与调整方法有关。主轴回转误差会造成加工零件的形位误差及表面波度和粗糙度。导轨导向误差会造成加工表面的形状与位置误差。4)机床主轴、导轨等的位置关系误差，将使加工表面产生形状与位置误差。表5-1 造成各类加工误差的原始误差......
2023-06-28
加工误差的统计分析方法与应用
【摘要】：由各种工艺因素所产生的加工误差可分为两大类，即系统性误差和随机性误差。机床、夹具、刀具等磨损引起的加工误差，在一次调整后的加工中也均无明显的差异，故也属于常值系统性误差。机床、刀具未达到热平衡时热变形过程中所引起的加工误差，是随加工时间而有规律地变化的，故属于变值系统性误差。
1.系统性误差和随机性误差
生产实际中，影响加工精度的工艺因素往往是错综复杂的。由于多种误差同时作用，有的可以互相补充或抵消，有的则互相叠加，不少原始误差又带来一定的随机性，因此，很难用前述单因素的估算方法来分析，这时只能通过对生产现场实际加工出的一批工件进行检查测量，运用数理统计的方法加以处理和分析，从中找出误差的规律，并加以控制和消除。这就是加工误差的统计分析法，它也是全面质量管理的基础。
由各种工艺因素所产生的加工误差可分为两大类，即系统性误差和随机性误差。
（1）系统性误差。在顺次加工一批工件中，误差的大小和方向保持不变，或按一定规律变化。前者称为常值系统性误差，后者称为变值系统性误差。
加工原理误差，机床、刀具、夹具的制造误差，机床的受力变形等引起的加工误差均与加工时间无关，其大小和方向在一次调整中也基本不变，故都属于常值系统性误差。机床、夹具、刀具等磨损引起的加工误差，在一次调整后的加工中也均无明显的差异，故也属于常值系统性误差。
机床、刀具未达到热平衡时热变形过程中所引起的加工误差，是随加工时间而有规律地变化的，故属于变值系统性误差。
（2）随机性误差。在依次加工一批工件时，加工误差的大小或方向成不规则地变化的误差称为随机性误差。如复映误差、工件的残余应力引起变形产生的加工误差都属于随机性误差。随机误差虽然是不规则地变化的，但只要统计的数量足够多，仍可找出一定的变化规律来。
2.加工误差的统计分析法
常用的统计分析方法是分布曲线法。
（1）实际分布图。用调整法加工出来的一批工件，尺寸总是在一定范围内变化的，这种现象称为尺寸分散。尺寸分散范围就是这批工件最大和最小尺寸之差。如果将这批工件的实际尺寸逐一测量出来，并按一定的尺寸间隔分成若干组，然后以组的尺寸间隔宽度（组距）为底，以频数（同一间隔组的零件数）或频率（频数与该批零件总数之比）为高作出若干矩形，即直方图。以每个区间的中点（中心值）为横坐标，以每组频数或频率为纵坐标得到的一些相应的点连成的折线即为分布折线图。当所测零件数量增多，尺寸间隔很小时，此折线便非常接近于一条曲线，这就是实际分布曲线。
图6-19 活塞销孔直径尺寸分布图
1—理论分布位置；2—公差范围中心（27.992 5）；3—分散范围中心（27.997 9）；4—实际分布位置；5—废品区
图6-19所示为一批
mm活塞销孔镗孔后孔径尺寸的直方图和分布折线图，它根据表6-1数据绘制。
①尺寸分散范围（28.004 mm-27.992 mm=0.012 mm），小于公差带宽度（T=0.015 mm），表示本工序能满足加工精度要求。
②部分工件超出公差范围（阴影部分）成为废品，究其原因是尺寸分散中心（27.997 9 mm）与公差带中心（27.992 5 mm）不重合，存在较大的常值系统性误差（Δ常=0.002 7 mm）。如果使尺寸分散中心与公差带中心重合，把镗刀伸出量调短0.002 7 mm 使分布折线左移到理想位置，则可消除常值系统性误差，使全部尺寸都落在公差带内。
表6-1 活塞销孔直径频数统计表
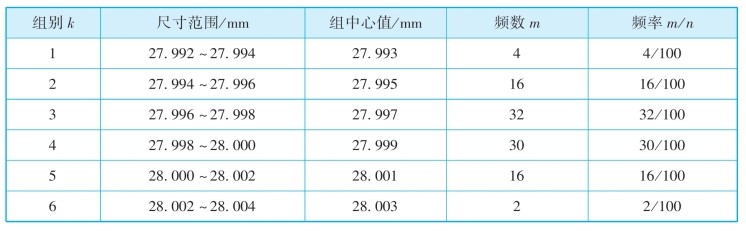
（2）直方图和分布折线图的作法。
①收集数据。通常在同一批次的工作中取100 件（称样本容量），测量各工件的实际尺寸或实际误差，并找出其中的最大值Xmax和最小值Xmin。
②分组。将抽取的工件按尺寸大小分成k 组，通常每组至少有4～5 件。
③计算组距。
组距：
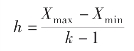
④计算组界。
各组组界：
Xmin ±(j-1)h±h/2
其中，j=1，2，3，4，…，k。
各组的中值：
Xmin+(j-1)h
⑤统计频数mj。
⑥绘制直方图和分布折线图。
（3）正态分布曲线。实践表明，在正常生产条件下，无占优势的影响因素存在，而加工的零件数量又足够多时，各零件尺寸总是按正态分布的。因此在研究加工精度问题时，通常都是用正态分布曲线（高斯曲线）来代替实际分布曲线，使加工误差的分析计算得到简化。
①正态分布曲线方程式
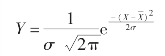
当采用正态分布曲线代替实际分布曲线时，上述方程的各个参数分别为
X——分布曲线的横坐标，表示工件的实际尺寸或实际误差；
——工件的平均尺寸，尺寸的分散中心，即
；
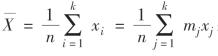σ——均方根偏差，即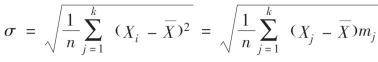
；
Y——分布曲线纵坐标，表示分布曲线概率密度（分布密度）；
n——样本总数；
Xj——组中心值；
k——组数；
e——自然对数底（e=2.718 9）。
正态分布曲线如图6-20所示。曲线下面所包含的全部面积代表了全部工件，即100%。
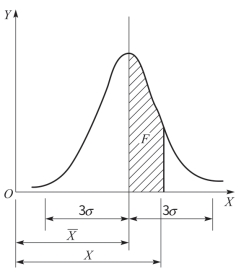
图6-20 正态分布曲线
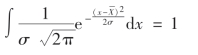
令
则
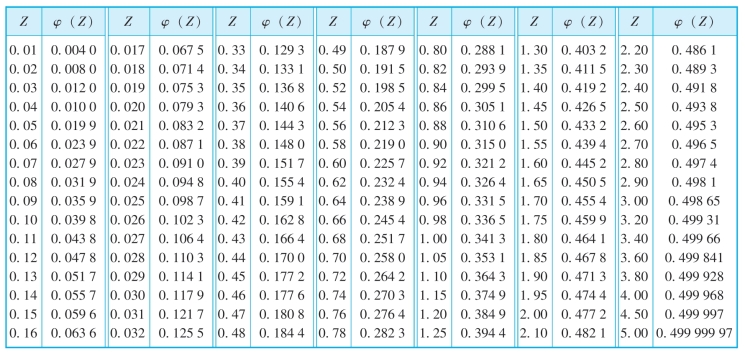
各种不同Z 的函数φ （Z）值见表6-2。
表6-2 φ（Z）=
之值
②正态分布曲线的特点。
a.曲线呈钟形，中间高，两边低。这表示尺寸靠近分散中心的工件占大部分，而尺寸远离分散中心的工件是极少数。
b.曲线以X=
的竖线为轴对称分布，表示工件
尺寸大于
和小于
的频率相等。
c.均方根差σ 是决定曲线形状的重要参数。如图6-21所示，σ 越大，曲线越平坦，尺寸越分散，也就是加工精度越低；σ 越小，曲线越陡峭，尺寸越集中，加工精度越高。
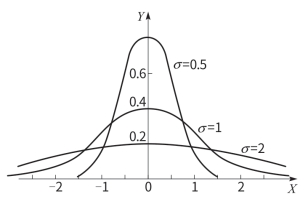
图6-21 正态分布曲线的性质
d.曲线分布中心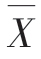
改变时，整个曲线将沿X 轴平移，但曲线的形状保持不变，如图6-22所示。这是常值系统件误差影响的结果。
图6-22 σ 不变时
使分布曲线移动
e.工件尺寸在±3 σ 的频率占99.7%，故一般取6 σ 为正态分布曲线的尺寸分散范围。
例1 已知σ=0.005 mm，零件公差带T=0.02 mm，且公差对称于分散范围中心，X=0.01 mm，试求此时的废品率。
解 Z=X/σ=0.01/0.005=2
查表6-2，当Z=2 时，2φ（Z）=0.954 4，故废品率为
[1-2φ(Z)]×100%=(1-0.954 4)×100%=4.6%
例2 车一批轴的外圆，其图样规定的尺寸为
mm，根据测量结果，此工序的分布曲线是按正态分布，其σ=0.025 mm，曲线的顶峰位置和公差中心相差0.03 mm，偏右端，试求其合格率和废品率。
解 尺寸分布如图6-23所示，合格率由A、B 两部分计算：
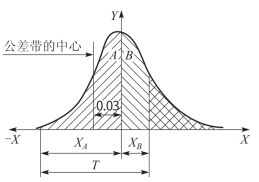
图6-23 轴直径尺寸分布图
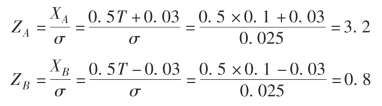
查表得
ZA=3.2 φ(ZA)=0.499 31
ZB=0.8 φ(ZB)=0.288 1
故合格率为
(0.499 31+0.288 1)×100%=78.741%
不合格率为
(0.5-0.288 1)×100%=21.2%
由图6-23可知，虽有废品，但尺寸均大于零件的上限尺寸，故可修复。
③非正态分布。工件实际尺寸的分布情况，有时并不近似于正态分布，而是出现非正态分布。例如将两次调整下加工的零件混在一起，尽管每次调整下加工的零件是按正态分布的，但由于两次调整的工件平均尺寸及工件数可能不同，于是分布曲线将为如图6-24（a）所示的双峰曲线。如果加工中刀具或砂轮的尺寸磨损比较显著，分布曲线就会如图6-24（b）所示形成平顶分布。当工艺系统出现显著的热变形时，分布曲线往往不对称，例如刀具热变形严重，加工轴时曲线偏向左，加工孔时则偏右，如图6-24（c）所示。用试切法加工时，由于操作者主观上存在着宁可返修也不要报废的倾向，也往往出现不对称分布（加工轴宁大勿小，曲线偏右；加工孔宁小勿大，曲线偏左）。
④正态分布曲线的应用。
a.计算合格率和废品率。
b.判断加工误差的性质。如果加工过程中没有变值系统性误差，那么它的尺寸分布应服从正态分布；如果尺寸分散中心与公差带中心重合，则说明不存在常值系统性误差，若不重合则两中心之间存在着距离，即存在常值系统性误差；如果实际尺寸分布与正态分布有较
图6-24 非正态分布曲线
（a）双峰曲线；（b）平顶分布曲线；（c）不对称分布曲线
大出入，说明存在变值系统性误差，则可根据图6-24初步判断变值系统误差是什么类型。
c.判断工序的工艺能力能否满足加工精度的要求。所谓工艺能力是指处于控制状态加工工艺达到产品质量要求的实际能力，可以用工序的尺寸分散范围来表示其工艺能力。大多数加工工艺的分布都接近正态分布，而正态分布的尺寸分散范围是6σ。因此工艺能力能否满足加工精度要求，可以用下式判断：
式中 T——工件公差。
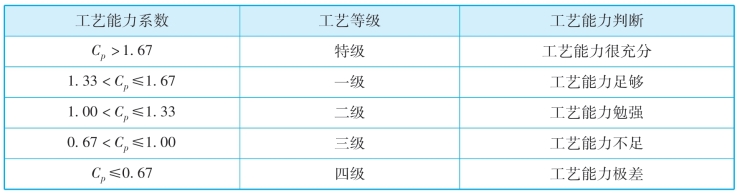
Cp为工艺能力系数。当Cp≥1 时，可认为工序具有不出不合格产品的必要条件；当Cp＜1 时，则该工序产生不合格品是不可避免的。根据工艺能力系数的大小，可将工艺能力分为5 级，见表6-3。
表6-3 工序能力等级表
（4）分布曲线法的缺点。加工中随机性误差和系统性误差同时存在，由于分析时没有考虑到工件加工的先后顺序，故不能反映误差的变化趋势，因此，很难把随机性误差和变值系统性误差区分开来。由于必须要等一批工件加工完毕后才能得出分布情况，因此，不能在加工过程中及时提供控制精度的资料。
有关机械制造技术（第2版）的文章
- 详细阅读
-
应用统计学：估计标准误差详细阅读
估计标准误差也称剩余标准差、回归标准误差，是剩余变差的平均数的平方根。估计标准误差以回归直线为中心，反映各观测值与估计值之间的平均离差程度，用来说明直线回归方程代表性大小的统计分析指标。估计标准误差就是进行这种检测的统计分析指标。估计标准误差的计算方法主要有两个，一个是定义公式，一个是简捷公式。在实践中，在已知直线回归方程的情况下，通常用下面的简捷公式计算估计标准误差。估计标准误差计算如表5-11所示。......
2023-08-13
-
机械基础：产生加工误差的原因详细阅读
工艺系统中的误差是产生零件加工误差的根源，因此把工艺系统中的误差称为原始误差。导轨导向误差直接影响工件的形状及位置精度。但由于在制造及装配过程中会产生误差，所以会引起夹具各元件间的位置误差。定位元件及导向元件与工件及刀具因摩擦而磨损，使加工产生误差。......
2023-06-25
-
齿轮加工误差分类方法详解详细阅读
为了分析齿轮各种误差的性质、规律以及对传动精度的影响，将齿轮的加工误差按不同规律分类。齿轮加工过程中，几何偏心和运动偏心所产生的误差均属于长周期误差。图7-5齿轮的周期性偏差2.按齿轮误差的方向分按齿轮误差的方向分为径向误差、切向误差、轴向误差和展成面误差。展成面误差是指切齿刀具展成面的误差。......
2023-06-15
-
应用多元统计分析方法：基于R实验详细阅读
多元统计分析是统计学中应用性很强的一个分支，它的应用范围十分广泛．多元统计分析可以应用于几乎所有的领域，主要包括经济学、农业、地质学、医学、工业、气象学、金融、精算、物理学、地理学、军事科学、文学、法律、环境科学、考古学、体育科学、遗传学、教育学、生物学、管理科学、水文学等，还有一些交叉学科或方向等．多元统计分析的应用实在是难以一一罗列，以下简要地介绍一下多元统计分析在文学、数据挖掘（作为交叉学科......
2023-11-18
- 详细阅读
-
机械加工技术的经济分析方法详细阅读
制定机械加工工艺规程时，在能满足工件的各项技术要求下，一般可以拟订出几种不同的加工方案，而这些方案的生产效率和生产成本会有所不同。为了选取最佳方案就需进行技术经济分析。产量小于这个范围时，由于S/N 比值增大，工艺成本就增加。当产量超过这个范围时，由于S/N 比值变小，这时就需要投资更大而生产率更高的设备，以便减少V 而获得更好的经济效益。......
2023-06-29
-
物相衍射分析方法与应用详细阅读
对于混合物来说，各个晶相的衍射花样会同时出现，而不会出现干涉。X射线物相分析可以鉴别样品中的物相，包括纯元素（单质）、化合物和固溶体。同一种材料，可以具有不同的物相，称为同分异构体。就广义而言，物相衍射分析包括物相鉴定、定量分析、相结构的测定以及相变过程检测等。但对于纳米材料，晶粒的小尺寸会导致衍射峰的宽化，进而影响积分强度的计算，所以纳米材料定量分析的精度和准确度都远低于传统材料。......
2023-06-20
相关推荐