如何评价测量方法的精密度？

2023-06-29 理论教育版权反馈

【摘要】：精密度是在规定条件下独立测试结果间的一致程度。重复性条件和再现性条件是精密度定义所指“规定条件”的两个极端条件，这两个条件对很多实际情况是必需的，对描述测量方法的变异性是有用的。根据精密度规定条件的分类，精密度可分为重复性条件下的精密度、中间条件下的精密度和再现性条件下精密度。目前，作为解释测量结果，评价、选择测试方法的重要依据，采用Sr和SR来表示方法的精密度已为国际先进标准所广泛采用［21，22］。

精密度是在规定条件下独立测试结果间的一致程度。重复性条件和再现性条件是精密度定义所指“规定条件”的两个极端条件，这两个条件对很多实际情况是必需的，对描述测量方法的变异性是有用的。重复性条件（repeatability conditions）指在同一实验室，由同一操作员使用相同的设备，按相同的测试方法，在短时间内对同一被测对象相互独立进行的测试条件；再现性条件（reproducibility conditions）指在不同的实验室，由不同的操作员使用不同设备，按相同的测试方法，对同一被测对象相互独立进行的测试条件。由此可见，在使用相同测试方法对同一被测对象相互独立进行的测试过程中，影响精密度条件的因素主要包括：操作人员、使用的设备、设备的校准、环境（温度、湿度、空气污染等）、不同测量的时间间隔等^［17］。当上述影响因素的一个或多个允许变化时，位于重复性条件和再现性条件的中间条件也是可以想象的，常称为中间精密度条件。

根据精密度规定条件的分类，精密度可分为重复性条件下的精密度、中间条件下的精密度和再现性条件下精密度。其中，在重复性条件下的精密度称为重复性（repeatability），在再现性条件下的精密度称为再现性（reproduc-ibility）。

在日常检测工作中，精密度（变异性）常简单的采用一组测量数据的标准偏差（S）或相对标准偏差（RSD）表示。当一组检测结果为x₁，…，x_n时，S和RSD的计算按照式（2－14）和式（2－15）获得。

式（2－14）和式（2－15）中，为测量结果算数平均值。

例2－10给出计算一组测量结果算术平均值、标准偏差和相对标准偏差的示例。

【例2－10】计算一组测量结果的平均值、标准偏差和相对标准偏差

在重复性条件下，对烟用接装纸质控样品外层Cr元素进行测定，测定结果分别为2.72，2.58，2.75，2.74，2.67，2.51，2.77，2.80，2.59，2.84mg/kg，计算这一组测量结果的平均值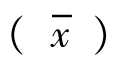、标准偏差（S）和相对标准偏差（RSD）。

注：该实例参见文献［18］中均匀性测试部分。

解：

按照式（2－14）和式（2－15）计算获得这一组测量结果的平均值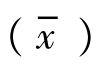、标准偏差（S）和相对标准偏差（RSD），结果如下：

综上，这一组测量结果的平均值为2.70mg/kg、标准偏差为0.11mg/kg，相对标准偏差为4.1%。

《GB/T 6379.2—2004/ISO 5725－2：1994测量方法与结果的准确度（正确度和精密度）第2部分：确定标准测量方法重复性和再现性的基本方法》给出了通过协同实验室间试验获得测量方法精密度的数值估计的基本方法^［19］。该标准规定了通过实验室间协同试验，用数理统计方法，计算并确定标准测量方法的重复性标准差（S_r）和再现性标准差（S_R）数值，并确定S_r和S_R与测量水平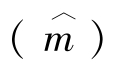的函数关系，简称方法精密度，用测试方法的“精密度”代替传统的“允许差”^［20］。目前，作为解释测量结果，评价、选择测试方法的重要依据，采用S_r和S_R来表示方法的精密度已为国际先进标准所广泛采用^{［21，22］}。

按照GB/T 6379.2—2004/ISO 5725－2：1994标准的方法，当测量水平为m时，S_r和S_R的计算方法如下：

式中 n_i——第i号实验室对m水平样品的测试结果个数；

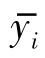——第i号实验室对m水平样品的测定结果算术平均值；

S_i——第i号实验室对m水平样品的测定结果标准偏差；

p——参加实验室间协同试验的实验实数；

S_L——参加实验室间的标准偏差；

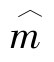——协同试验对m水平样品的测定结果总平均值估计值；水平。

例2－11给出了计算S_r和S_R的简单示例。

【例2－11】根据实验室间协同试验结果，评价烟用纸张中丁酮的精密度

参考文献［23］中烟用纸张中B样品中丁酮溶剂残留标准测量方法的共同实验结果，计算获得烟用纸张中B样品丁酮测量结果精密度。为使本示例避免过去冗繁，仅选取文献［23］中8家（p）经柯克伦最大方差比检验法^［24］和拉布斯检验改进方法^［25］离群值检查合格的实验室检测结果，8家实验室检测结果如表2－8所示。

表2－8 烟用纸张中丁酮的检测结果

解：

按照式（2－16）到式（2－24），获得相关统计量结果如下：

最终，按照GB/T 6379.2—2004/ISO 5725－2：1994标准推荐方法，所获得1.5101mg/m²丁酮含量水平的重复性标准差为0.0460mg/m²，再现性标准差为0.0962mg/m²。

根据式（2－15）还可以进一步计算出相对重复性标准差（RSD_r）和相对再现性标准差（RSD_R），结果如下：

GB/T 6379.2—2004/ISO 5725－2：1994主要研究在重复性条件和再现性条件下测量的各种标准的估计。然而在通常的实验室工作中往往要求对两个（或多个）测试结果观测值的差进行检查，为此需确定一些类似临界差之类的度量，如重复性限（repeatability limit，用符号r表示）和再现性限（repro-ducibility limit，用符号R表示），而不是标准差^［26］。其中，重复性限的定义为一个数值，在重复性条件下，两个测试结果的绝对差小于或等于此数的概率为95%；再现性限的定义为一个数值，在再现性条件下，两个测试结果的绝对差小于或等于此数的概率为95%^［17］。在《GB/T 6379.6—2009/ISO 5725－6：1994测量方法与结果的准确度（正确度和精密度）第6部分：准确度的实际应用》中，该标准给出了计算r和R的计算方法［式（2－25）和式（2－26）］。

当通过协同实验室间试验获得测量方法精密度时，往往需要在精密度试验计划中考虑如何实施有效的协同试验。其中最为常见也是比较突出的问题是：宜征集多少家实验室来协作进行试验？每家实验室宜进行多少次重复测试？

按照GB/T 6379.1—2004/ISO 5725－1：1994^［17］给出的95%置信概率下S_r和S_R估计值的不确定度系数计算方法，获得不同实验室数（p）对应不同测试结果数（n）的S_r的不确定度系数以及S_R的不确定度系数，取再现性标准差与重复性标准差的比值（γ）为2。从结果（图2－13和图2－14）可以直观看出，对于实验室数而言，当参加精密度试验的实验室数目很少时，S_r和S_R的不确定度系数较高；而当p＞20时，再增加2～3个实验室只能使不确定度降低很少，因此，GB/T 6379.1—2004/ISO 5725－1：1994推荐参加精密度试验的实验室数p通常取8～15。对于重复测试次数而言，增加每个实验室测试结果数（n＞2）有利于降低不确定度系数，特别是降低S_r不确定度系数；但当保证了足够的实验室数后，再增加每个实验室测试结果数对不确定的影响不明显。因此，参加精密度试验的每个实验室测试结果数n通常取3～5。

图2－13 以概率水平95%，预期S_r的偏离不超过其真值的倍数

图2－14 以概率水平95%，预期S_R的偏离不超过其真值的倍数（γ＝2）

精密度的结果往往依赖于测量水平，通常在化学分析中，测量水平的浓度值越大，测量结果间的变异性越小，精密度越高；测量水平的浓度越小，测量结果的变异性越大，精密度越低。1980年，Horwitz，Kamps和Boyer对美国分析化学家协会（AOAC）组织的50多个不同测试项目的实验室间协同试验结果进行了核查，结果发现，测量水平的质量浓度与再现性存在一定的函数关系^［27］。而后，在化学分析领域，Horwitz方程被广泛作为测量结果精密度的评价依据。

通常，在工作范围内，精密度研究及评价准则要求如下^［2，28］：

（1）实验室应在标准曲线所确定的工作范围内研究精密度绝对值与目标组分浓度的关系。化学分析中，一般情况下，精密度的绝对值与目标组分浓度或含量呈线性关系，个别情况下，取对数或变化成相对标准偏差后是一个常数。

（2）可将使用Horwitz方程计算的结果用于评价精密度。Horwitz方程为式（2－27）。表2－9是用Horwitz方程计算得到的预测再现性相对标准偏差结果。

（3）在重复性条件下，HorRat比值的结果通常在1/3～1/2。

（4）在再现性条件下，HorRat比值的结果通常不大于1。

注：HorRat比值^［29］的计算按照式（2－28）计算获得。

式中 PRSD_R——预测再现性相对标准偏差；

C——目标分析物的浓度质量分数。

式中RSD为实验室评估获得的实际重复性相对标准偏差或再现性标准偏差。

表2－9 Horwitz方程计算得到的预测PRSD_R

注：ppm（parts per million），指百万分之一，1ppm＝10^－6＝1mg/kg；ppb（parts per billion），指十亿分之一，1ppb＝10^－9＝1μg/kg。