量子遗传算法是一种将遗传算法和量子计算相结合的概率优化方法，两者相互作用。量子遗传算法是一种将量子比特的概率幅用于染色体编码，用量子门的调整操作来实现染色体更新，以完成进化搜索的方法。量子遗传算法的流程如下：初始化种群Q，随机生成n个用量子比特编码的染色体。......
2023-06-29
模拟退火算法优化
【摘要】：模拟退火算法是由N Metropolis等学者于1953年最早提出的。模拟退火算法从某一给定的初始温度开始，随着迭代的进行，温度参数不断下降，结合算法概率性的突跳能力在问题的可行解空间中随机寻找目标函数的解，并以Metropolis准则判定是否接受新解，如此迭代进行下去，逐步寻找问题的全局最优解。Metropolis接受准则是模拟退火算法的重要核心思想，Metropolis接受准则也是依据固体物质退火过程的特点而提出的。图11-2模拟退火算法流程图③算法运算产生新解。
模拟退火算法（simulated annealing，SA）是由N Metropolis等学者于1953年最早提出的。直到1983年，S Kirkpatrick等人将模拟退火的核心思想应用到复杂组合优化问题中并获得良好的应用效果，该算法是一种基于Mente-Carlo迭代求解策略的随机寻优算法，其算法思想来源于物理中的固体降温退火过程与数学中的许多组合优化问题之间的相似性。
模拟退火算法从某一给定的初始温度开始，随着迭代的进行，温度参数不断下降，结合算法概率性的突跳能力在问题的可行解空间中随机寻找目标函数的解，并以Metropolis准则判定是否接受新解，如此迭代进行下去，逐步寻找问题的全局最优解。
Metropolis接受准则是模拟退火算法的重要核心思想，Metropolis接受准则也是依据固体物质退火过程的特点而提出的。物理中固体在退火过程中，主要有三大物理过程。
①升温过程。当固体物质温度升高时，物质内部粒子能量升高，粒子的运动增强。当温度升高到一定程度，内部粒子运动脱离其平衡位置，固体就会熔化成为液体状态。
②等温过程。当物质温度降低到恰好与周围环境相同时，物质将暂时停止向周围环境散发热量。此时，物质温度保持不变，但是物质内部的粒子自由能会逐渐降低，当物质内部粒子的自由能降低到当前物质温度所蕴含的能量能够维持的最低状态时，物质会进入平衡态。物质温度保持不变，但内部粒子自由能减少到达到平衡态的整个过程就是等温过程。
③冷却过程。物质温度降低到一定程度后，物质内部的粒子能量逐渐减少，粒子运动逐渐减弱，直至所有粒子运动渐趋稳定。此时，物质内部系统能量下降到当前环境中的最低值，物质内部粒子将重新进入平衡状态。表现在外就是物质重新凝结成为固态，此时的物质内部能量比熔化前的固体状态更低。
智能优化算法的提出是为了使目标函数值达到最优而设计的，因此，在退火迭代过程中，接受优化解的概率应该大于接受劣化解的概率；并且随着温度的下降，接受优化解的概率增加而接受劣化解的概率减少。当温度趋于0℃，接受劣化解的概率也趋近于0。
模拟退火算法的基本步骤（图11-2）如下。
①初始化。设定初始温度，初始解，每个温度的迭代次数，温度的衰减系数。初始温度的设定对于算法从随机搜索过程转换成局部搜索的速度起到控制性作用；迭代次数的设定对于算法搜索解的质量有显著作用；衰减系数一般设置接近1，衰减系数的设定对于算法的搜索精度与算法运算速度起控制作用。
②对于温度进行其对于迭代次数，迭代步骤③到⑤的操作。
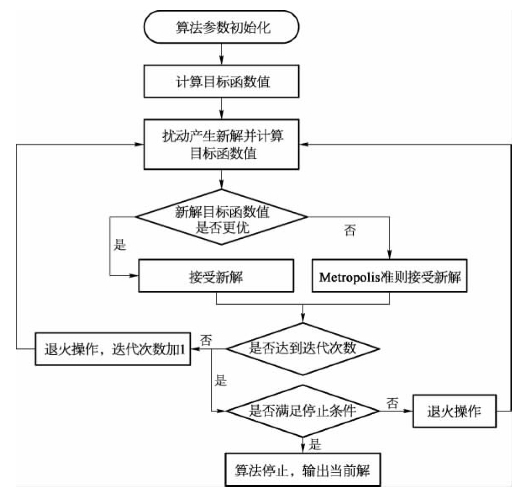
图11-2 模拟退火算法流程图
③算法运算产生新解。
④计算目标函数值的差值。若差值小于0，则接受新解；否则以一定概率接受新解。
⑤对比算法终止条件，满足终止条件则输出当前解为最优解，结束算法；不满足终止条件，继续步骤⑥。
⑥对当前温度值进行衰减系数为初始化系统的衰减计算，然后继续步骤②。
有关工业智能技术与应用的文章
- 详细阅读
-
混沌粒子群优化算法优化方案探究详细阅读
混沌粒子群优化算法的基本思想是采用混沌序列初始化粒子的位置和速度,先对当前粒子群体中的最优粒子进行混沌寻优,然后把混沌寻优的结果随机替换粒子群体中的一个粒子。,z1N),根据式(4-6)得到N个向量z1,z2,…如果粒子适应度优于全局极值gbest,则将gbest设置为新位置。则混沌粒子群优化算法的流程为:初始化,设置最大允许迭代次数或适应误差限,以及CPSO算法的参数惯性权值和学习因子。,PgD)进行混沌优化:将Pgi(i=1,2,…计算其适应值,得到性能最好的可行解pb。......
2023-06-23
-
熔透控制算法优化方案详细阅读
在TIG焊熔透控制系统中，控制器采用的是模糊PID控制方法，这种控制系统在焊接过程中具有自校正控制的功能。熔透控制是在起弧稳定后开始的，为了保证控制的准确性，取前10个周期的熔宽平均值作为整个控制过程的熔宽参考值。根据这些控制规则，再按照模糊控制推理合成规则进行运算，采用最大隶属度方法进行模糊判决，经过多次的试验和修改，得到最终的模糊控制表。......
2023-06-26
-
支持向量机优化算法详细阅读
支持向量机是机器学习中的一项新技术，是借助于最优化方法来解决机器学习问题的新工具，开始成为克服维数灾难和过学习等困难的强有力的手段。支持向量机方法建立在统计学理论的VC维理论和结构风险最小原理基础之上，根据有限样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的推广能力。支持向量机正是这样一种努力最小化结构风险的算法。这个归一化的结果便是支持向量机的几何间隔。......
2023-06-28
-
遗传算法优化问题求解详细阅读
遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。遗传算法之所以具备强大的搜索能力，是因为包罗了选择、杂交和变异三种基本操作算子，同时这三种操作算子也是模拟自然生物圈中自然存在的有性繁殖、杂交和变异等现象的核心载体。同样，遗传算法中起核心作用的是遗传操作的交叉算子。通过交叉，遗传算法的搜索能力得以飞跃提高。图11-1遗传算法流程图......
2023-06-28
-
中文分词算法的优化策略详细阅读
一般来说，中文分词在具体的算法实现上分为三种：基于字符串匹配的分词方法、基于理解的分词方法和基于统计的分词方法。在中文搜索引擎中，目前基本上是这三种算法混合使用。2）基于统计的分词方法基于统计的分词方法也叫最大概率分词方法。作为中文分词基础的词库，新词补充和老词删除就是非常重要的工作。比如“测试”在“每台计算机在出厂前都要经过严格的测试”这句话中是典型的动词，而在“软件测试领域”中是一个名词。......
2023-07-02
-
窃听感知路由及其分配算法优化详细阅读
在这个算法中，RSA问题被分解成两个子问题：路由子问题与频谱分配子问题。ES-RSA算法的伪代码如图8-3所示，当业务到达网络时，首先通过KSP算法找到k条最短路径，然后根据窃听概率分布计算出每条路径被窃听的概率，将路径窃听概率不满足高于业务需求MIRP值的路径删除，在路径选择结束后，利用首次适用算法进行频谱分配，由此得到资源分配结构。通过设置MIRP值条件可以有效地去除泄露概率较高的路径，由此降低被窃听的概率，实现安全性的提升。......
2023-06-19
-
多目标蚁群算法模型优化详细阅读
算法根据决策变量X和式～式的约束条件依次确定任务续传调度标识符和相应的执行时间，从而得到决策变量X的目标函数。图9-27可用时间窗口更新交叉；嵌入；包含；无关确定所有任务的续传调度标识和执行时间后，计算目标函数F=｛f 1，f 2，f 3｝，即可评价此调度方案优劣。......
2023-07-02
相关推荐