图像分析及分类技术简介

2023-06-28 理论教育版权反馈

【摘要】：SVM支持向量机SVM是从线性可分情况下的最优分类面发展而来的，基本思想可用图10-8所示的两维情况说明。满足条件约束条件且使‖w‖/2最小的分类面就叫做最优分类面，H1、H2上的训练样本点称为支持向量。图10-9给出了K近邻分类器的示意图。在性能上最近邻分类器虽然简单，但是泛化错误不超过贝叶斯最优分类器的两倍。

机器视觉必须完成的一个任务是识别。在完成对物体的图像特性采集和提取后，系统必须找到一种方法将其归为一个已知类即赋予该物体一个已知的类别。模式分类领域提供了完成这个任务的算法。

现代网络上图片视频这种计算机图形信息与日俱增，人们期望能对处理后的图像迅速而有准确的归类；因此，与机器学习这一前沿领域结合，为构造大规模的计算机视觉系统提供了可能。

（1）SVM支持向量机

SVM是从线性可分情况下的最优分类面发展而来的，基本思想可用图10-8所示的两维情况说明。图中，实心点和空心点代表两类样本，H为分类线，H1、H2分别为过各类中离分类线最近的样本且平行于分类线的直线，它们之间的距离叫做分类间隔（margin）。所谓最优分类线就是要求分类线不但能将两类正确分开（训练错误率为0），而且使分类间隔最大。分类线方程为wx+b=0，可以对它进行归一化，使得对线性可分的样本集：

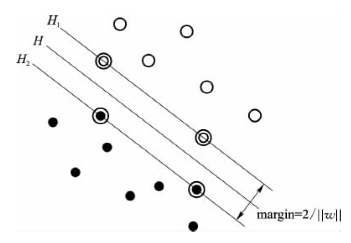
pagenumber_ebook=250,pagenumber_book=234

图10-8　SVM基本思想

（Xi，Yi），i=1，…，n，x∈Rd，y∈｛+1，-1｝

满足约束条件：

Yi［（wXi）+b］-1≥0，i=1，…，n

此时分类间隔等于2/‖w‖，使间隔最大等价于使‖w‖/2最小。满足条件约束条件且使‖w‖/2最小的分类面就叫做最优分类面，H1、H2上的训练样本点称为支持向量。

图10-8最大线性可分，于是可以总结出，想要找到样本空间内最大划分平面可以转化为求解以下数学问题：

minw，b‖w‖2/2

Yi［（wXi）+b］-1≥0

这就是支持向量机的基本型。

模式识别方面最突出的应用研究是贝尔实验室对美国邮政手写数字库进行的实，这是一个可识别性较差的数据库，人工识别平均错误率是2.5%，用决策树方法识别错误率是16.2%，两层神经网络中错误率最小的是5.9%，专门针对该特定问题设计的五层神经网络错误率为5.1%（其中利用了大量先验知识），而用三种SVM方法得到的错误率分别为4.0%、4.1%和4.2%，且其中直接采用了16×16的字符点阵作为SVM的输入，并没有进行专门的特征提取。实验一方面说明了SVM方法较传统方法有明显的优势，同时也得到了不同的SVM方法可以得到性能相近的结果（不像神经网络那样依赖于模型的选择）。

（2）K-NN算法

K近邻学习是一种常见的监督学习方法，其工作机制非常简单：给定测试样本，基于某种距离度量找出与其最靠近的k个最靠近的样本，然后基于这k个邻居的信息来进行预测。通常，在分类任务中可使用投票法，即基于这k个样本中出现最多的类别来作为预测的结果。在回归任务使用平均法，即将这k个样本的输出平均值来作为预测的结果。

与一般的机器学习方法，K近邻算法有一个显著的不同之处。它没有显式的训练过程，是懒惰学习的代表，此类算法仅仅是将样本保存起来，训练开销为零，待收到测试样本再进行处理。

图10-9给出了K近邻分类器的示意图。显然，k是一个重要参数，当k取不同值时，分类器会输出不同结果。另一方面，若是选取不同的距离计算方式，输出的结果也会显著不同。

图10-9中，当k=3时，圆形点被判定为三角形，因为与它最近的3个邻居中有2个是三角形按照投票法，圆形点被预测为三角形；当k=5时，圆形点被算作正方形，与它最近的5个邻居中有3个是正方形。

在性能上最近邻分类器虽然简单，但是泛化错误不超过贝叶斯最优分类器的两倍。

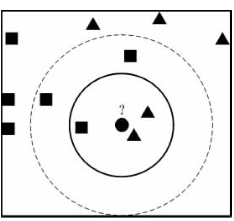
pagenumber_ebook=251,pagenumber_book=235

图10-9　k邻近算法的示意图

图像分析及分类技术简介

相关推荐