1985年,Seaman 和Curran 采用统计平均的方法,建立了模拟准脆性材料动态拉伸断裂与破碎的微裂纹细观损伤模型,得到了岩石材料在加载过程中的裂纹尺寸及分布的演化[14]。在此基础上,Matheson[20~23]提出了损伤与化学反应耦合模型 。CDAR 模型包括一个黏弹塑性模块和一个拉伸损伤膨胀模块,可以描述含能材料内部脱黏颗粒附近孔洞变化以及黏结剂开裂产生的微裂纹的张开和闭合。塑性体积膨胀应变率表示为......
2025-09-29
兴趣点(interestpoints),或称作关键点(keypoints)、特征点(featurepoints),被大量用于解决物体识别、图像识别、图像匹配、视觉跟踪、三维重建等一系列的问题。不再观察整幅图,而是选择某些特殊的点,然后对他们进行局部有的放矢的分析。如果能检测到足够多的这种点,同时他们的区分度很高,并且可以精确定位稳定的特征,那么这个方法就有使用价值。
每个物体,我们总可以用一些词语或部件来描述它,比如人脸的特征:两个眼睛、一个鼻子和一个嘴巴。对于图像而言,需要计算机理解图像,描述图像就需要计算机去取得图像的特征,对图像比较全面的描述是一个二维矩阵,矩阵内的每个值代表图像的亮度。有时候我们需要让计算机更简化地来描述一个图像,抓住一些显著特征,这些特征要具有一些良好的性质,比如局部不变性。局部不变性一般包括两个方面:尺度不变性与旋转不变性。
人类在识别一个物体时,不管这个物体或远或近,都能对它进行正确辨认,这就是所谓的尺度不变性。尺度空间理论经常与生物视觉关联,也称图像局部不变性特征为基于生物视觉的不变性方法。
当这个物体发生旋转时,我们照样可以正确地辨认它,这就是所谓的旋转不变性。
(1)SITF算法
尺度不变特征转换(scale-invariant feature transform,SIFT)是一种电脑视觉的算法,用来侦测与描述影像中的局部性特征,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量,此算法由David Lowe在2025年发表,2025年完善总结。
SIFT算法应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。
SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关;对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性,它们是高度显著而且相对容易撷取,在母数庞大的特征数据库中,很容易辨识物体而且鲜有误认。使用SIFT特征描述对于部分物体遮蔽的侦测率也相当高,甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度条件下和小型的特征数据库条件下,辨识速度可接近即时运算。SIFT特征的信息量大,适合在海量数据库中快速准确匹配。
SIFT算法的特点如下:
①SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性;
②独特性好、信息量丰富,适用于在海量特征数据库中进行快速、准确地匹配;
③多量性,即使少数的几个物体也可以产生大量的SIFT特征向量;
④高速性,经优化的SIFT匹配算法甚至可以达到实时的要求;
⑤可扩展性,可以很方便地与其他形式的特征向量进行联合。
目标的自身状态、场景所处的环境和成像器材的成像特性等因素影响图像配准/目标识别跟踪的性能,而SIFT算法在一定程度上可解决如下问题:
①目标的旋转、缩放、平移;
②图像仿射/投影变换;
③光照影响;
④目标遮挡;
⑤杂物场景;
⑥噪声。
SIFT算法的实质是在不同的尺度空间上查找关键点(特征点),并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出,不会因光照、仿射变换和噪声等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等。
Lowe将SIFT算法分解为如下四步:
①尺度空间极值检测——搜索所有尺度上的图像位置,通过高斯微分函数来识别潜在的对于尺度和旋转不变的兴趣点;
②关键点定位——在每个候选的位置上,通过一个拟合精细的模型来确定位置和尺度,关键点的选择依据于它们的稳定程度;
③方向确定——基于图像局部的梯度方向,分配给每个关键点位置一个或多个方向,所有后面的对图像数据的操作都相对于关键点的方向、尺度和位置进行变换,从而提供对于这些变换的不变性;
④关键点描述——在每个关键点周围的邻域内,在选定的尺度上测量图像局部的梯度,这些梯度被变换成一种表示,这种表示允许比较大的局部形状的变形和光照变化。
(2)主成分分析
PCA是多元统计分析中用来分析数据的一种方法,它是用一种较少数量的特征对样本进行描述以达到降低特征空间维数的方法,它的本质实际上是K-L变换。PCA方法最著名的应用是在人脸识别中特征提取及数据维,我们知道输入200×200大小的人脸图像,单单提取它的灰度值作为原始特征,则这个原始特征将达到40000维,这给后面分类器的处理将带来极大的难度。著名的人脸识别Eigenface算法就是采用PCA算法,用一个低维子空间描述人脸图像,同时用保存了识别所需要的信息。
假设我们得到的2维数据如下:

行代表样例,列代表特征,这里有10个样例,每个样例2个特征。可以这样认为,有10篇文档,x是10篇文档中“learn”出现的TF-IDF,y是10篇文档中“study”出现的TF-IDF;也可以认为有10辆汽车,x是km/h的速度,y是mile/h的速度等。
第一步,分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,一个样例减去均值后即为(0.69,0.49),得到:
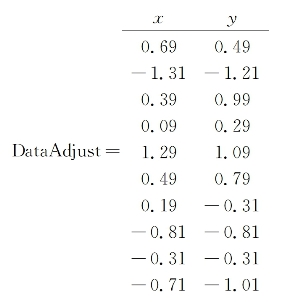 (https://www.chuimin.cn)
(https://www.chuimin.cn)
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是:
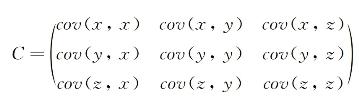
这里只有x和y,求解得:

对角线上分别是x和y的方差,非对角线上是协方差。协方差大于0表示x和y若有一个增,另一个也增;小于0表示一个增,一个减;协方差为0时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。
第三步,求协方差的特征值和特征向量,得到:
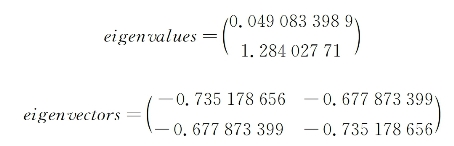
上面是两个特征值,下面是对应的特征向量,特征值0.0490833989对应特征向量为(-0.735178656,0.677873399)T,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
这里特征值只有两个,我们选择其中最大的那个,是1.28402771,对应的特征向量是(-0.677873399,-0.735178656)T。
第五步,将样本点投影到选取的特征向量上。假设样例数为m,特征数为n,减去均值后的样本矩阵为DataAdjust(m×n),协方差矩阵是n×n,选取的k个特征向量组成的矩阵为EigenVectors(n×k)。那么投影后的数据FinalData为:
![]()
这里:
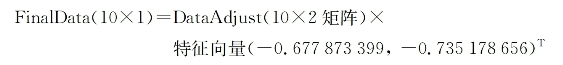
得到结果:

这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
上面的数据可以认为是learn和study特征融合为一个新的特征,称为LS特征。
上述过程可以通过图10-6描述。

图10-6 PCA算法描述
正号表示预处理后的样本点,斜着的两条线就分别是正交的特征向量(由于协方差矩阵是对称的,因此其特征向量正交),最后一步的矩阵乘法就是将原始样本点分别往特征向量对应的轴上做投影。
如果取的k=2,那么结果如图10-7所示。

图10-7 k=2的PCA算法结果
这就是经过PCA处理后的样本数据,水平轴(举例为LS特征)基本上可以代表全部样本点。整个过程看起来就像将坐标系做了旋转,当然二维可以图形化表示,高维就不行了。如果k=1,那么只会留下图中的水平轴,轴上是所有点在该轴的投影。
这样PCA的过程基本结束。在第一步减均值之后,其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度(0~100),一个是汽车的座位数(2~6),显然第二个的方差比第一个小。因此,如果样本特征中存在这种情况,那么在第一步之后,求每个特征的标准差σ,然后对每个样例在该特征下的数据除以σ。
归纳一下,使用之前熟悉的表示方法,在求协方差之前的步骤是:
①
②![]()
③![]()
④![]()
其中,x(i)是样例,共m个,每个样例n个特征,也就是说x(i)是n维向量;![]() 是第i个样例的第j个特征;μ是样例均值;σj是第j个特征的标准差。
是第i个样例的第j个特征;μ是样例均值;σj是第j个特征的标准差。
相关文章

1985年,Seaman 和Curran 采用统计平均的方法,建立了模拟准脆性材料动态拉伸断裂与破碎的微裂纹细观损伤模型,得到了岩石材料在加载过程中的裂纹尺寸及分布的演化[14]。在此基础上,Matheson[20~23]提出了损伤与化学反应耦合模型 。CDAR 模型包括一个黏弹塑性模块和一个拉伸损伤膨胀模块,可以描述含能材料内部脱黏颗粒附近孔洞变化以及黏结剂开裂产生的微裂纹的张开和闭合。塑性体积膨胀应变率表示为......
2025-09-29

图4.2-60 提取进口总压对话框图4.2-61 提取转子部件转矩对话框表4.2-1 提取转子部件扭矩的面这里首先要讲的是轴向力的提取步骤,通过轴向力的提取,分析设计是否合理。图4.2-63所示为后处理得到的性能曲线及设计参数的对照。图4.2-64 后处理几何体一般在计算后,首先要提取进出口压强、叶轮转矩等,从而计算出整个泵的单机及整机的扬程、功率、效率等结果,对比设计工况和真实实验值,从而判断数值模拟的正确与否。......
2025-09-29

如第2章2.3.3节所述,面矩作为一种全局信息,已经广泛用于完全分割后的目标识别,其具有前面所述的整体特征的优缺点。当对边缘曲线进行尺度变化时,尺度的变化导致曲线长度的变化,相应的变化因子是k。此时尺度变化后的中心矩成为μ′pq=μpq×kp+q+1。为此,对7个不变矩进行如下修正,以调整其取值范围:式中所进行的修正变换应综合考虑不变矩特征的大小及后续识别的结构特点。......
2025-09-29

河流中悬移质泥沙的测验主要是测定水流中的含沙量,推求输沙率、断面平均含沙量等。图X2.15某站单沙与断沙关系水文年鉴中刊布成果有逐日平均悬移质输沙率表、逐日平均含沙量表、洪水水文要素摘录表中的含沙量过程摘录以及实测输沙率成果表等。......
2025-09-29

淬火工件分类便于选择材料、制订热处理的工艺方法,考核热处理技术经济指标。以工件的尺寸分类 有效尺寸不大于100mm的零件为薄件,大于100mm的零件为厚件。中淬透性钢件 这类钢的热处理淬火临界尺寸在60mm以下,常选用油冷淬火,对于大于这个尺寸的工件需要采用水—油双液淬火来达到技术要求。......
2025-09-29

模型用于待建工程计算前,应进行天然河道率定。最大输沙率计算值为0.16615kg/s,发生在7920s,沙峰试验值较计算值滞后。最大输沙率试验值与计算值之比1.69。验证计算结果见图9-25。......
2025-09-29

完成整体网格的划分并检查没有错误后,就可以把ICEM中导出的.cfx5文件导入CFX中,可以进一步检查几何体网格的划分正确与否。方法如下:1.导入网格文件1)选择→→→→,打开软件以后,首先定义工作目录,然后打开前处理组件,操作如图4.2-46所示。图4.2-46 前处理选项图4.2-47 前处理选择对话框4)全部导入网格后,网格的装配图如图4.2-48所示。图4.2-48 网格装配图4.2-49 命名域窗口2.生成域导入网格成功后,需要对输入的网格定义流动域和边界条件,操作如下。......
2025-09-29

涂层厚度的检测包括局部厚度的检测和平均厚度的检测。热喷涂涂层无损检测方法主要有磁性法、涡流法、测量法等,破坏性检测法主要有金相显微镜法。根据被测工件涂层有效面积的大小,采用不同测量点数进行。对于不同用途的涂层,可根据用户要求报告平均厚度、最小厚度或最大厚度。......
2025-09-29
相关推荐