稀疏编码算法：无监督学习与超完备基向量分析

2023-06-28 理论教育版权反馈

【摘要】：+|an|）这种方法被称为稀疏编码。要求系数ai是稀疏的意思就是说，对于一组输入向量，只想有尽可能少的几个系数远大于零。稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。因此，在稀疏编码算法中，另加了一个评判标准“稀疏性”来解决因超完备而导致的退化问题。稀疏编码分为两个部分。

如果把输出必须和输入相等的限制放松，同时利用线性代数中基的概念，即O=a1Ф1+a2Ф2+…+anФn，Фi是基，ai是系数，可以得到这样一个优化问题：

Min|I-O|

其中，I表示输入，O表示输出。

通过求解这个最优化式子，我们可以求得系数ai和基Фi，这些系数和基就是输入的另外一种近似表达。

pagenumber_ebook=174,pagenumber_book=158

因此，它们可以用来表达输入I，这个过程也是自动学习得到的。如果在上述式子上加上L1的Regularity限制，得到：

Min|I-O|+u（|a1|+|a2|+…+|an|）

这种方法被称为稀疏编码（sparse coding）。通俗地说，就是将一个信号表示为一组基的线性组合，而且要求只需要较少的几个基就可以将信号表示出来。“稀疏性”定义为：只有很少的几个非零元素或只有很少的几个远大于零的元素。要求系数ai是稀疏的意思就是说，对于一组输入向量，只想有尽可能少的几个系数远大于零。选择使用具有稀疏性的分量来表示输入数据是有原因的，因为绝大多数的感官数据，比如自然图像，可以被表示成少量基本元素的叠加，在图像中这些基本元素可以是面或者线。同时，比如与初级视觉皮层的类比过程也因此得到了提升，人脑有大量的神经元，但对于某些图像或者边缘只有很少的神经元兴奋，其他都处于抑制状态。

稀疏编码算法是一种无监督学习方法，它用来寻找一组“超完备”基向量来更高效地表示样本数据。虽然形如主成分分析（principal component analysis，PCA）技术能方便地找到一组“完备”基向量，但是这里想要做的是找到一组“超完备”基向量来表示输入向量，基向量的个数比输入向量的维数要大。超完备基的好处是它们能更有效地找出隐含在输入数据内部的结构与模式。然而，对于超完备基来说，系数ai不再由输入向量唯一确定。因此，在稀疏编码算法中，另加了一个评判标准“稀疏性”来解决因超完备而导致的退化（degeneracy）问题。

比如在图像特征提取的最底层要做边缘检测器的生成，那么这里的工作就是从原始图片中随机选取一些小块，通过这些小块生成能够描述他们的“基”，如图7-2右边的8×8=64个主成分组成的主成分，然后给定一个测试小块，可以按照上面的式子通过主成分的线性组合得到，而稀疏矩阵就是a，a中有64个维度，其中非零项只有3个，故称“稀疏”。

把底层作为边缘检测器，不同方向的边缘能够描述出整幅图像，所以不同方向的边缘自然就是图像的主成分了，而上上层又是上一层的组合主成分。

稀疏编码分为两个部分。

1）训练阶段：给定一系列的样本图片［x1，x2，…］，需要学习得到一组基［Ф1，Ф2，…］，也就是字典。

稀疏编码是k-means算法的变体，其训练过程也差不多，最大期望（expectation maximization，EM）算法的思想：如果要优化的目标函数包含两个变量，如L（W，B），那么可以先固定W，调整B使得L最小，然后再固定B，调整W使L最小，这样迭代交替，不断将L推向最小值。训练过程就是一个重复迭代的过程，按上面所说，交替的更改a和Ф使得下面这个目标函数最小。

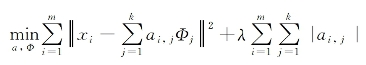
pagenumber_ebook=175,pagenumber_book=159

每次迭代分两步：

①固定字典Ф［k］，然后调整a［k］，使得上式，即目标函数最小，即解最小绝对收缩和选择算法（least absolute shrinkage and selection operator，LASSO）问题。

②固定住a［k］，调整Ф［k］，使得上式即目标函数最小，即解凸二次规划（quadratic programming，QP）问题。

不断迭代，直至收敛。这样就可以得到一组可以良好表示这一系列x的基，也就是字典。

2）编码阶段：给定一个新的图片x，由上面得到的字典，通过解一个LASSO问题得到稀疏向量a。这个稀疏向量就是这个输入向量x的一个稀疏表达。

稀疏编码算法：无监督学习与超完备基向量分析

相关推荐