由线性判别函数的设计过程可知，对于线性可分集，总能找到使模式样本正确划分的解。d维空间中线性判别函数的一般形式为g=ωX+b，分类面方程为：ωX+b=0将判别函数进行归一化，使两类所有样本都满足|g|＞1，这样分类间隔就等于2/‖ω‖。对于线性不可分问题，可以用类似于广义线性判别函数的方法，通过事先选择好的非线性映射将输入模式向量映射到一个高维空间，在这个空间中构造最优分界超平面。......
2023-06-16
支持向量机优化算法
【摘要】：支持向量机是机器学习中的一项新技术，是借助于最优化方法来解决机器学习问题的新工具，开始成为克服维数灾难和过学习等困难的强有力的手段。支持向量机方法建立在统计学理论的VC维理论和结构风险最小原理基础之上，根据有限样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的推广能力。支持向量机正是这样一种努力最小化结构风险的算法。这个归一化的结果便是支持向量机的几何间隔。
随着科学技术的飞速发展，以及计算机、互联网的日益普及，越来越多的复杂、非线性、高维度数据需要进行分析和处理，这无疑对传统的统计学方法提出了严峻的挑战。
从数据中发现知识是分析复杂数据、建立决策系统的基石，而模式分析和回归分析则是知识发现中的重要内容，也是处理许多其他问题的核心。支持向量机是机器学习中的一项新技术，是借助于最优化方法来解决机器学习问题的新工具，开始成为克服维数灾难和过学习等困难的强有力的手段。它在解决小样本、非线性及高维度模式识别中表现出许多优势，并能够推广应用到函数拟合等其他机器学习问题中。
传统统计学研究的内容是样本无穷大时的渐进理论，即当样本数据趋于无穷多时的统计性质，而实际问题中的样本数据往往是有限的。因此，假设样本数据无穷多，并依此为基础推导出的各种算法很难在样本数据有限时取得理想的应用效果。当样本数据有限时，本来具有良好学习能力的学习机器有可能表现出很差的泛化能力。
支持向量机方法建立在统计学理论的VC维理论和结构风险最小原理基础之上，根据有限样本在模型的复杂性和学习能力之间寻求最佳折中，以期获得最好的推广能力。其中，模型的复杂性指对特定训练样本的学习精度，学习能力是指无错误地识别任意样本的能力。
支持向量机的定义是，根据给定的训练集：
T=｛（x1，y1），（x2，y2），…，（xl，yl）｝∈（X×Y）l
其中，xi∈X=Rn，X称为输入空间，输入空间中的每一个点xi由n个属性特征组成，yi∈Y=｛-1，1｝，i=1，…，l。寻找Rn上的一个实值函数g（x），以便用分类函数：
f（x）=sgn（g（x））
推断任意一个模式x相对应的y的值的问题为分类问题。
在介绍结构风险最小（structural riskminimization）原理之前，首先对机器学习的本质做简要介绍。
机器学习本质上就是一种对所研究问题真实模型的逼近，通常会假设一个近似模型，然后根据适当的原理将这个近似模型不断逼近真实模型。毫无疑问的是，真实模型一定是不知道的，所以所选择的近似模型与真实模型之间究竟有多大的差距也就无从得知了，这也就引进了结构风险最小原理。
这个近似模型与真实模型之间的误差，通常称之为风险。在选择出一个近似模型之后，由于真实模型的未知性，所以真实误差也就无从得知，但是可以用某些可以掌握的量来逼近它。最直观的想法就是使用分类器在样本数据上的分类结果与真实结果之间的差值来表示，这个差值统计上称之为经验风险Remp（W）。
在过去的机器学习方法中，通常将经验风险最小化作为努力的目标，但是在实际的使用过程中却看到了这一方法的不足。通常很多分类函数能够在样本集上轻易达到百分之百的正确率，但是在投入实际具体问题中后却是错误百出，即模型无推广能力。在出现上述问题后，大家不难发现，由于所取得的样本数相对于现实世界的总体来说是非常渺小的，经验风险最小化原则只在占很小比例的样本上做到没有误差，但不能保证在更大比例的实际总体上也没有误差，所以这便是使用经验风险最小化原则建立的模型无推广能力的原因。
统计学习因而引入了泛化误差界的概念。所谓泛化误差界是指真实风险应该由两部分内容刻画：一是经验风险，代表了分类器在给定样本上的误差；二是置信风险，代表了我们在多大程度上可以信任分类器在未知样本上分类的结果。
泛化误差界的公式表示如下：
R（W）≤Remp（W）+φ（n/h）
式中，R（W）是真实风险，Remp（W）是经验风险，φ（n/h）是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险之和最小化，即结构风险最小化。
支持向量机正是这样一种努力最小化结构风险的算法。
在了解函数间隔及接下来将要介绍的几何间隔之前，首先应了解Logistic回归所使用的回归模型，通过对Logistic回归模型的相应替换，得到支持向量机模型，并讨论支持向量机模型中的函数间隔及几何间隔。
在支持向量机模型中使用的结果标签是y=-1和y=1，以此替换在Logistic回归中使用的y=0和y=1；同时将系数θ替换由W和b表示，即以前的θTx=θ0+θ1x1+θ2x2+…+θnxn（认为x0=1），替换θ0为b，后面的θ1x1+θ2x2+…+θnxn替换为w1x1+w2x2+…+wnxn（即wTx）。这样，让θTx=wTx+b，进一步hθ（x）=g（θTx）=g（wTx+b）。也就是说，除了y由y=0变为y=-1，只是标记不同外，与Logistic回归的形式化表示没有区别。
再明确一下假设函数：
hθ，b（x）=g（wTx+b），令Z=wTx+b
对于这个假设函数，我们只需要考虑θTx的正负问题，而不用关心g（z），因此这里将g（z）做一个简化，将其简单映射到y=-1和y=1上。映射关系如下：
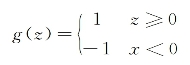
给定一个训练样本（x（i），y（i）），x是特征变量，y是结果标签，i表示第i个样本。定义函数间隔如下：
刚刚定义的函数间隔是针对某一个样本的，现在定义全局样本函数间隔如下：
其中，i=1，…，m。
其实，对于函数间隔最直接的看法就是在训练样本上分类正例和负例确信度最小的那个函数间隔。
针对上述函数间隔的介绍，继续考虑W和b，如果同时加大W和b，比如在（WTx（i）+b）前面乘个系数，假设乘以2，那么所有点的函数间隔都会增大变为原来的两倍，这对求解问题是不会产生影响的，因为要求解的是WTx（i）+b=0，同时扩大W和b对结果是无影响的。这样，为了限制W和b，可能需要加入归一化条件，毕竟求解的目标是确定唯一一组W和b，而不是多组线性相关的向量。这个归一化的结果便是支持向量机的几何间隔。
由此可以得到支持向量机几何间隔的定义如下：
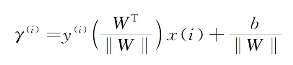
由几何间隔的定义式可以看出，当‖W‖=1时，几何间隔便等于函数间隔。所以，无论W和b同时扩大多少倍，‖W‖都会跟随W和b同步扩大相同倍数，从而对结果无影响。所以可以定义全局的几何间隔为：
γ=min（γ（i））
其中，i=1，…，m。
之前讨论的情况都是建立在样例线性可分的假设上，当样例线性不可分时，可以尝试使用核函数来将特征映射到高维，这样很可能就可分了。正如图6-9中所示，原始特征是线性不可分的，但是通过对原始特征进行高斯变换后，得到的新特征就是线性可分的了，这便是对核函数最直接的理解。
图6-9 高斯核函数对数据的转换
所以可以将核函数形式化的定义为：如果原始特征内积是（x，z），映射后为［φ（x），φ（z）］，那么核函数为：
K（x，z）=φ（x）Tφ（z）
有关工业智能技术与应用的文章
- 详细阅读
-
支持向量机分类器的应用介绍详细阅读
支持向量机是Vapnik及其合作者［130］根据结构风险最小化原则提出的一种在高维特征空间使用线性函数假设空间的学习系统。支持向量机是机器学习领域若干标准技术的集大成者。在若干挑战性的应用中，获得了目前为止最好的性能。，xn)′标记为正类，否则，将其标记为负类。图3-4 二维训练集的分开超平面(w,b)图3-5 最优超平面对于多个模式类的分类问题，输出域是Y={1，2，…......
2023-06-28
-
桥梁可靠度分析方法应用：支持向量回归详细阅读
支持向量机是由Vapnik［7］提出的一种机器学习方法，主要有支持向量分类和支持向量回归两种算法。由于SVR是目前结构可靠度分析中的一种较为新颖的方法，下文将简单介绍SVR在结构响应函数拟合应用中的相关理论。SVR学习理论主要是通过如式（3.2）所示的ε敏感函数［8］来控制SVR模型的拟合误差。由式（3.5）可得到SVR模型的函数表达式：为了提高建立SVR模型的效率与精度，可通过对输入样本点及SVR模型参数进行优化。......
2023-09-19
-
量子遗传优化算法的优化方法详细阅读
量子遗传算法是一种将遗传算法和量子计算相结合的概率优化方法，两者相互作用。量子遗传算法是一种将量子比特的概率幅用于染色体编码，用量子门的调整操作来实现染色体更新，以完成进化搜索的方法。量子遗传算法的流程如下：初始化种群Q，随机生成n个用量子比特编码的染色体。......
2023-06-29
-
模拟退火算法优化详细阅读
模拟退火算法是由N Metropolis等学者于1953年最早提出的。模拟退火算法从某一给定的初始温度开始，随着迭代的进行，温度参数不断下降，结合算法概率性的突跳能力在问题的可行解空间中随机寻找目标函数的解，并以Metropolis准则判定是否接受新解，如此迭代进行下去，逐步寻找问题的全局最优解。Metropolis接受准则是模拟退火算法的重要核心思想，Metropolis接受准则也是依据固体物质退火过程的特点而提出的。图11-2模拟退火算法流程图③算法运算产生新解。......
2023-06-28
-
混沌粒子群优化算法优化方案探究详细阅读
混沌粒子群优化算法的基本思想是采用混沌序列初始化粒子的位置和速度,先对当前粒子群体中的最优粒子进行混沌寻优,然后把混沌寻优的结果随机替换粒子群体中的一个粒子。,z1N),根据式(4-6)得到N个向量z1,z2,…如果粒子适应度优于全局极值gbest,则将gbest设置为新位置。则混沌粒子群优化算法的流程为:初始化,设置最大允许迭代次数或适应误差限,以及CPSO算法的参数惯性权值和学习因子。,PgD)进行混沌优化:将Pgi(i=1,2,…计算其适应值,得到性能最好的可行解pb。......
2023-06-23
-
熔透控制算法优化方案详细阅读
在TIG焊熔透控制系统中，控制器采用的是模糊PID控制方法，这种控制系统在焊接过程中具有自校正控制的功能。熔透控制是在起弧稳定后开始的，为了保证控制的准确性，取前10个周期的熔宽平均值作为整个控制过程的熔宽参考值。根据这些控制规则，再按照模糊控制推理合成规则进行运算，采用最大隶属度方法进行模糊判决，经过多次的试验和修改，得到最终的模糊控制表。......
2023-06-26
-
遗传算法优化问题求解详细阅读
遗传算法的这些性质，已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。遗传算法之所以具备强大的搜索能力，是因为包罗了选择、杂交和变异三种基本操作算子，同时这三种操作算子也是模拟自然生物圈中自然存在的有性繁殖、杂交和变异等现象的核心载体。同样，遗传算法中起核心作用的是遗传操作的交叉算子。通过交叉，遗传算法的搜索能力得以飞跃提高。图11-1遗传算法流程图......
2023-06-28
相关推荐