聚类分析：机器学习中的热点技术

2023-06-28 理论教育版权反馈

【摘要】：聚类分析是一种原理简单、应用广泛的机器学习技术。聚类分析已成为机器学习研究中的一个热点。图6-3k-均值聚类算法步骤示例k-中心点聚类k-中心点算法与k-均值算法在原理上十分相近，它是针对k-均值算法易受极值影响这一缺点的改进算法。以密度聚类算法来详细说明，该方法将“簇”看作是数据空间中被低密度区域分割开的“稠密区域”，即密度相连样本点的最大集合。图6-7期望最大化聚类算法步骤示例

聚类分析是一种原理简单、应用广泛的机器学习技术。聚类分析就是把若干事物按照某种标准归为几个类别，其中较为相近的聚为一类，不那么相近的聚于不同类。

聚类分析在客户分类、文本分类、基因识别、空间数据处理、卫星图片分析、医疗图像自动检测等领域有着广泛的应用。聚类分析的研究是一个蓬勃发展的领域，数据挖掘、统计学、机器学习、空间数据库技术、生物学和市场学也推动了聚类分析研究的进展。聚类分析已成为机器学习研究中的一个热点。

聚类算法种类繁多，本节将选取普及性最广、最实用、最具有代表性的5种聚类算法进行介绍，其中包括：

●k-均值聚类（k-means）；

●k-中心点聚类（k-medoids）；

●密度聚类（densit-based spatial clustering of application with noise，DBSCAN）；

●系谱聚类（hierarchical clustering，HC）；

●期望最大化聚类（expectation maximization，EM）。

需要说明的是，这些算法本身无所谓优劣，最终运用于数据的效果却存在好坏差异，这在很大程度上取决于数据使用者对于算法的选择是否得当。本节我们将对这5种算法的基本原理和各自的特点进行简要介绍，并以图示方式辅助理解来指导算法选择。

（1）k-均值聚类

k-均值聚类算法是最早出现的聚类分析算法之一，它是一种快速聚类方法，但对于异常值或极值敏感，稳定性差，因此较适合处理分布集中的大样本数据集。

k-均值聚类的思路是以随机选取的A（预设类别数）个样本作为起始中心点，将其余样本归入相似度最高中心点所在的簇（cluster），再确立当前簇中样本坐标的均值为新的中心点，依次循环迭代下去，直至所有样本所属类别不再变动。算法的计算过程非常直观，图6-3所示为以将10个点聚为3类为例展示算法步骤。

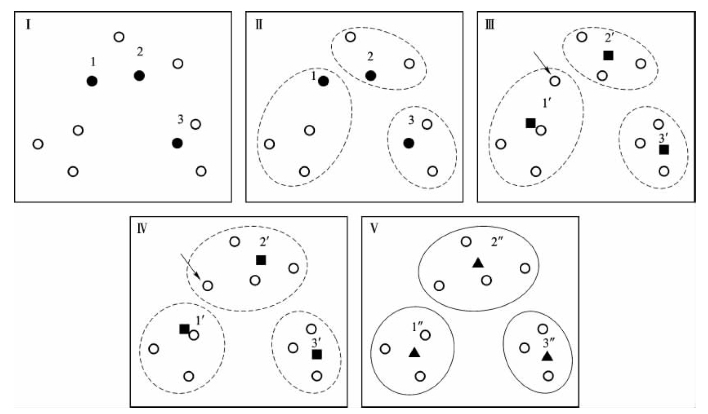
pagenumber_ebook=145,pagenumber_book=129

图6-3　k-均值聚类算法步骤示例

（2）k-中心点聚类

k-中心点算法与k-均值算法在原理上十分相近，它是针对k-均值算法易受极值影响这一缺点的改进算法。在原理上的差异在于选择各类别中心点时不取样本均值点，而在类别内选取到其余样本距离之和最小的样本为中心。

图6-4所示为该算法的基本运行步骤。

pagenumber_ebook=145,pagenumber_book=129

图6-4　k-中心点聚类算法步骤示例

（3）系谱聚类

系谱聚类的过程可以通过类似于系谱图的形式呈现出来。相对于k-均值算法与k-中心点算法，系谱算法的突出特点在于不需事先设定类别数k，这是因为它每次迭代过程仅将距离最近的两个样本/族聚为一类，其运作过程将自然得到k=1至k=n（n为待分类样本总数）个类别的聚类结果，如图6-5所示。

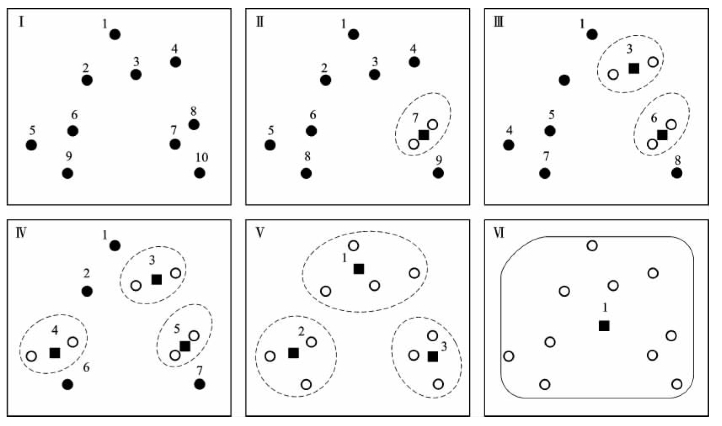
pagenumber_ebook=146,pagenumber_book=130

图6-5　系谱聚类算法步骤示例

（4）密度聚类

密度聚类算法是基于密度的聚类方法中最常用的代表算法之一，另外还有OPTICS算法、DENCLUE算法等，读者可自行学习。

基于密度的聚类算法相对于如前所说的k-均值、k-中心点，以及系谱聚类这些基于距离的聚类算法，其优势在于弥补了它们只能发现“类圆形”聚类簇的缺陷，该类算法由于是基于“密度”来聚类的，可以在具有噪声的空间数据库中发现任意形状的簇。

以密度聚类算法来详细说明，该方法将“簇”看作是数据空间中被低密度区域分割开的“稠密区域”，即密度相连样本点的最大集合。为了理解其思想，可参照图6-6来说明算法步骤，首先应明确其输入值为待聚类数据集、半径E（即为图中各圆形的半径大小）与密度阈值MinPts（图中取3），具体步骤如下：

①从数据集中选择一个未处理的样本点，如我们第一次选择图Ⅰ中的点1；

②以点1为圆心，作半径为E的圆，由于圆内圈入点的个数为3，满足密度阈值MinPts，因此称点1为核心对象（用黑色实心圆点表示），且将圈内的4个点形成一个簇，其中点1直接密度可达周围的3个灰色实心圆点；

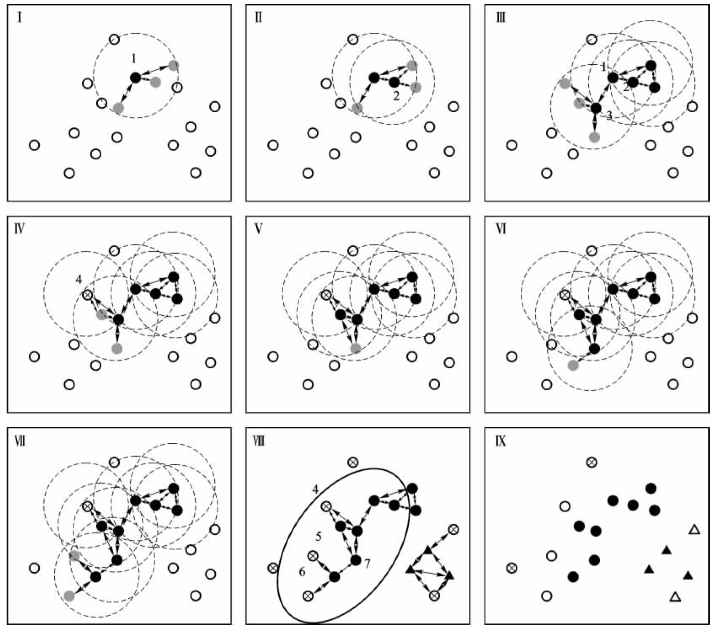
pagenumber_ebook=147,pagenumber_book=131

图6-6　密度聚类算法步骤示例

③同理考察其他样本点，重复步骤②若干次，得到图Ⅲ，其中点1直接密度可达核心对象3，且点2密度可达点3；

④当该过程进行到图Ⅳ，我们发现点4的E邻域内仅有2个点，小于阈值MinPts，因此，点4为边缘点（非核心对象），暂标记为，然后继续考察其他点；

⑤当所有对象都被考察，该过程结束，得到图Ⅷ，看到椭圆形内有若干核心对象和边缘点，这些点都是密度相连的；

⑥最后一步即为将各点归类，见图Ⅸ，点集●相互密度可达，属于类别1，点集▲相互密度可达，属于新的一类，记类别2；点集○与类别1样本点密度相连，属于类别3；点集A与类别2样本点密度相连，属于类别4；点⊕即非核心对象，也不与其他样本点密度相连，为噪声点。

密度聚类算法的不足之处在于，它对于用户定义参数半径E及密度阈值MinPts很敏感，参数取值细微的不同可能会导致差别很大的结果，而且参数的选取无规律可循，只能不断尝试靠经验确定。

（5）期望最大化聚类

期望最大化算法的思路十分巧妙，在使用该算法进行聚类时，它将数据集看作一个含有隐性变量的概率模型，并以实现模型最优化，即获取与数据本身性质最契合的聚类方式为目的，通过“反复估计”模型参数找出最优解，同时给出相应的最优类别数而“反复估计”的过程即是期望最大化算法的精华所在，这一过程由E-step（expectation）和M-step（maximization）这两个步骤交替进行来实现。

该算法相比于前面介绍的几种聚类算法更为抽象，图6-7中，图Ⅱ是对图Ⅰ中的10个样本点随机聚类的初始结果，可以明显看到聚类效果很差；随后进行第一、二次迭代，聚类结果分别如图Ⅲ、图Ⅳ所示，每一次都比前一次更契合数据，至图V完成第三次迭代，聚类结束。

pagenumber_ebook=148,pagenumber_book=132

图6-7　期望最大化聚类算法步骤示例

聚类分析：机器学习中的热点技术

相关推荐