kNN算法详解

2023-06-28 理论教育版权反馈

【摘要】：kNN算法最初由Cover和Hart于1968年提出的，是最近邻算法的一种推广，广泛应用于机器学习和数据分类。因此，kNN算法不具有显式学习的过程，而是利用样本集对向量空间进行划分。图6-2k值选取分类效果kNN算法中影响算法准确率的因素有距离函数和k值的选择，图6-2为选取不同k值分类的效果图。

kNN算法最初由Cover和Hart于1968年提出的，是最近邻算法的一种推广，广泛应用于机器学习和数据分类。kNN算法是一种基于向量空间模型的预测性分类算法，通过计算向量之间的距离来确定待检测样本的类别。kNN算法的核心思想是：如果一个待检测样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。因此，kNN算法不具有显式学习的过程，而是利用样本集对向量空间进行划分。kNN算法原理如下。

输入：样本集

T=｛（x1，y1），（x2，y2），…，（xn，yn）｝

其中，xi∈X⊆T为样本集的特征向量；

yi∈Y=｛c1，c2，…，cn｝为样本的类别；

i=1，2，…，N；

X为待检测样本的特征向量。

输出：待检测样本所属类别y。

①根据选取的距离函数，在样本集T中找出与x最近距离的k个点，这k个点的邻域记作Nk（x）；

②在Nk（x）中根据多数表决的判定规则，判断x的类别y；

pagenumber_ebook=143,pagenumber_book=127

式中I为指示函数，k为近邻个数，即当yi=cj时，I=1。

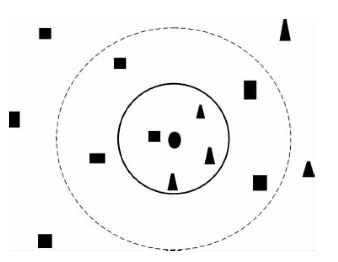
pagenumber_ebook=143,pagenumber_book=127

图6-2　k值选取分类效果

kNN算法中影响算法准确率的因素有距离函数和k值的选择，图6-2为选取不同k值分类的效果图。

样本集共两类：四方形和三角形，图中测试样本是圆形。运用kNN分类算法时，不同的k值影响分类结果：当k=1时，离其最近的一个样本是四方形，圆被判定为四方形一类；当k=4时，离其最近的四个样本中，三角形占3/4，圆被归为三角形一类；当k=8时，离其最近的8个样本中，四方形占5/8，圆被归为四方形一类。这就是对kNN分类原理的一个直观描述，也说明k值的选择直接影响分类的准确性。

kNN算法在处理大数据样本时是一种较好的分类算法，主要优点有：

①思路简单直观，方便实现，准确率高，传统的kNN算法无需对样本训练；

②没有过多的数据规则需要描述，分类过程直接利用样本与样本之间距离的关系，避免了其他因素对结果的影响，可以大幅减少误差，体现了分类规则独立性，特别适合类别特征不明显的分类问题；

③在执行分类的过程中只与少量的k个最相邻样本相关，特别适合多类别、大样本数据的分类计算。

kNN方法的不足之处主要有：

①对样本集依赖性较强，样本集中样本的多少以及样本类别的多少都会影响到kNN算法在实际的应用，由于在确定分类决策上只依据最邻近几个样本类别来决定待检测样本所属的类别，当样本不平衡，如一类样本容量很大，而其他类样本容量很小时，有可能导致造成不论k值多大，k个邻居样本大多数属于大容量类的，计算分类结果缺乏说服力；

②分类速度慢，kNN算法在进行分类计算时，是按照距离函数逐一计算待分类样本与样本集中的样本的距离，然后根据距离的大小进行分类，当样本的维数和规模比较大时，算法的复杂度较高，导致分类速度大幅度降低；

③k值的选择，由于kNN算法中几乎所有的计算都发生在分类阶段，而k值的大小直接关系到最终的分类准确率，一般情况下，k越大，分类的结果越准确；但是如果k值选择过大，且样本集较小时，会增加计算量，导致分类准确率下降；k值选择过小，得到的近邻数过少，也会降低分类精度；k值没有确定公式，一般通过人工取多个k值进行多次训练，取分类结果误差最小的k值。

kNN算法详解

相关推荐