在风电场并网研究中所关注的是风力机的尾流模型，有一维尾流模型和三维尾流模型[31]。自20世纪起，专家们建立了多种风力机一维尾流模型。目前在风电场并网研究中，很多专家采用Jensen尾流模型研究风力机的尾流特性[36-41]。图1-5 AV尾流模型图1-6 风电机组排列布置在风电场内，尾流效应造成风电场内每台风力机的输入风速不同，并且受风力机的风轮直径、推力系数、机组间的距离、周围环境及风速和风向等因素的影响[42]。......
2023-06-28
AV尾流模型的研究及应用
【摘要】：AV尾流模型是在Abramovich射流理论基础上建立的一种全场尾流模型。因此，利用射流理论建立的风力机AV尾流模型就忽略了受风速切向分量影响的气流的横向速度分量。下面分别对AV尾流模型各个区域的尾流特性进行分析。
AV尾流模型是在Abramovich射流理论基础上建立的一种全场尾流模型。Abramovich自由射流中的流线模型如图4-2a所示[7]。由于射流与周围静止介质发生动量交换，而使四周连续不断地有流体进入射流混合区中，所以在射流边界处的横向速度的方向（y轴）流体从外面进入射流里面，从而靠近边界处的流线呈图4-2a所示的形状。实验与理论分析表明，与轴心纵向速度（x轴）相比，射流中的横向速度很小，因此在射流中接近轴心线区域的大部分流线几乎近于平行，从而在一般工程应用中，流线可作为平行直线看待。而在射流初始段核心区中，因为流动的对称性，所以在该区内的横向速度为零，从而在等速核心区中的流线是平行直线，如图4-2b所示。因此，利用射流理论建立的风力机AV尾流模型就忽略了受风速切向分量影响的气流的横向速度分量。
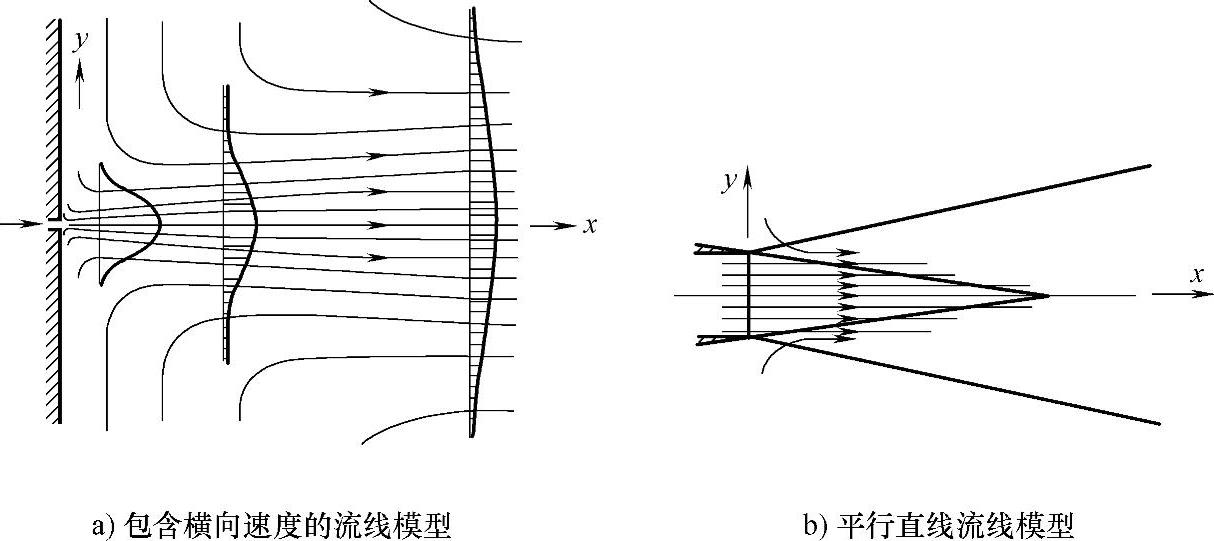
图4-2 射流流线模型
AV尾流模型如图4-3所示。AV尾流模型将风力机尾流区分成三个区域，初始尾流区（区域Ⅰ）、过渡区（区域Ⅱ）和远场尾流区（区域Ⅲ）。下面分别对AV尾流模型各个区域的尾流特性进行分析。
1.区域Ⅰ的尾流特性
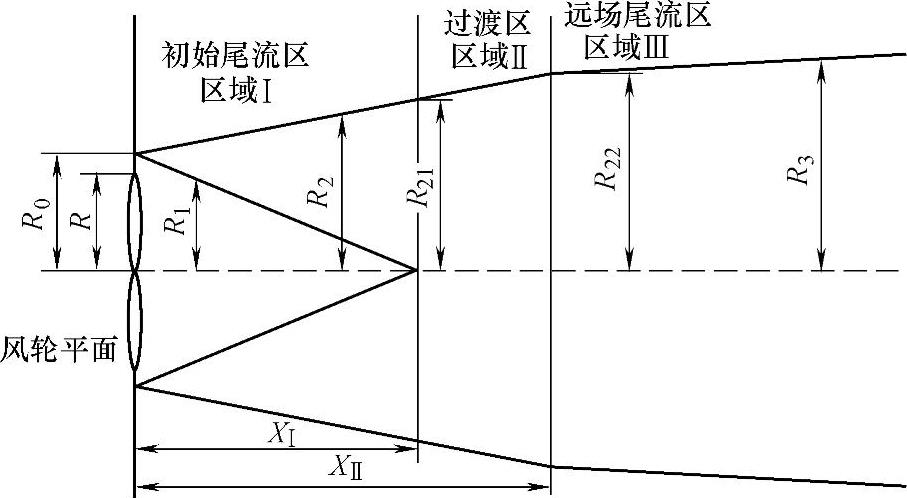
图4-3 AV尾流模型
区域Ⅰ是近场尾流区，从风轮旋转平面一直延伸到风轮后锥形均匀流的末端。这个区域的速度剖面随着由机械湍流和背景湍流组成混合区的相对大小变化而变化，其尾流增长速率取决于机械湍流，背景湍流也有一定的影响。
区域Ⅰ内自由流与风轮后锥形均匀流之间的距离可视为边界层厚度，用符号b表示，有
b=r2-r1 （4-7）
式中，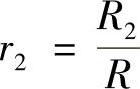
，
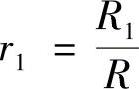，R为风轮半径（m），R1为风轮后锥形均匀流半径，R2为尾流半径。
在区域Ⅰ末，r1=0，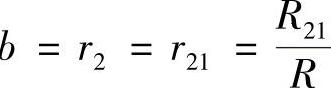
，R21为区域Ⅰ末的尾流半径，r21为区域Ⅰ末的无量纲尾流半径。
区域Ⅰ中，由于机械湍流引起的边界层增长率为
式中，x为风轮下游某点到风轮平面的轴向无量纲距离，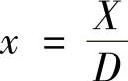
，其中X为风轮下游某点到风轮平面的轴向距离；xIm为与机械湍流相关的无量纲尾流长度，可表示为
式中，XIm为区域Ⅰ中与机械湍流强度相关的尾流长度（m）；r0为无量纲初始尾流半径，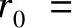
，其中R0为初始尾流半径，m为初始速度比，且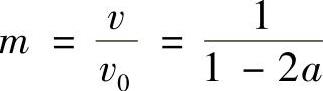
，a为轴向诱导因子，
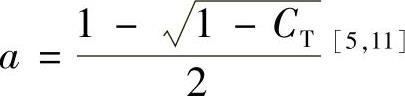，CT为风轮轴向推力系数，v为风力机输入风速，v0为风轮后锥形均匀流风速。
背景湍流引起的边界层增长速率α为
式中，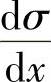
与大气层中Pasquill稳定级相关[8]。
在区域Ⅰ中，由于机械湍流和背景湍流同时存在，因此总的边界层增长速率为
区域Ⅰ的无量纲尾流总长度xI为
式中，区域Ⅰ末的无量纲尾流半径r21为
区域Ⅰ的无量纲尾流半径r2随x变化而变化，可表示为
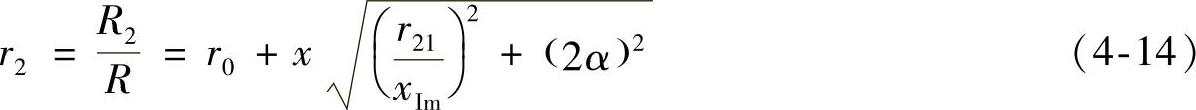
区域Ⅰ的尾流横向剖面上的无量纲速度可表示为
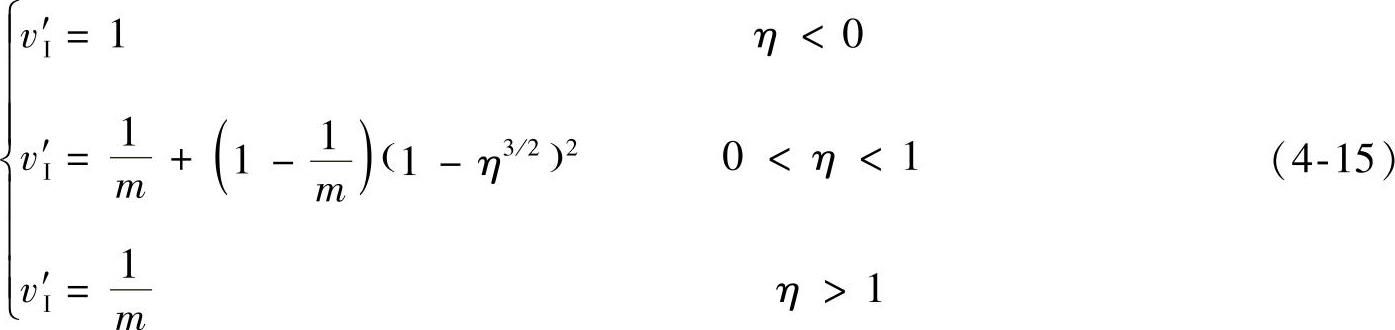
式中，
，r为尾流横向剖面上某点到尾流旋转轴的距离。
2.区域Ⅱ的尾流特性
区域Ⅱ是一个过渡区。区域Ⅱ同区域Ⅰ有相同的尾流增长速率，它主要决定于机械湍流和背景湍流。区域Ⅱ末的无量纲尾流长度xⅡ为
xⅡ =nxⅠ （4-16）
式中
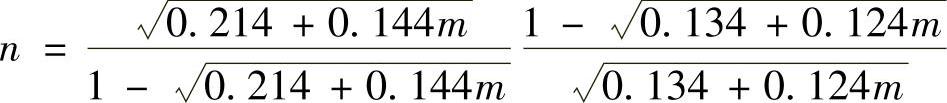
区域Ⅱ的尾流速率与区域Ⅰ一致，故区域Ⅱ的无量纲尾流半径r2为
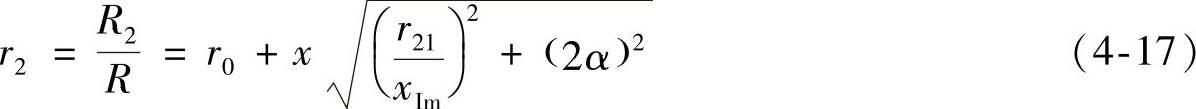
区域Ⅱ末的无量纲尾流半径r22为
r22=r0+n（r21-r0） （4-18）
区域Ⅱ的尾流横向剖面上的无量纲速度可表示为
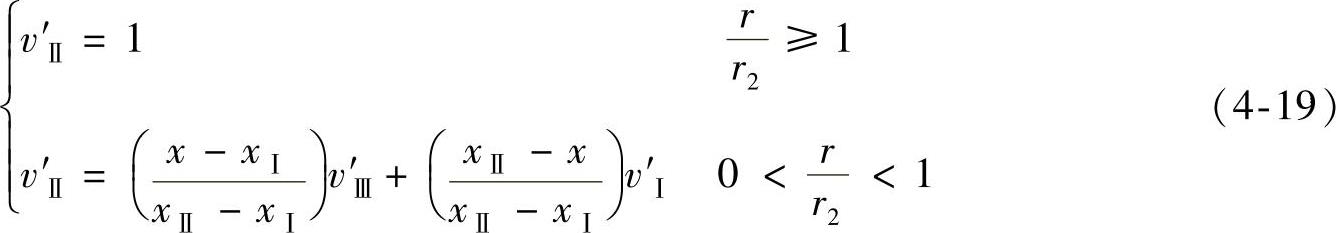
式中，v′Ⅰ、v′Ⅲ分别表示同一
值用于式（4-15）和式（4-23）计算所得的区域Ⅰ和区域Ⅲ的速度值。
3.区域Ⅲ的尾流特性
区域Ⅲ是远场尾流区。尾流增长速率在开始时是由机械湍流和背景湍流共同决定，随着X的增加，机械湍流的影响逐渐减小到零；然后背景湍流起主导作用。因此，区域Ⅲ中尾流边界层增长速率α可表示为
式中，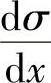
与大气层中Pasquill稳定级相关[8]。
区域Ⅲ的无量纲尾流半径r3为
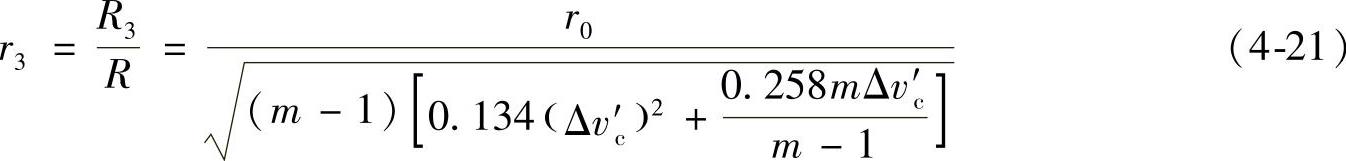
式中，R3为区域Ⅲ的尾流半径；Δv′c为尾流旋转轴上的无量纲速度损失系数，即
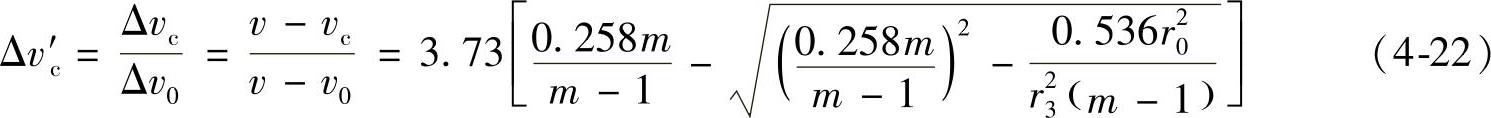
式中，v为风力机输入风速；v0为风轮后锥形均匀流风速；vc为风力机尾流区域内旋转轴上的风速。
区域Ⅲ的尾流横向剖面上的无量纲速度可表示为
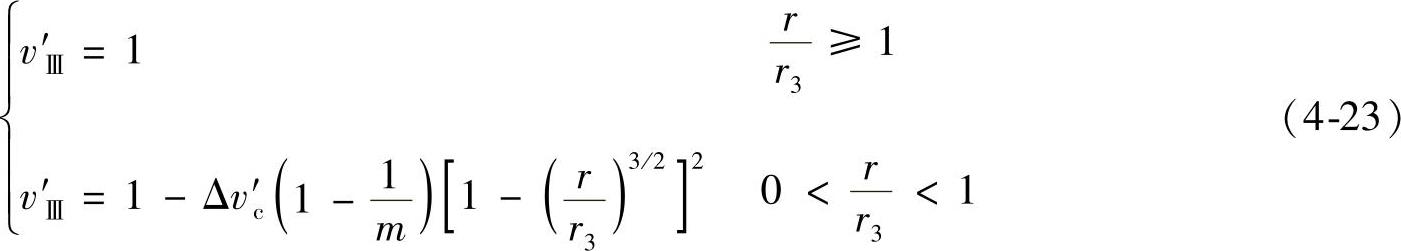
风经过风力机，风速突变减小，而后由于周围气流作用，风力机尾流区内风速会逐渐恢复。下面，利用下式定义的尾流区域内速度恢复率δ描述风电机组尾流区域内风速的变化：
式中，vn为风力机尾流区域内距风力机n倍风轮直径截面处的平均风速；v为风力机输入风速。
由以上介绍的几种尾流模型可以看出，无黏近场尾流模型、简化尾流模型、Jensen尾流模型都没有较为准确地描述风力机尾流效应的特点，而采用Abramovich射流理论建立的AV尾流模型能较为准确地模拟风力机尾流区的速度衰减和逐步恢复的过程。下面，本文将采用AV尾流模型研究风电场的尾流效应模型。
对于实际的风电场而言，气流经过风轮后产生的尾流区及尾流影响范围除了与来流风速、离开上游风轮的距离有关外，显然还与风向有关。风向变化时，风力机通过其偏航控制保持风轮对准风向，风力机的尾流区随风向变化[9]。鉴于此，下面首先建立单台风力机的AV尾流模型；然后考虑风电场内风电机组排列布置和风向变化，研究风电场尾流效应模型，确定风电场内风电机组的输入风速；最后考虑风速、风向波动，提出风电机组分组方法。
有关风电场建模技术及应用的文章
- 详细阅读
-
风电场模型优化及尾流效应分析详细阅读
对于实际风电场而言，由于尾流效应的影响，风电机组的输入风速存在差异，因此会导致风电机组工况不同。因此，对于装机容量较大的风电场，应考虑采用多台等效风电机组模拟风电场。在建立风电场多机组等效模型时，首先需要对风电机组分组，再对归为一组的风电机组进行等效，并考虑风电场内部馈线。......
2023-06-28
-
RLO-RAO应用模型：描述机制及应用研究详细阅读
RLO-RAO整合模型实现了学习对象和活动对象相互分离，活动层实现了学习活动的数字化描述与编排，在学习对象的描述和调用上可参照IMS的学习对象元数据标准。学习对象采用元数据的形式进行描述，同时将具体的Web网页、微视频等教学资源组织成可重用学习对象，供学习活动进行调用；每个学习活动是通过一个具体的学习工具进行链接，如在线帮助、头脑风暴等。学习对象的组成元素都可以使用元数据进行描述，以方便检索。......
2023-11-07
-
SLURP水文模型应用与研究详细阅读
3.1.1SLURP水文模型简介SLURP模型［4］是以日为时间步长，模拟从降水到径流的整个水文循环过程，具有物理机制的分布式水文模型。......
2023-06-26
-
数字孪生模型的创建及应用方法详细阅读
研究与实践表明，相关领域应用过程中所需解决的首个挑战是如何根据不同的应用对象与业务需求创建对应的数字孪生模型。目前通用的数字孪生参考模型与创建方法的指导的缺乏，严重阻碍了数字孪生在相关领域的落地应用。......
2023-10-30
-
NAG-FRAG模型优化及应用详细阅读
NAG－FRAG 模型是Seamen 等［8］提出来的，他们在用平板撞击技术研究脆性材料的动态断裂时发现，脆性材料的动态断裂过程是：微裂纹的成核、成长、聚合、形成碎片、断裂。赵锋等［9］在研究JO－9159 的冲击断裂和破碎中，对该模型进行了简化，在计算中将σg0近似取为常数。......
2023-06-27
-
TLM模型的特点及应用场景介绍详细阅读
旗袍是中国传统服装文化的经典，它拥有浓厚的民族特点和丰富的艺术语言。旗袍的美主要体现在造型、色彩、纹样、材质等元素中。这种含蓄的曲线充分显示了女性自然的美，同时也非常符合东方女性的体型；其次，旗袍造型的变化，主要是襟形、袖式和领型等的变化。女性一般可针对自己的脸型、身材来挑选旗袍的襟形。图4-2-7如意襟旗袍图5.6TLM 电流分布示意图......
2023-06-21
-
DeviceNet设备对象模型及应用技术详细阅读
DeviceNet规范中提供了公共服务和对象类的特定服务的描述，还提供了制造商特定服务的定义。DeviceNet的连接ID置于CAN的标识符区内。16）客户机：DeviceNet网络中的主站节点，它能主动发送显式请求报文。图7-14 DeviceNet对象模型对象大体上可以分为两类：通信对象和应用对象。这几个对象是每一个DeviceNet节点必须具有的对象。......
2023-11-20
相关推荐