由于企业安全支撑体系二级指标多为定性指标，可以采用德尔菲法进行评价，但是德尔菲法也有一些不可避免的缺陷，如意见的可靠程度、科学依据缺乏、评价周期较长等，因此对于指标权重以及指标分数的确定，可以采取乐观系数法进行修正。由此证明，该方法所得到的评估结果与实际应用情况基本相等，乐观系数估分法对于企业安全支撑体系指标体系评估中定性指标得分的准确获取，具有较好的实际意义。......
2023-06-28
关键因子筛选方法：石油企业安全平台的灰色关联评估
【摘要】：灰色关联评估法是一种基于灰色关联度理论对影响事物的多种灰色因素进行综合评价的方法。可见，灰色关联因子评估法可以应用在指标筛选方面，同时实践证明，其具有明显优势。根据这一思路，选择灰关联法进行研究。也可依此设计出简化的企业安全生产平台支撑体系评价模型。
1.灰色关联评估法
灰色系统理论由邓聚龙于1984年提出，它是一种解决系统中包含不完全与不确定信息的多准则理论，该理论现已广泛并成功地应用于各领域。
灰色关联评估法是一种基于灰色关联度理论对影响事物的多种灰色因素进行综合评价的方法。基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的灰关联度就越大，反之就越小。灰关联的分析方法就是通过计算系统特征变量数据序列与相关因素变量数据序列之间的灰关联度，建立起灰关联矩阵，利用优势分析原则，得出各影响因素的顺序，最终确定出主要影响因素，其具体分析过程如下。
（1）建立因子空间
设原始序列μi=（μi（1），μi（2），…，μi（n））为参考系列；ωj=（ωj（1），ωj（2），…，ωj（n））为比较系列。对这两个序列进行无单位处理，可以建立因子空间。这里我们对数据采取均值化处理，即通过均值化算子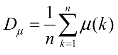
和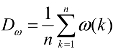
的作用求得各变量数据序列的均值相，则因子空间为
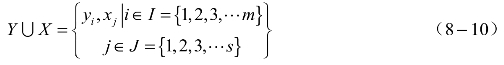
这里
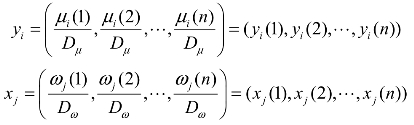
（2）计算灰关联系数γ（yi（k），xj（k））和灰关联度γ（yi，xj）
灰关联系数γ（yi（k），xj（k））是指比较序列对参考序列在k点的关联水平。灰关联系数的计算公式为
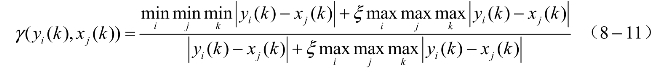
灰关联度的计算公式如下：
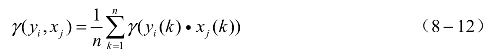
式中，k=l，2，…，n；
ξ——分辨系数，一般取0.5。
（3）建立灰关联矩阵，进行优势分析
利用式（8-12）得到灰色绝对关联矩阵为
当j∈J=（1，2，3，…，s），满足γ（yi，x1）＞γ（yi，xj），其中i∈I=（1，2，3，…，m），则认为对系统特征变量yi来说，因素x1优于因素xj。若对任意的j∈J=（1，2，3，…，s）都有x1优于xj，则x1为最优因素。若不存在最优因素，必然存在j∈J=（1，2，3，…，s）满足
那么，因素x1准优于因素xj。若对任意的j∈J=（1，2，3，…，s），x1均准优于因素，则称x1为准优因素。这里我们把最优因素和准优因素统称为优势因素。
可见，灰色关联因子评估法可以应用在指标筛选方面，同时实践证明，其具有明显优势。
2.关键安全特征因子筛选
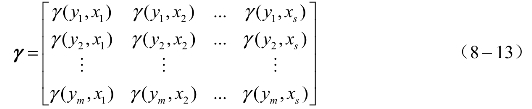
首先我们仍然用德尔菲法对16个指标进行初步筛选。随后剔除制度支撑体系一级指标下的安全文化氛围二级指标、组织支撑体系一级指标下的企业应急管理二级指标、技术支撑体系一级指标下的中介服务体系二级指标、成员支撑体系一级指标下的员工的文化素质二级指标，得到12个指标，如表8-3所示。
表8-3 初步筛选的12个指标
上述初选的12个安全特征指标，仍然不是最终的结果，只有那些与实际结果（安全绩效）密切相关的指标才是最终选择的指标。根据这一思路，选择灰关联法进行研究。通过计算系统特征变量数据序列（安全绩效）与相关因素变量数据序列（安全特征初选指标）之间的灰关联度，建立灰关联矩阵，利用优势分析原则，得出各影响因素的顺序，最终确定出主要影响因素，即最终的安全特征指标，称之为关键安全特征因子。对此运用实证的方法进行分析。
本书对8家企业（此处隐去单位真实名称）在2010年10月用12项安全特征指标进行打分评价。它们各项指标的得分值（ωi）以及其后2010年度安全绩效考核平均值（μ1）如表8-4所示。
表8-4 8家企业的指标得分值以及实际安全绩效考核平均值
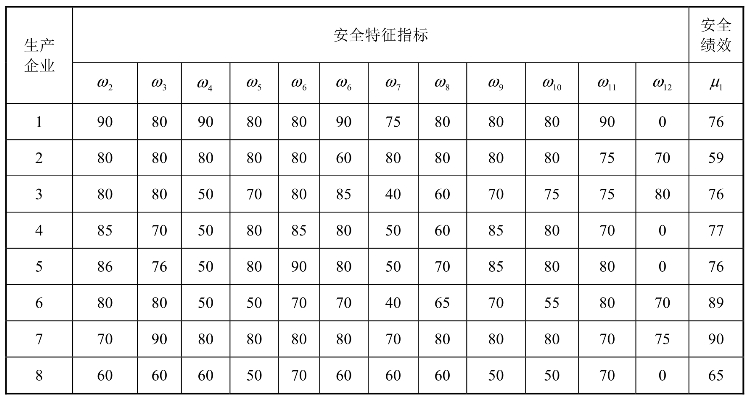
把μ1作为参考序列，而ωi（1=1，2，…，12）作为比较序列。具体分析过程如下所示。
（1）建立因子空间
（2）根据式（8-11）、式（8-12）计算
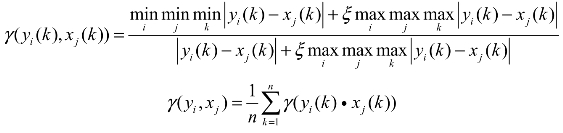
可得灰色关联矩阵
为便于理解，将灰色关联矩阵采用表形式表达，如表8-5所示。
表8-5 灰色关联矩阵
由灰色关联矩阵可以看出，因素变量中员工的安全意识、政府安全监管、培训宣教体系、安全制度规范、生产安全技术、员工的技术素质、安全生产环境、管理模式、企业安全管理对于安全绩效的影响具有明显相关性，它们分别排在1～9位，影响因子都在0.8以上。所以最终确定这9个指标为关键安全特征指标，分别按次序重新标注为
筛选结果也印证了企业安全支撑体系要均衡发展，但是由于贡献度不一样也不能吃大锅饭的理念。也可依此设计出简化的企业安全生产平台支撑体系评价模型。
3.关键安全特征因子评价数学模型
（1）评价模式与数学模型
对于指标的评价主要采取专家打分的方法采集，分值选择上有5分制、10分制和100分制，本书采用100分制。为了减少打分的主观性，在评价专家选择方面也有严格的要求。从数量上讲，5～7人比较符合基层的实际，当然如果条件允许，专家数量也可以适当多一些。从专家素质要求上讲，所选专家必须相对公正、客观，且是厂矿安全领域的专家。专家在打分时可以采取“背靠背”或者“面对面”的方式进行。
获得数据以后，必须对这些数据进行处理才能得到科学的评价结果。评价数学模型的选择对结果具有直接影响，主要模型有加权评分模型、一票赞成制模型、一票否决制模型。本书采用加权评分模型。专家分别对9个关键安全特征指标进行打分，然后加权计算。
根据筛选的安全特征指标体系，构造通用安全评价模型为
式中：
——平均加权评分和；
n——专家数；
Wj——第j个安全特征的权重；
xij——第i个专家对第j个特征的评分值；
s——关键安全特征指标数。
评分等级分为高度安全、非常安全、安全、值得关注、危险、非常危险、极度危险7个等级，其数值区间分别为高度安全[90，100]，非常安全[80，90），安全[70，80），值得关注[60，70），危险[50，60），非常危险[40，50），极度危险[0，40）。
（2）确定指标权重
由于选择的数学模型是加权评分模型，所以必须确定关键胜任特征指标的权重，方法是9个指标的灰关联度值分别除以它们灰关联度值的和，得到此指标的相对重要性，即为此指标的权重，用公式表达即为
通过计算，各安全特征指标权重值如表8-6所示。
表8-6 关键安全特征指标权重分配
4.应用举例
根据确定的企业安全评价模型，2011年1月对重庆10家石油生产企业进行评价，共有6位专家（分别用Z1，Z2，…，Z6表示）进行打分，则依据式（8-14）得到计算模型为
其中某油气生产企业的专家打分统计计算情况如表8-7所示。
表8-7 专家打分统计（某油气生产企业）
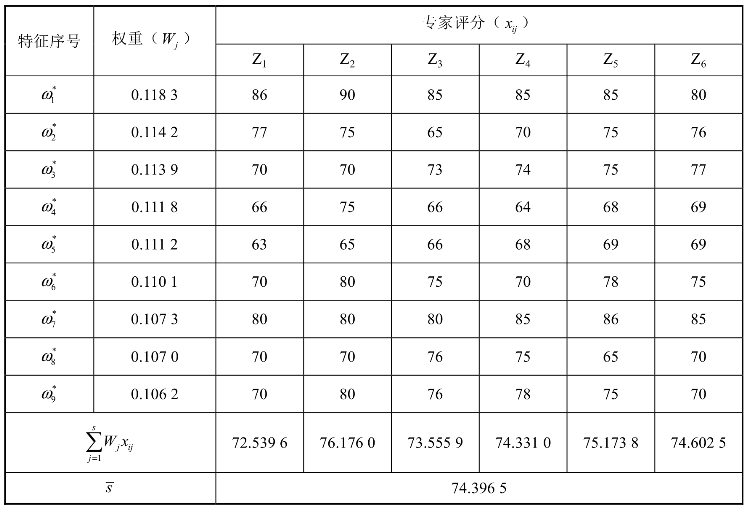
其最终分数约为74分，等级评定为安全，同理可以对其他生产企业进行评价。经过实际验证，这些安全特征指标能够比较好地评价企业安全绩效，同时具有很好的实际操作性。
- 详细阅读
-
综合物元评估方法：安全平台支撑体系宏观评价模详细阅读
对于企业安全平台支撑体系评价，我们可以采取综合物元评估方法进行粗略的评估。建立经典域如下：采用德尔菲法确定企业安全支撑体系的节域物元矩阵量值建立待评对象物元矩阵为计算得到同理可得设根据指标体系的权重分别为因为K3=MaxKi，所以该企业安全支撑体系综合评价等级为一般，需要加强投入进行安全支撑体系建设。......
2023-06-28
-
了解教师认识并评估教学活动的关键方法详细阅读
访谈法属于质性的研究方法，是通过访谈的方式了解教师对教育教学活动的认识，从而进行评估的一种方法。比起观察法，访谈可以了解受访者的思想、情绪反应，且有更大灵活性；比起问卷法，可以随时追问在访谈过程中不清楚的地方。因此访谈法可以单独使用，也可以作为观察法和问卷法的补充。与访谈者建立良好的关系是访谈成功的重要前提。......
2023-07-30
-
全局评估因子 - 如何度量成功？详细阅读
为了衡量服务提供的选择合理性，我们将α定义为考虑所有多个层次参数的全局评估因子。整体BBU功能表示为公式（9-1），其中φ是存储和CPU使用之间可调整的比例。在BBU功能中，由于尺寸不同，很难评估CPU和RAM的利用率。因此全局评估因子α符合公式（9-4），其中b和c是BBU、光网络和无线参数之间的可调整权重。这是因为BBU资源与其他资源相比变得相对足够，因此相应的权重不可避免地成为次要考虑因素。......
2023-06-19
-
数据筛选方法：按颜色、取消筛选详细阅读
若单击“按颜色筛选”项：展开列表，从中可按单元格颜色或按字体颜色对数据进行筛选，如图7-17所示。如果想取消对数据列表中某一列进行的筛选：单击该列的字段名右端的向下箭头，再选中“全选”复选框，然后单击“确定”按钮。如果想取消对数据列表中所有列进行的筛选：单击“数据”选项卡“排序和筛选”组的“清除”按钮。......
2023-11-23
-
食品安全风险监测评估方法详细阅读
《食品安全法》规定，国家建立食品安全风险监测制度，对食源性疾病、食品污染以及食品中的有害因素进行监测。食品安全风险评估结果是制定、修订食品安全标准和实施食品安全监督管理的科学依据。......
2023-08-05
-
高效设计出版企业关键绩效指标的方法详细阅读
关键绩效指标的权重是考评主体考评意图和价值观的体现，是绩效考评的指挥棒。对关键绩效指标进行审核主要是为了确保关键绩效指标能够全面、客观地反映考评客体的实际绩效，而且易于考评操作。......
2023-08-04
-
移动支付安全与隐私成为电商企业生存的关键详细阅读
根据Walker Sands Communications的调查，安全和隐私是阻碍消费者使用移动支付的最主要原因。众所周知，2020年的新冠疫情造成了不少电商企业生存状况呈现以“冰火两重天”的态势。据联商网零售研究中心不完全统计，2020年有24家具有一定规模的电商企业倒闭、调整和转型。值得注意的是，疫情因素也只是企业倒下的催化剂，大多数企业多是因为自身经营不善，缺乏核心竞争力被行业所淘汰。......
2023-11-22
相关推荐