农户社会资本指数解析

2023-06-28 理论教育版权反馈

【摘要】：3.1.2.2因子分析方法说明参考马九杰在《社会资本与农户经济》一书中关于社会资本指标构建方法，本书使用因子分析法来构建农户社会资本指数。

3.1.2.1　内部一致性分析

在进行实证分析前，先对问卷的信度和效度进行检验。信度分析（Reliability Analysis）是测度评价指标体系稳定性和可靠性的分析方法。克朗巴哈α系数是观察一组问题在同一时间组成量表题项的内在一致性如何常用的检测方法，其公式是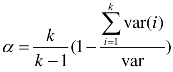 pagenumber_ebook=53,pagenumber_book=41 ，其中k 为量表评估的全部指标数，var（）i为第i个指标得分方差，var为所有指标得分的方差。信度指标可以用其量化值信度系数来考察。

一般认为信度系数好的问卷最好在0.8以上，0.5-0.8是可以接受的；如果低于0.5就应考虑修正问卷。

3.1.2.2　因子分析方法说明

参考马九杰（2008）在《社会资本与农户经济》一书中关于社会资本指标构建方法，本书使用因子分析法来构建农户社会资本指数。因子分析法是从研究变量内部相关的依赖关系出发，使用少数几个因子反映大部分指标信息的一种统计学分析方法。它的基本思想是将观测变量进行分类，将联系比较紧密的分在同一类中，而不同类变量之间的相关性则较低，那么每一类变量实际上就代表了一个基本结构，即公共因子。试图用最少个数公共因子的线性函数与特殊因子之和来描述原来观测的每一分量。因子分析法能够将事物的本质从复杂的变量中抽离出来。因子分析法的具体步骤如下：

（1）将原始数据标准化处理

在统计分析中，由于研究中所选取的指标单位可能不同导致无法进行综合性评价或者分析。原始数据进行标准化处理可以避免由于量纲不一致产生的估计差异，保证数据间是可以比较的。本书采用阀值法对指标体系进行处理。阀值法是无量纲化方法的一种，其具体公式是：

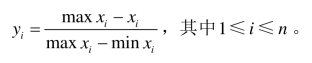
pagenumber_ebook=53,pagenumber_book=41

（2）构造因子分析模型

设有n个原始变量，表示为x1，x2，…，xn，将一系列变量进行标准化处理，使其满足均值为1，标准差为0的条件。假设n个变量可以表示为由k个因子组成f1，f2，…fk 的线性组合。因子分析主要是在分析变量的相关系数矩阵的内部结构基础上，寻找控制变量的因子f1，f2，…fk，以最大程度反映原始信息为原则选取公共因子，并建立因子分析模型。其基本公式为：

x1=a11f1+a12f2+…+a1kfk+ε1

x2=a21f1+a22f2+…+a2kfk+ε2

……

xn=an1f1+an2f2+…+ankfk+εn

利用矩阵形式可表示为X=AF+ε。其中X为可观测的n维变量矢量；F为不可测变量，每一个分量表示一个因子，也称为公共因子；矩阵A为因子载荷矩阵，其元素ank是因子载荷，指的是第n个评价指标与第k个因子间的关系，载荷越大，说明关系越密切，载荷越小，说明关系越疏远；ε是无法用因子说明的其他部分的特殊因子，服从于标准正态分布。

（3）选取因子变量

本书拣选公共因子变量的原则是特征值大于1，因子的累计方差贡献率为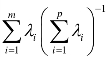 pagenumber_ebook=54,pagenumber_book=42 ，并由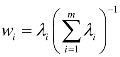确定权重值。方差贡献率是测度公共因子重要程度的指标，方差贡献率越大，表明该公共因子相对越重要，或者说方差越大，表明公共因子对变量的贡献越大。其中前m个因子包含的数据信息总量（即其累积贡献率）不低于90%时，可取前m个因子来反映原评价指标。

（4）测算综合因子得分

根据各公共因子的得分和权重，可以得到第i个样本的综合评价值：θi=∑wiFi，即第i个样本的社会资本及不同指数的量化值。

3.1.2.3　数据来源

为了保障数据的真实性和可靠性，作者于2011年4月至6月和2012年3月至5月带领由西北农林科技大学研究生院的10名研究生组成的调研团队，在陕西省咸阳市三原县做了关于小型水利设施建设、社会资本等的调查问卷和访谈调研。本次调研使用随机抽样的方法，随机选取新兴镇、渠岸乡、高渠乡、徐木乡、嵯峨乡5个乡镇，在每个乡镇中选取8个村，在每个村中选取25户农户，共1000户农户进行入户调查。采用入户调查的方式，与农户进行当面交流，然后填写问卷。每份问卷大概需要两个小时完成。本次调查活动共回收问卷1000份，有效的问卷为890份，问卷有效率为89%。

3.1.2.4　农户社会资本指数构建

本研究通过对农户社会资本的界定，选取社会网络、社会信任、社会参与和社会声望四个维度，各维度中又分别包含不同的变量，共34个变量进行指标构建。首先构建社会资本指数数理模型；然后对问卷的内部一致性进行检验，以确定量表的信度和效度；接着利用STATA12.0对不同维度的变量进行KMO检验和Anti检验，判断是否适合进行因子分析方法。一般情况下，KMO值大于0.6就说明适合因子分析，且因子分析的结果是可以接受的。最后通过计算各维度的得分，构建农户社会资本指数。

（1）农户社会资本指数的综合表达式

利用本书对农户社会资本的定义，综合考虑农村人口的特征，从社会网络、社会信任、社会声望和社会参与四个维度度量农村社会资本，其综合表达式为：

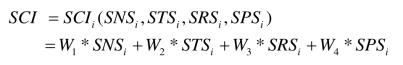
pagenumber_ebook=55,pagenumber_book=43

其中，SCIi（social capital index）表示农户i的社会资本指数，SNSi为第i个农户的社会网络得分，STSi为第i个农户的社会信任得分，SRSi为第i个农户的社会声望得分，SPSi为第i个农户的社会参与得分，用Wi（i=1，2，3，4）表示各维度的权重。

（2）一致性检验

表3-2　一致性结果

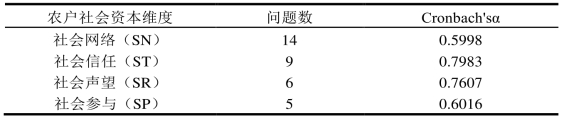
pagenumber_ebook=56,pagenumber_book=44

由表3-2可知，不同维度问题的克朗巴哈α系数（Cronbach’s α）均在0.5以上，通过了一致性检验，说明本问卷的调查指标是合适的，具有一定的合理性和参考意义。

（3）农户社会资本不同维度的指数计算

本研究利用调查数据，采用因子分析法对不同维度的细化指标赋权重，根据权重计算各维度的得分。

①社会网络

对社会网络不同变量进行KMO检验，得到结果为0.5998，且通过Anti检验，因此，数据适合进行探索性因子分析。结果如表3-3所示：

表3-3　全方差解释

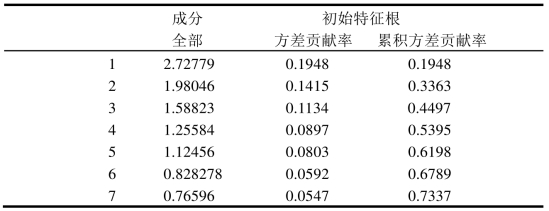
pagenumber_ebook=56,pagenumber_book=44

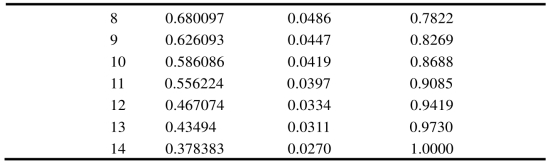
pagenumber_ebook=57,pagenumber_book=45

本研究以每个因子的方差贡献率占所选因子总方差贡献率的比重作为权重加权汇总，选取解释率为90%的前10个公共因子，用SN-i代表第i个因子，得出“社会网络”得分（SNS）：

SNS=(0.1948×SN-1+0.1415×SN-2+0.1134×SN-3+0.0897×SN-4+0.0803×SN-5+0.0592×SN-6+0.0547×SN-7+0.0486×SN-8+0.0447×SN-9+0.0419×SN-10)/0.8688

②社会信任

对社会信任9个变量进行KMO检验，结果为0.7983，且通过Anti检验，适合进行探索性因子分析。具体结果如表3-4所示：

表3-4　全方差解释

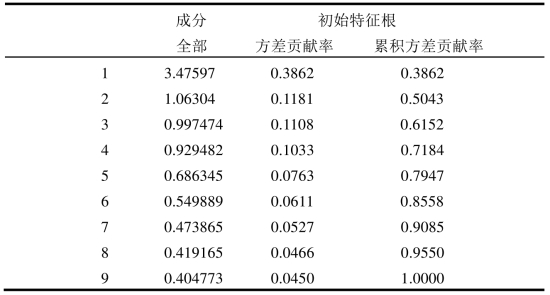
pagenumber_ebook=57,pagenumber_book=45

以每个因子的方差贡献率占所选因子总方差贡献率的比重作为权重进行加权汇总，选取累计方差贡献率大于90%的前6个公共因子，其中，ST-i代表的是第i个因子，得出“社会信任”得分（STS）：

STS=(0.3862×ST-1+0.1181×ST-2+0.1108×ST-3+0.1033×ST-4+0.0763×ST-5+0.0611×ST-6)/0.8558

③社会声望

社会声望共有6个变量，进行KMO检验的结果是0.7607，且通过Anti检验，适合进行探索性因子分析。具体结果如表3-5所示：

表3-5　全方差解释

pagenumber_ebook=58,pagenumber_book=46

以每个因子的方差贡献率占所选因子总方差贡献率的比重作为权重进行加权汇总，选取累计方差贡献率大于90%的前4个公共因子，其中，SR-i代表的是第i个因子，得出“社会声望”得分（SRS）：

SRS=(0.4566×SR-1+0.1662×SR-2+0.1271×SR-3+0.1100×SR-4)/0.8599

④社会参与

对社会参与5个变量进行KMO检验，结果为0.6016，且通过Anti检验，适合进行探索性因子分析。具体解释如表3-6所示：

表3-6　全方差解释

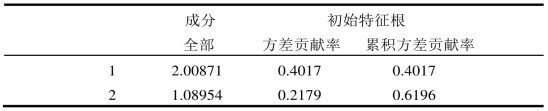
pagenumber_ebook=58,pagenumber_book=46

pagenumber_ebook=59,pagenumber_book=47

以每个因子的方差贡献率占所选因子总方差贡献率的比重作为权重进行加权汇总，选取累计方差贡献率大于90%的前3个公共因子，其中，SP-i代表的是第i个因子，计算“社会参与”得分（SPS）：

SPS=(0.4017×SP-1+0.2179×SP-2+0.1707×SP-3)/0.7904

最终根据不同维度的社会资本得分，得到各个维度的权重，农户社会资本指数的综合表达式为：

SCIi=0.36×SNSi+0.14×STSi+0.27×SRSi+0.23×SPSi

可见，社会网络在社会资本中的权重最高，为0.36，这说明社会网络对社会资本培育起到最重要的作用。社会声望和社会参与的权重相当，分别为0.27、0.23，表明社会声望和社会参与是影响农户社会资本的重要方面。社会信任在社会资本中的权重最小，为0.14，其原因可能是当前社会存在居民户信任普遍缺失的状况，农户对其他人的信任程度不高。

农户社会资本指数解析

相关推荐