地裂缝的形成原因复杂多样。地壳活动、水的作用和部分人类活动是导致地面开裂的主要原因。各种地震引起地面的强烈震动，均可产生这类裂缝。我国地裂缝灾害分布特征。仅河北、河南、陕西、山西、山东、江苏、安徽七省的不完全统计，已有200个县（市）发现地裂缝点746处。在我国发育的各类地裂缝中，除地震裂缝外，以基底断裂活动裂缝的规模和危害最大。地面沉陷裂缝多呈环状产生，各类矿区、岩溶塌陷区和地面沉降区等均有发育。......
2023-11-04
裂缝水压分布理论计算式优化
【摘要】：图4.1裂缝形状与断面流速分布如图4.1所示，裂缝中的断面流速分布为式中：ux，y为任意时刻任一点流体的流速；u0为研究断面最大流速；wx为x断面处裂缝宽度。为此，李宗利等推导得到了裂隙缝内的水压力计算公式。图4.2和图4.2为缝内水压力随时间变化在缝内不同位置的分布图。
1.基本假定
基本假定如下：①水的体积是不可压缩的；②水流属于牛顿流体，满足摩擦定律；③裂缝壁渗透系数很小，流体滤失量可以忽略；④水流在裂隙内的运动属于一维层流，任一断面任意时刻流速分布符合泊肃叶流动；⑤裂缝在某一个方向宽度远大于其他两个方向，在该方向取单位宽度简化为平面问题研究时该平面内裂缝形状为半椭圆形。
如图4.1（a）所示，在任意时刻裂缝形状的方程为
式中：a、b分别为任意时刻椭圆的长轴和短轴，是关于时间t的函数。
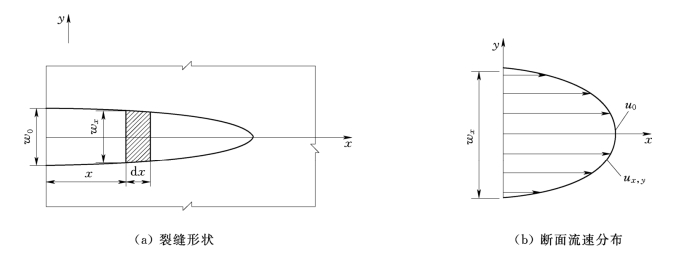
图4.1 裂缝形状与断面流速分布
如图4.1（b）所示，裂缝中的断面流速分布为
式中：ux，y为任意时刻任一点流体的流速（省略下标t，以下同）；u0为研究断面最大流速；wx为x断面处裂缝宽度。
2.质量守恒
式（4.1）右侧第一项为控制体质量随时间的变化率，对于不可压缩液体则为体积变化率，第二项为控制体周围各面流出和流入的水的通量。
取x处一微段dx如图4.1（a）所示，位于断面处裂缝宽度为wx、任一点流速为u1x，y、平均流速为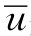
1、最大流速为u01、通过流量为qx；位于x+dx断面处裂缝宽度为
、任一点流速为u2x，y、平均流速u2、最大流速为u02、通过流量为
。
当按平面问题考虑时，微段dx的体积为
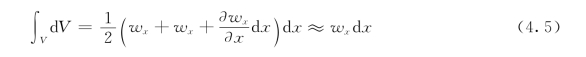
对于一维层流
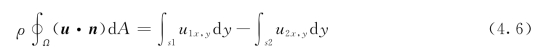
将式（4.4）代入式（4.6），并沿裂缝高度积分得
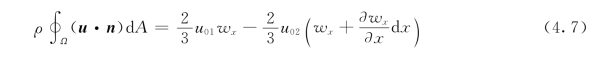
对于层流，断面最大流速等于全断面平均流速的2倍，即有
；而
，将这些关系式代入式（4.7），略去高阶微量后，得
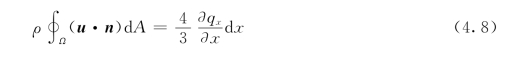
将式（4.5）和式（4.8）代入式（4.1）得到裂缝水流量与裂缝宽度变化的关系如下
3.缝内压力公式
任一断面裂缝的张开宽度为
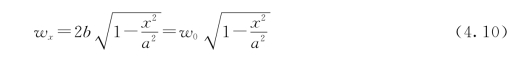
式中：w0为裂缝边缘的张开宽度。
大量研究表明，岩石与混凝土等脆性材料裂纹断裂失稳扩展具有跳跃性，裂缝长度并不是持续向前扩展，而是扩展到某一稳定状态即停止，待断裂能积聚到一定程度后再出现一次跳跃。为此，李宗利等推导得到了裂隙缝内的水压力计算公式。
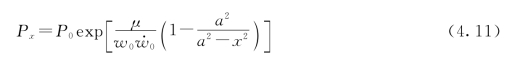
式中：μ为水的动力黏滞系数。
由于
，由指数函数的性质知裂缝内水压沿裂缝长度按指数规律减小，随裂缝边缘张开宽度及张开速率的增大，式（4.11）中的指数部分减小，缝内水压增大。而
，说明随着时间的推移，缝内水压力逐渐增大。图4.2（a）和图4.2（b）为缝内水压力随时间变化在缝内不同位置的分布图。
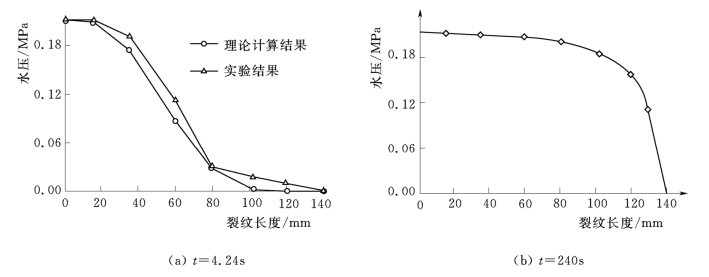
图4.2 裂缝内水压分布
有关工程渗流理论研究与实践的文章
- 详细阅读
-
多相流耦合理论研究：储层裂缝建模详细阅读
由以上方程知，双孔单渗模型基本控制方程组有S wm，S om，S wf，S of，Pw m，Pom ，Pw f，Pof共8个未知量，方程组的数目也是8个。Pcowm，Pcowf，Krwm，Krom，K rwf和K rof则由两相流实验得到。......
2023-08-20
-
联肢剪力墙的裂缝分布和破坏形态分析详细阅读
在水平荷载作用下，联肢剪力墙的墙肢可能出现弯曲破坏或剪切破坏，墙肢的内力分布和破坏形态与连梁刚度和连梁承载力有密切关系。另一种情况是联肢剪力墙中受压墙肢的剪坏，美国伯克利加州大学所作的双肢剪力墙就出现了这种破坏，原因是在塑性变形的过程种受压墙肢的剪力增大，设计时对其估计不足而使墙肢受剪承载力不够，造成墙肢剪压破坏[61]。......
2023-08-23
-
博弈论与三十六计：理论预设比较详细阅读
毫无疑问，经典博弈论与三十六计都是存在理论预设的，三十六计比起经典博弈论来与现实生活的距离要更近一些，就是说更贴近社会生活的真实状况。[2]理论预设是理论建构的重要基础，经典博弈论和三十六计各自的理论预设决定了它们的理论建构是非常不同的。......
2023-12-02
-
储层裂缝建模与多相流耦合理论研究的成果详细阅读
本小节基于基本的牛顿力学对储层平行平面裂缝流进行分析。在图中流体微元主要受到压力差和剪切力的作用，其中压力差取决于裂缝两端的水头压力差值，而剪切力则取决于裂缝中流体的流速分布。进一步分析，储层裂缝中流体在裂缝上壁面的剪切应力为：由于裂缝高度非常小，所以该剪切应力对储层固体骨架的剪切作用也非常小。......
2023-08-20
-
储层裂缝建模与多相流耦合理论的研究成果详细阅读
由以上方程可知，整个双孔双渗模型基本控制方程组共包含S wm，S om，S wf，S of，Pw m，Pom，Pw f，Pof 共8个未知量，方程组的数目也是8个。Pcowm，Pcowf，Krwm，Krom，则由两相流实验得到。......
2023-08-20
-
裂缝走向对渗流的影响：多相流耦合理论研究详细阅读
由于要分析裂缝走向对渗流的影响，本次模拟在保持井排方向不变的情况下，设计了4种不同裂缝走向的储层进行模拟计算。这是由于双重介质中裂缝系统渗透率的各向异性导致的。图104 P1井累计产水量变化图图105 P2井日产油量变化图图106 P2井累计产水量变化图图107-图109给出了井排方向与裂缝走向4种相对关系下的P3井日产油量、P3井累计产水量及油藏平均地层压力变化。......
2023-08-20
-
储层裂缝建模与多相流耦合理论研究成果详细阅读
无网格扩展有限元方法的工作原理是允许网格在不进行重新劈分的情况下模拟网格单元中的不连续面。无网格扩展有限元方法就是基于这一点，在传统有限元方法的基础上引入非连续性函数表示裂缝处的非连续位移。在非各向同性的储层岩石介质中，裂缝尖端奇性场依赖于裂缝尖端的具体位置，因此要准确地模拟裂缝尖端奇性场，需要不断追踪裂缝的扩展轨迹，降低模拟速度。一种替代方案是基于裂缝扩展沿断裂径迹扩展行为的扩展有限元模拟方法。......
2023-08-20
相关推荐