如图1-13所示，液体在一直径为d的圆管内做层流运动，即Re＜Rexp=2320。图1-13 圆管中的层流在液流中取一小圆柱体，小圆柱体的直径为2y，长度为l，并设液流从左向右流动。......
2025-09-29
层流状态下的渗透系数计算公式
【摘要】：当压水试验过程中设置渗压计观测孔时，可以利用压水水流达到稳定状态下观测孔内的孔隙水压力和压水孔内的水压力关系来计算岩体的渗透系数。因此，当测压孔渗压计读数较小时，可以应用压水试验规程建议的渗透系数公式估计岩体的高压渗透系数。
当压水试验得到的透水率较小（＜10Lu），且P-Q流量关系曲线类型为层流时，压水试验规程建议岩体的渗透系数计算公式为
式中：K为岩体的渗透系数，cm/s；Q为压入流量，cm3/s；H为试验水头，cm；L为试验长度，cm；r为钻孔半径，cm。
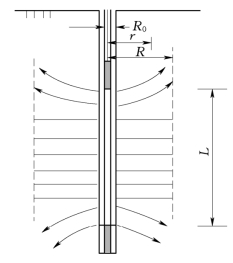
图3.1 试验孔周岩体内水流示意图
在我国，大部分工程进行高压压水试验时都不在压水孔附近岩体中设置渗压计来记录岩体中的水压力随压水孔压力的变化过程。因此，岩体的渗透性只能通过分析压水试验孔中的流量与压力关系曲线来确定。
当压水试验过程中设置渗压计观测孔时，可以利用压水水流达到稳定状态下观测孔内的孔隙水压力和压水孔内的水压力关系来计算岩体的渗透系数。假定裂隙岩体为各向同性岩体，试验过程中裂隙岩体中的水流近似为径向流，见图3.1。当压水过程中试验流量与压力达到相对稳定情况下，任意过水断面上（半径为r的圆柱面）的总流量均相等，即
根据达西定律有
取Lr=LR，于是，
。(https://www.chuimin.cn)
距离钻孔r处的水头（压力）增量为
通过距离钻孔R处的断面的流量为
将式（3.4）代入式（3.5）并整理得渗透系数计算公式
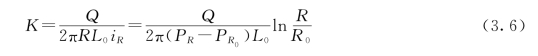
式中：K为岩体的渗透系数，cm/s；Q为压入流量，cm3/s；PR和PR0分别为测压孔与压水试验孔孔内的总水头，cm；L0为试验长度，cm；R0为钻孔半径，cm；R为测压孔与压水试验孔之间的距离，cm。
式（3.6）与《水利水电工程钻孔压水试验规程》（SL 31—2003）建议的计算公式在形式上一致，其不同之处如下：
（1）式（3.6）的对数项分子取测压孔与压水试验孔中心距离R，规程建议的式（3.1）中对数项分子取试验段长度L。
（2）式（3.6）中的分母项采用的是测压孔与压水试验孔之间的水头差，而规程建议的式（3.1）中采用压水试验孔中的水头值。
如果假定压水试验中距离压水孔L处的孔隙水压力衰减为零，此时式（3.6）与压水试验规程建议式（3.1）完全相同。因此，当测压孔渗压计读数较小时，可以应用压水试验规程建议的渗透系数公式估计岩体的高压渗透系数。
相关文章
- 详细阅读
-
层流、湍流和雷诺数的基本概念详细阅读
雷诺数是用来表征流体流动情况的无量纲数，以Re表示。雷诺数大，意味着惯性力占主要地位，流体呈湍流流动状态。对于管内流动雷诺数Re<2300为层流状态，Re＞4000为湍流状态，Re=2000～4000为过渡状态。上式表明，雷诺数可理解为在流体运动中惯性力对粘性力的比值。层流时的速度分布呈抛物线状，从图3-3中可发现，因此对于层流流体，只要知道中心速度Vmax，就可推算出平均速度和流量。图3-3 层流和湍流的速度分布图3-3 层流和湍流的速度分布......
2025-09-29
-
坡面产沙计算公式详解详细阅读
图6-9坡面侵蚀单元设泥沙颗粒顺坡的平均运动速度为vs，则单位时间内单位宽度坡面上通过观察面流出的泥沙所占面积为vs，即图中阴影部分的面积。将此关系代入式得到在较小尺度的坡面上，由于降雨近似均匀，单宽流量q 与单位面积上的径流量qe存在关系:q=qex，其中x 为沿坡面向下的坐标。由于坡面概化为矩形斜坡，设坡面面积为A，坡长为L，则坡面的宽度B=A/L。......
2025-09-29
-
弹性接触应力的计算公式与基本参数详细阅读
由Hertz推导出的弹性变形和接触应力计算基本公式为式中 a、b——接触椭圆长、短半轴；σmax——最大接触应力；δ——弹性趋近量；μ、ν——与曲率函数F（ρ）有关的椭圆积分，列于表2-2中；E、——材料的弹性模量和泊松比；Q——使两接触体压紧的法向载荷，在滚动轴承中为滚动体载荷；∑ρ——接触处主曲率之和。但表2-4和上述系数的计算前提是两接触体均用钢材制造。 计算7208C轴承中的最大接触应力σmax与a、b、δ。......
2025-09-29
-
掌握杆杠原理：力与位移计算公式及杠杆类型详解详细阅读
杠杆就是一个简单的梁，能够铰接在旋转关节或者杠杆支点上。力与位移的计算公式如下：力（L÷X）×FA=FG位移（X÷L）×MA=MG图1-3二级杠杆图1-4三级杠杆图1-4所示为一个三级杠杆。三级杠杆与二级杠杆的不同之处在于施力点的位置以及作用力的方向。在这类杠杆中，施力点位于杠杆支点和力产生点之间。图1-5杠杆与边杆直角杠杆的角度是90°，属于一级杠杆，其最典型的应用是在连杆系统中改变施力的方向。......
2025-09-29
-
三种不同的服装结构形式：技术的、肖像的和文字详细阅读
在巴特看来，时尚是一个由图像服装、书写服装和真实服装构成的系统。于是和其他所有的物体一样，巴特将这三种不同的服装结构形式归纳为：技术的、肖像的和文字上的。巴特还将图像服装和书写服装分别称为“图像展示的服装”和“文字描述的服装”，并将两者统称为“虚拟的服装”。......
2025-09-29
-
基于模板匹配的检索方法的介绍详细阅读
这一模型意味着在我们的知识基础中，已经存储了数以百万计的不同模板——每一个可以辨识的不同物体或模式，都有一个与之匹配的模板存在。本书结合局部特征的特点和模板匹配的原理，提出了一种图像检索方法。如果局部特征和模板匹配的数量越多，则该幅图像和查询图相似的程度就越高。显然，模板匹配并不完全适合知觉原理的实际应用。......
2025-09-29
-
契铁块的绘制的分析介绍，详细阅读
任务描述在Pro/E 5.0的草绘类别中使用直线命令，绘制如图1-1-1所示契铁块的二维视图，并以“1-1-1”为文件名命名保存。图1-1-1契铁块任务实施一、Pro/E 5.0软件的启动图1-1-2启动图标方法1双击桌面图标，即图1-1-2所示“proeWildfire 5.0.exe”快捷方式图标。步骤1绘制第一条水平线。图1-1-17文件保存图1-1-18保存对象以上就是图1-1-1的整个绘制操作方法。......
2025-09-29
相关推荐