首页理论教育渗流微分方程：热流固非饱和渗流控制方程中的第二组方程

渗流微分方程：热流固非饱和渗流控制方程中的第二组方程

2025-09-29 理论教育版权反馈

【摘要】：式中相关导数关系为4.渗流微分方程为建立水相和空气的渗流微分方程，将渗流本构方程和状态方程代入连续方程，并略去较小量pg/t项，整理得这就是热流固非饱和渗流控制方程中的第二组方程。

渗流微分方程由连续方程、达西定律、菲克定律和状态方程联立求出。

1.连续方程

非饱和多孔介质三相（水、气体、固体）连续方程分别为

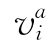式中：ρfw、ρfa、ρv、ρa和ρs分别为液相中的水和溶解空气的密度、气相中的水蒸气和空气的密度以及固体密度；分别为水、气相中的水蒸气、气相中的空气和固体颗粒的速度，对非饱和带， pagenumber_ebook=54,pagenumber_book=43 =0；qmw和qma分别为水和空气质量源（汇）强度，由于平衡条件下蒸发和液化的质量总相等，所以互相抵消，即qmw=0和qma=0。

上述速度均指相对于固定坐标系而言，引入液相和蒸汽相对于固体的相对速度vrf和vrv，即vrf=vf-vs，vrv=vv-vs

将上述表达式代入连续方程，展开得

将式（2.102）乘以（sρfw+ρvsg）/ρs，然后与式（2.100）相加，消去∂φ/∂t，得到孔隙介质中水的连续性方程为

孔隙介质中气体连续性方程为

式（2.103）和式（2.104）就是非饱和孔隙介质中的两个流体连续方程。

2.达西定律和菲克定律

连续性方程中包含4个速度项，为了使渗流方程中只出现p、T、s和ui4个未知量，需要对这些速度项进行处理。对于非饱和带中的空气，认为。液体相对速度和蒸汽相对速度分别用达西定律和菲克定律表示。固体速度项的散度可用位移分量的导数表示。据达西定律有

据菲克定律有

式中：κrw为气水两相流中水的相对渗透率；Dv为蒸汽在空气中的扩散系数；μw为温度相关的黏滞系数。(https://www.chuimin.cn)

3.状态方程及相关导数

连续性方程中，不同物质的密度与孔隙压力、温度以及饱和度相关。各种密度的状态方程为

其中R=8314J/（kmol·K）、Rv（R/Mv）=641.5J/（kg·K），Ra=287J/（kg·K）

式中：βw、βfa、βTm、βMm分别为液相水、溶解孔隙的体积热膨胀系数、固体基质的热膨胀系数和湿胀系数；R、Rv（R/Mv）、Ra分别为普适气体常数、水蒸气的气体常数和空气的气体常数；Mv为蒸汽的分子量，kg/kmol；RH为相对湿度；ρvs为饱和水蒸气密度。

溶解空气的压缩系数cfa可以认为与液体水的压缩系数cw相等，溶解空气的热膨胀系数βfa可以认为与水的热膨胀系数βw相等。

另外，上述变量之间还存在以下关系

式中：pc为毛细管压力。

式（2.107）中相关导数关系为

4.渗流微分方程

为建立水相和空气的渗流微分方程，将渗流本构方程和状态方程代入连续方程，并略去较小量∂pg/∂t项，整理得

这就是热流固非饱和渗流控制方程中的第二组方程。其中系数定义为