控制方程求解的方法与优化

2023-06-28 理论教育版权反馈

【摘要】：式即为动态分析中实际求解的有限元代数方程组。由于式考虑了渗透张量与应力的耦合关系，即使采用弹性本构模型，式也是一个非线性方程组，仍需在每一个计算时步内迭代求解。当然与式相比，式消除了自由面边界非线性的影响，非线性仅来源于随应力的变化，非线性程度减弱了，因此数值分析的计算量也减小了，收敛性也可以保证。

渗流场和应力场全耦合的过程是一个动态的过程，其求解需借助有限元等数值方法完成。为实现耦合过程中渗流场和应力场之间的相互耦合，可采用间接耦合法和直接耦合法。直接耦合法是在求解流固耦合控制方程式（2.57）和式（2.58）过程中将未知变量位移和孔隙压力纳入同一组方程中，在求解位移方程中直接增加渗流引起的节点不平衡力增量，而在求解节点孔隙压力方程中增加节点位移改变引起的节点流量增量。

1.空间域离散

考虑到动态耦合问题具有时间分段计算、荷载逐级施加以及自由面迭代的非线性等特性，需建立增量形式的有限元分析格式。假定在某级荷载增量下，产生的位移增量为Δu，增量形式的位移计算有限元方程控制方程组为

式中：Δp为未知孔隙水压力增量列阵；Δp*为已知节点孔隙水压力增量；G′为单元位移自由度选择矩阵；B′为应变矩阵：L={1，1，1，0，0，0}T；N={N1，N2，…，Ni，…，N8}；N′为节点位移形函数矩阵；分别为单元已知边界面力和体积力增量列阵，一般情况下有[Δf]e={0，0，-Δγ}T；ΔFn为已知节点集中力列阵。

耦合分析的渗流控制方程组为

式中：u、p分别为未知节点位移和孔隙水压力列阵；pe*为第一类渗流边界节点已知水压力列阵；qe为单元已知边界法向流量；G为单元孔隙水压力自由度选择矩阵；ke为单元渗透系数张量，且ke=[kij]，是应力张量的函数。

需要指出的是，K″、Q0两项是与自由面相关的，对于承压流而言，此两项不存在；但对于无压渗流，对自由面边界单元需要计算K″，此项对内部单元而言为0。

2.时间域离散

连续性方程进行空间离散后所得式（2.60）包含了节点位移、孔隙水压力对时间的微分项，因此，需要将式（2.60）在时间域内进一步离散。不妨取动态计算时间步长为Δt，引入时间因子α，式（2.60）可改写为

式中： pagenumber_ebook=46,pagenumber_book=35 为的转置矩阵。

为了使求解迭代过程稳定收敛，通常取0.5≤ξ≤1.0。假定位移、孔隙水压力在时间段t～t+Δt内呈线性变化，则有下列各式成立：

代入式（2.61）并整理可得

考虑到一般情况下，边界补给流量Q在时间段t～t+Δt内变化不大，式（2.62）可简化为

于是，式（2.63）可改写为

式（2.64）即为渗流连续性方程在时间域和空间域内离散后得到的增量形式有限元方程。

3.动态全耦合有限元方程组及迭代求解

联合式（2.59）和式（2.64），可获得饱和孔隙介质渗流场与应力场弹性动态耦合定解问题的增量形式的有限元方程组：

由于 pagenumber_ebook=47,pagenumber_book=36 为应力张量的函数，对于某一级荷载下的每一个计算时步Δt而言，当研究域内存在自由面位置，且事先不确定时，中包含的K″是随自由面位置的变动而改变的，因此，动态耦合有限元方程组（2.65）是一个强烈的非线性方程组，在每一个计算时步Δt内都需要迭代求解。

动态耦合有限元方程组（2.65）的直接迭代格式如下：

式中上标k、k+1分别为各分项在第k、k+1次迭代结束时相应的值。式（2.66）即为动态分析中实际求解的有限元代数方程组。求解过程在时间段t～t+Δt内迭代稳定之后，即可近似确定t+Δt时刻的自由面位置，并获得该时刻的位移、孔隙水压力增量；依据该时刻的应力和自由面位置重新计算系数矩阵 pagenumber_ebook=47,pagenumber_book=36 ，以迭加后的节点位移值、孔隙水压力值作为初始条件，开始下一时步的计算，直到本级荷载终了时刻为止。

该时步计算完成后，施加荷载增量，进行荷载增量步循环，直到加载结束。需要指出的是，对承压流而言，K″是不存在的，此时式（2.66）可简化为

式中：Δ pagenumber_ebook=47,pagenumber_book=36 为Δ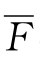中扣除初流量项之后的等效流量增量列阵。

由于式（2.67）考虑了渗透张量与应力的耦合关系，即使采用弹性本构模型，式（2.67）也是一个非线性方程组，仍需在每一个计算时步内迭代求解。当然与式（2.66）相比，式（2.67）消除了自由面边界非线性的影响，非线性仅来源于随应力的变化，非线性程度减弱了，因此数值分析的计算量也减小了，收敛性也可以保证。

控制方程求解的方法与优化

相关推荐