可是，事实上，却很少在国内发现有推广设计CAE的优秀事例。不从认识上消除这些担心，就难以在设计现场推广应用CAE，这也是没有引进设计CAE的一个原因。现在本田大量地采用了设计CAE，实现了从KKD设计到设计CAE的转变。在领导人员认识和理解了设计CAE的重要性和优越性以后，问题就成功了一半。特别要注意采用那些设计人员易于熟悉的工具，如与CAD系统集成的CAE工具。......
2025-09-29
连续性方程在直角坐标系中的应用
【摘要】：欧拉连续性方程是欧拉在1755年建立的。按欧拉方法，如图1.12所示，首先选取控制体元——固定在空间上的一个确定的、形状任意的封闭体积，位置保持不变。控制体元可以非常小，如小到前文所述的特征体元；或者有限大，这需要根据研究问题所确定。控制体元的形状不会影响所得到的方程。ρv也称质量速度，它是单位时间内通过单位面积的流体质量。
欧拉连续性方程是欧拉在2025年建立的。按欧拉方法，如图1.12所示，首先选取控制体元——固定在空间上的一个确定的、形状任意的封闭体积，位置保持不变。控制体元可以非常小，如小到前文所述的特征体元；或者有限大，这需要根据研究问题所确定。控制体元的形状不会影响所得到的方程。对于取定的控制体元，在不考虑流体的注入或渗失情形下，给定时间段内质量守恒定律的文字表达式为
图1.12 控制体元
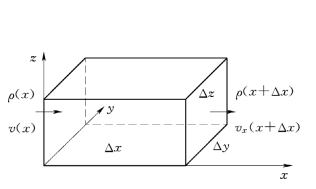
图1.13 直角坐标控制体元
在水平、均匀介质中，取一个长方体为控制单元，见图1.13，体元边长分别为Δx、Δy、Δz，不可压缩流体密度为ρ，流体在x、y、z方向上的流速（流速的投影）为vx、vy、vz。若仅存在沿x方向的流动，在Δt时间段内流体流入单元体的流体质量
流出单元体的流体质量
(https://www.chuimin.cn)
在Δt时段内单元体内流体质量增量为
对于不可压缩流体，密度不随时间变化，联立式（1.75）、式（1.76）和式（1.77），有
两边同时除以（ΔxΔyΔzΔt）再取极限，根据微分的定义可以得到一维渗流连续性方程
若考虑三维流动，结果必然有
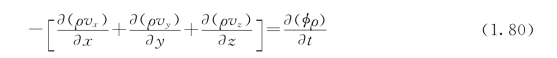
式（1.80）的左边是流体单位体积扩张速度，即流速散度。ρv也称质量速度，它是单位时间内通过单位面积的流体质量。
相关文章
- 详细阅读
-
机器视觉系统在实际应用中的作用详细阅读
若引入机器视觉取代传统的人工检测方法，能极大地提高生产效率和产品的良品率。同时，机器视觉技术还能在检测超标准烟尘及污水排放等方面发挥作用。利用机器视觉，能够及时发现机房及生产车间的火灾、烟雾等异常情况。此外，许多场合使用其他方法难以完成检测任务，机器视觉系统则可出色胜任。......
2025-09-29
-
变频器在实际应用中的作用及应用案例详细阅读
可编程序控制器、变频器、伺服电机、人机界面是驱动控制系统中不可缺少的组成部分。通常，纺织机械系统中的电动机普遍采用通用变频器控制，所有的变频器则统一由PLC控制。图解演示例如，图11-35所示变频器在电梯智能控制中的应用。图11-35 变频器在电梯智能控制中的应用5.变频器在民用改善环境中的应用随着人们对生活质量和环境的要求不断提高......
2025-09-29
-
振动在机械加工中的应用和控制详细阅读
干扰力消除，强迫振动停止。自激振动（颤振）机械加工过程中，在没有周期性外力的作用下，由系统内部激发反馈产生的周期性振动。自激振动的频率等于或接近于系统的固有频率。自激振动能否产生及其振幅的大小，决定于每一振动周期内系统所获得的能量与系统阻尼消耗的能量的对比情况。......
2025-09-29
-
梁的强度条件在实际工程中的应用详细阅读
在梁的强度计算中，必须同时满足正应力和剪应力两个强度条件。通常先按正应力强度条件设计出截面尺寸，然后按剪应力强度条件进行校核。但在以下几种情况下，需校核梁的剪应力：①最大弯矩很小而最大剪力很大的梁；②焊接或铆接的组合截面梁；③木梁，因为木材在顺纹方向的剪切强度较低，所以木梁有可能沿中性层发生剪切破坏。按强度条件求许用荷载[F]。......
2025-09-29
-
霍尔式传感器在实际应用中的作用详细阅读
则B正比于Ui，霍尔器件的Uo正比于B。此角位移测量仪可以改造为霍尔电压传感器，测量直流电压。图3-14所示为霍尔传感器测量转速方法的示意图。在铁心上开一与霍尔传感器厚度相等的气隙，将霍尔线性器件紧紧地夹在气隙中央。......
2025-09-29
-
分形理论在焊接中的应用探析详细阅读
分形理论的诞生才不过20多年，但它对多种科学产生了巨大的影响。分形理论长期以来一直被认为是对病态的、奇形怪状的、不规则的等一大类自然现象提供一种极其简洁的数学描述方法。目前，分形理论已被广泛应用于自然科学与社会科学的众多领域，在图像处理方面已经被应用于图像边缘检测、图像编码、图像压缩等领域。因此，采用分形这种非线性的图像处理算法对焊接图像进行预处理。......
2025-09-29
-
浸渍钎焊技术在实际应用中的案例分析详细阅读
为了保证焊接质量，钎焊前需要仔细清洗焊件，目的是把焊件表面的油渍及厚氧化膜去除。预热温度为500～540℃，保温2～5min。盐浴钎焊时应尽可能保证密闭通道内空气排出，防止空气被封闭在空腔内阻碍熔盐润湿所有待钎表面。氟化物钎剂在钎焊过程中依靠溶胀作用使氧化膜强度下降，同时氧化剂的存在降低了金属的表面张力使钎料易于铺展。熔盐准备过程中，要保证熔盐的pH值为5.3～7.0。如果pH值超过7.0，则需AF添加剂调节。......
2025-09-29
相关推荐