首页理论教育非线性渗流定律的研究与应用

非线性渗流定律的研究与应用

2023-06-28 理论教育版权反馈

【摘要】：当流体渗流服从达西定律时，通过某截面的流量与水力梯度成过原点的直线关系；当流量和水力梯度关系不能用直线关系表示时，这样的渗流过程就是非达西渗流过程，或称非线性渗流。由此得出结论，在Re＜5范围内达西定律是适用的。如图1.11所示，渗透性与压力关系可用下式表述此时，一维渗流情形下达西定律可写为因为流体没有密切接触固体壁面，所以低压气体分子在固体壁面上可以具有一定的非零速度。

达西定律有相应的适用条件。当流体渗流服从达西定律时，通过某截面的流量与水力梯度成过原点的直线关系；当流量和水力梯度关系不能用直线关系表示时，这样的渗流过程就是非达西渗流过程，或称非线性渗流。

1.达西流高速上限——雷诺数判断准则

1880年，雷诺.Q通过用不同的圆管做水流流态实验，发现了管中水流形态可分为层流和紊流两种流态。流态可用无量纲雷诺数来判。雷诺数定义如下，

pagenumber_ebook=28,pagenumber_book=17

式中：Re为雷诺数；d为圆管直径，m；ρ为流体密度，kg/m3；U为圆管内流体平均速度，m/s；μ为流体黏度，Pa·s。

雷诺数表示了惯性力与黏滞力之比，若惯性力占主导地位，则雷诺数大；若黏滞力占主导地位，则雷诺数小。

对于多孔介质，根据单根毛管渗流定律可得

pagenumber_ebook=28,pagenumber_book=17

孔隙介质渗流截面上的渗流速度和真实流速满足D-F关系式，即

将式（1.62）和式（1.63）代入式（1.61），得

式中：v为渗流速度，cm/s；κ为渗透率，D；μ为动力黏度，cP；ρ为流体密度，g/cm3；φ为孔隙度。

在渗流理论中，20世纪20年代巴普诺夫斯基首先提出用雷诺数作为达西定律的应用判断准则。Fancher和Lwewis（1933）利用气体通过各种可渗透的岩芯完成了大量的实验，得到了范宁摩擦系数f与雷诺数（Re）的关系曲线。根据f与Re的关系绘制出一张双对数模式图，见图1.8。

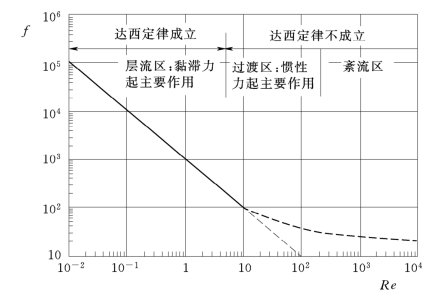
pagenumber_ebook=29,pagenumber_book=18

图1.8　孔隙介质渗流流动分类模式图

图1.8表明，多孔介质的流动可分为3个区域：层流区、过渡区和紊流区。第一区域，在Re＜5范围内是斜率为-1的直线段；第二区域，在5＜Re＜100范围内有一个二次曲线形式的过渡段；第三段则是一个水平线段。

第一区域为层流区，黏滞力起主要作用，f-Re的双对数直线特征表明有下式成立，

式中：C为回归常数。

范宁摩擦系数f的定义为

利用式（1.54a）和式（1.63），将之代入式（1.66），得

将式（1.61）和式（1.67）代入式（1.65），并利用式（1.60），可得

pagenumber_ebook=29,pagenumber_book=18

其中，d=2r0。

式（1.68）与达西定律表达相同。由此得出结论，在Re＜5范围内达西定律是适用的。

第二区域为过渡区，黏性力仍起重要作用，但逐渐减弱至惯性力起主要作用，流动先是层流，其后逐渐变为紊流，其方程为

式（1.69）与Forchheimer（1930）提出的二项式一致。另外，根据Ahmed和Sunada（1969）对多种非固结多孔介质的研究表明，在较高渗流流速下有下列关系式

pagenumber_ebook=29,pagenumber_book=18

其中，β为非达西流因子，而n与多孔介质特性有关，n的不同取值决定了指示曲线（渗流速度与压力梯度的关系曲线）的变化特征，见图1.9。

第三区域为紊流区，在Re＞100的条件下流体流动变为紊流。紊流实际上是一种混沌现象，在渗流力学中较少遇到。

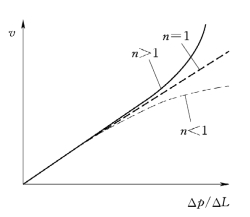
pagenumber_ebook=30,pagenumber_book=19

图1.9　高速渗透流速与压力梯度关系

2.低速下限——启动压力梯度

对于低渗透介质或非牛顿宾汉姆流体，渗流定律可写为

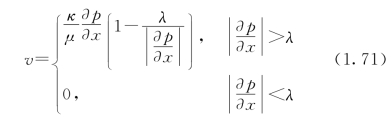
pagenumber_ebook=30,pagenumber_book=19

式中：λ为启动压力梯度，它由介质的结构特性或流体的性质所决定。

低速渗流情况下，指示曲线见图1.10。在实验室中，低速渗流常常因为速度微小而造成测量方面的困难，因此这一阶段很难准确验证。

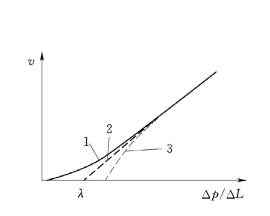
pagenumber_ebook=30,pagenumber_book=19

图1.10　低速渗透流速与压力梯度关系

1—低速非线性渗流；2—低速达西流；3—低速流

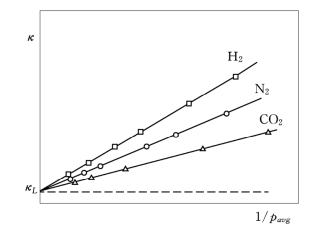
pagenumber_ebook=30,pagenumber_book=19

图1.11　流体滑脱效应

3.密度下限——滑脱效应

在气体渗流过程中，低压气体将产生Klinkenberg（1941）效应和分子扩散。用不同的气体测试同一块岩芯的渗透率，渗透率将是平均压力的函数，结果见图1.11。如图1.11所示，渗透性与压力关系可用下式表述

此时，一维渗流情形下达西定律可写为

因为流体（通常是气体）没有密切接触固体壁面，所以低压气体分子在固体壁面上可以具有一定的非零速度。因此，当气体分子的平均自由程接近于孔道尺寸时，气固界面上的各个分子都将处于运动状态，若与液体渗流相比较，此时气体渗流中便增加了一份附加通量，这正是气体滑脱的实质。

实际工程中产生的非线性过程远比这种复杂。产生非线性渗流的原因可以总结如下：

（1）渗流速度过高、流量过大。

（2）分子效应（气体滑脱）。

（3）离子效应（例如盐水在含有黏土的砂岩中渗流，实验发现渗透率随含盐度或渗流速度的增加而增加，原因是流体中的离子与多孔介质表面相互作用）。

（4）流速过低（低渗透介质）。

（5）非牛顿流体。