对于可控整流电路，只要满足一定条件便可工作于有源逆变状态，此时电路形式未作任何改变，只是工作条件发生变化。无源逆变将在后面讨论，本节只讨论有源逆变。电源间能量的流转关系在分析有源逆变电路的工作原理时，弄清电压之间能量的流转关系是非常重要的。整流与有源逆变的根本区别在于能量的传递方向不同。以上两个条件必须同时满足，直流电路才能工作在有源逆变状态。还应指出，并不是所有整流电路都可以工作在有源逆变状态。......
2023-06-23
连续介质的定义及特点分析
【摘要】：多孔介质特征体元由两部分构成，即孔隙度和连续介质。如图1.2所示，称体积ΔV0为多孔介质在数学点M处的特征体元，即多孔介质特征体元。孔隙度为连续函数时，多孔介质便成为连续多孔介质，简称连续介质。应当注意的是，连续流体和连续介质模型也是有局限性的。在这些情况下，连续介质和连续流体模型不能原封不动的套用。图1.2多孔介质孔隙度的定义
连续介质思想就是用一种假想的连续介质（无结构物质）代替实际的多相流体或多孔介质。在这种假想的连续介质中，可以把运动变量、动力参数及变量看成是空间坐标和时间的连续函数。因此，我们就能够运用高等数学来研究流体在多孔介质中的渗流运动，就能够对真实的渗流过程作出合理的分析和解释。
1.流体连续性
对于流体，可以看做是由分子集合体组成的、充满整个空间的具有连续密度函数的理想流体，称之为连续流体，简称流体。这一概念是欧拉在1755年提出的。对于任意相邻的两点P1和P2，如果流体是连续的，则必须满足下式
2.固体连续性
对于岩土体一类的多孔介质，结构之间往往存在不连续的面，因此实际上岩土体都是不连续体。为便于进行力学分析，也需要对其进行连续性的等效处理。为此，提出了多孔介质特征体元的概念。
多孔介质特征体元由两部分构成，即孔隙度和连续介质。对于多孔介质中某一点的孔隙度定义来说，首先必须选取一定的体积空间，这个体积空间不能太小，应当包括足够的有效孔隙数（连通的，可供流体通过的空间）；但该体积空间又不能太大，否则不能够代表介质的局部性质。
介质在M点孔隙度的严格定义为
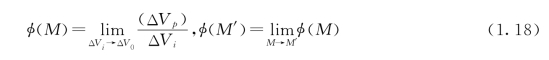
这一定义有时叫做推定极限（Hubbert，1956）。
如图1.2所示，称体积ΔV0为多孔介质在数学点M处的特征体元，即多孔介质特征体元。孔隙度为连续函数时，多孔介质便成为连续多孔介质，简称连续介质。若这样定义的孔隙度与空间位置无关，则称该介质对孔隙度而言是均匀介质，此时孔隙度可简单定义为岩块中的孔隙体积Vp占岩块总体积V的分数
孔隙度是标量，有线孔隙度、面孔隙度和体孔隙度之分，对于均匀介质是相等的。区分孔隙类型是非常重要的，一种是相互连通的有效孔隙，另一种是相对孤立的、不连通的死孔隙。在不同的场合，不同类型的孔隙对渗流过程的贡献是不同的。
应当注意的是，连续流体和连续介质模型也是有局限性的。当流速超过某一极限速度时，水流会出现掺气现象；压力小于汽化压力，会产生局部空化现象。在这些情况下，连续介质和连续流体模型不能原封不动的套用。
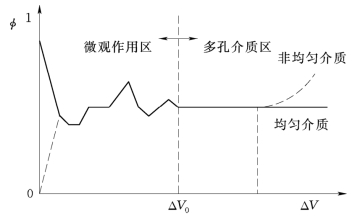
图1.2 多孔介质孔隙度的定义
有关工程渗流理论研究与实践的文章
- 详细阅读
-
公众与群众的定义及特点详细阅读
所谓公共关系的公众,是指因面临某个共同问题而形成、并与社会组织的运行发生一定联系的社会群体。或者说,公众是指与一个组织机构直接或间接相关的个人、人群和团体。这些个人、人群和团体对公共关系主体的生存、发展以及目标的实现,具有实际的或潜在的利害关系及客观存在的影响力。其实,公众与群众、人民、人群是完全不同的概念。即本质含义很大程度上是一致的,从范围上看,群众包括于人民之中,但其内涵更具体、稳定。......
2023-07-16
-
旅游的特点及定义-康养休闲旅游基础详细阅读
旅游作为人们日益喜爱的社会活动，具有区别于其他社会活动的鲜明特点。旅游是指人们离开常住地到异地所进行的旅行游览活动。暂时性表明旅游是在异地短暂停留的活动，结束后旅游者依然会回到自己的常住地工作和生活。为了便于统计，世界旅游组织规定旅游“暂时性”的时间长短以一年为限。因此，有些人到异国他乡打工、就业是不能称之为旅游的，虽然在此期间可能发生旅游的活动，但从整体来看不是旅游。......
2023-11-23
-
密度分布的特点及分析详细阅读
图2.49类杆流活性聚能侵彻体计算模型及观测点设置活性杆式射流成形过程及密度随时间的变化如图2.50所示。随着成形时间增至12 μs，药型罩底部局部密度开始下降。随着活性杆式射流分别到达炸高为2 CD、3 CD和4 CD处，侵彻体逐渐形成，整体密度降低，密度最高处仍集中于活性杆式射流头部外边缘，且由外至内、由头部至尾部，密度均逐渐下降。......
2023-06-18
-
保险的定义及分类的分析介绍详细阅读
保险正是针对危险而建立的一种经济制度。然而，保险也不可能对一切危险都予以承保。因此，将来确定发生的危险、已经发生的危险事故、投机性危险等均不被列入保险的适用范围。一旦发生被保险标的损失，由保险基金加以赔偿。人身保险是指以人的生命、身体或健康为保险标的的一种保险，如人寿保险、健康保险、意外伤害保险。原保险又称“第一次保险”“基础保险”，是指保险人对被保险人因保险事故所致损害承担......
2023-07-27
-
副流的特点及影响分析详细阅读
副流与紊流内部的漩涡不同，它的规模大，旋转中心和位置是稳定的、明显的。副流的存在，往往是河床冲淤的主要原因，对河道中设置人工构造物以后各种副流，必须予以注意。图6-6涵洞出口的平轴副流（立面图）图6-7桥台或丁坝附近的立轴副流（平面图）3.顺轴副流顺轴副流是顺主流方向呈螺旋形向前运动，又称为螺旋流。......
2023-11-20
-
矩阵秩的定义及性质分析详细阅读
【主要内容】1.矩阵秩的定义设A是m×n矩阵，则称A的不为零的子行列式（简称子式）的最高阶数为A的秩，记为r（A），其中，A的k（k≤min{m，n}）阶子式是指A的k行k列交叉位置的元素构成的k阶行列式.零矩阵的秩定义为0.2.矩阵秩的性质（1）设A是m×n矩阵，则0≤r（A）≤min{m，n}.（2）设A是m×n矩阵，k是常数，则（3）初等变换不改变矩阵的秩，即等价矩阵的秩相等.（4）设A，B......
2023-10-27
-
磨削方法及特点分析详细阅读
但由于后面部分磨粒的磨光作用，工件上残留面积大大减少，表面粗糙度较小。纵磨法是常见的一种磨削方法，可以磨削很长的表面，磨削质量好。图8－1纵磨法图8－2横磨法3.深磨法这种磨削法的特点是全部磨削余量在一次纵走刀中磨去。工件放在磨削砂轮和导轮之间，下方有一托板。磨削后平面的表面粗糙度的Ra值在0.2～0.8μm，尺寸可达IT5～IT6，对基面的平行度可达0.005～0.01mm／500mm。......
2023-07-01
相关推荐