c*与用拉普拉斯变换法分析连续系统的暂态响应相似，用Z变换法分析离散系统的暂态响应，根据闭环脉冲传递函数和输入信号，求出离散系统输出信号c*。例8-14 二阶系统如图8-21所示，求单位阶跃响应。，于是得离散时间c*-t图如8-22所示：1.闭环零、极点分布与暂态响应的一般关系离散系统的单位阶跃响应：图8-22例8-14二阶系统离散时间2.极点λi在z平面不同位置时的暂态响应情况极点λi在z平面不同位置时的暂态响应如图8-23所示。......
2023-06-28
离散系统稳定性分析
【摘要】：②K=5时，z2+1.792z+0.368=0解得z1=-0.237，z2=-1.555因为z2在单位圆外，所以系统是不稳定的。双线性变换，同时有分析离散系统的稳定性时，先令，代入离散系统的特征方程进行ω变换，再用劳斯判据判其稳定性。例8-16 设离散控制系统的方框图如图8-28所示。比较加采样开关前后系统的稳定性可知，采样开关的引入会使系统的稳定性变坏。
1.线性离散系统稳定的充要条件
闭环离散系统稳定的充要条件是闭环极点均在z平面上的单位圆内，即｜λi｜＜1。
2.s平面与z平面的映射关系
设 s=σ+jω 则z=eTs=eσT·ejωT
当σ=0，s=jω，z=1·ejωT
即s平面的虚轴映射为z平面上为以原点为圆心的单位圆周，为临界稳定区域。当σ＜0时，
，即左半s平面映射为z平面上单位圆内域，为稳定区域。如图8-26所示。
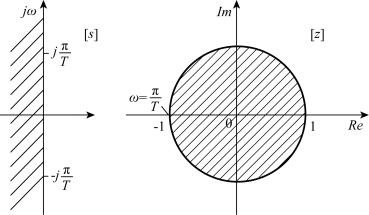
图8-26 s平面与z平面的映射关系
例8-15 如图8-27所示系统中，设采样周期T=1秒，试分析当K=4和K=5时系统的稳定性。
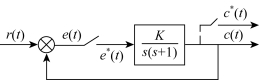
图8-27 例8-15系统结构图
开环脉冲传函为
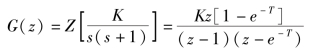
闭环脉冲传函为
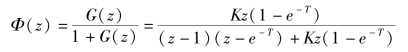
系统的闭环特征方程为
(z-1)(z-e-T)+Kz(1-e-T)=0
①K=4时，z2+1.16z+0.368=0
解得z1=-0.580+j0.178，z2=-0.580-j0.178
因为z在单位圆内，所以系统是稳定的。
②K=5时，z2+1.792z+0.368=0
解得z1=-0.237，z2=-1.555
因为z2在单位圆外，所以系统是不稳定的。
3.劳斯稳定判据在离散系统中的应用
离散系统不能直接使用劳斯稳定判据。需要采用ω变换，或称双线性变换，将z平面上单位圆周映射到新坐标系中的虚轴。
双线性变换
，同时有
分析离散系统的稳定性时，先令
，代入离散系统的特征方程进行ω变换，再用劳斯判据判其稳定性。
例8-16 设离散控制系统的方框图如图8-28所示。采样周期T=0.1s，试求使系统稳定的K的取值范围。
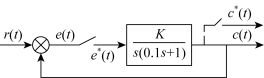
图8-28 例8-16离散控制系统的方框图
解：开环脉冲传递函数为
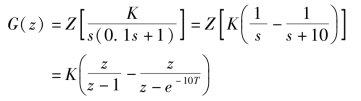
将T=0.1s代入上式可得
系统的闭环脉冲传递函数为 
系统的特征方程为1+G（z）=0，将G（z）代入上式，整理得
z2+(0.632K-1.386)z+0.368=0
令
，代入上式得
化简后得0.632Kω2+1.264ω+（2.736-0.632K）=0
根据上式写出劳斯表为
要使系统稳定，劳斯表中第一列各项系数均要大于零。即2.736-0.632K＞0所以0＜K＜4.32，使系统稳定K的取值范围为0～4.32。
比较加采样开关前后系统的稳定性可知，采样开关的引入会使系统的稳定性变坏。
有关自动控制原理的文章
- 详细阅读
-
稳定性刚体极限平衡分析成果详细阅读
根据野外调查和地质勘探资料，运用加拿大GEO-SLOPE公司开发的Geo-Studio系列软件中的SLOPE模块对林达滑坡进行稳定性刚体极限平衡分析。由于滑移线法的计算结果多数代表的是边坡稳定性状态的上限值，而垂直条分法的计算结果一般偏保守。表5.5-1滑坡稳定性计算工况汇总表根据稳定性系数的大小，可以确定边坡目前所处的稳定性状态。表5.5-2滑坡稳定性评价标准5.5.3.1天然工况分析成果主滑动体蓄水前天然工况下稳定性计算结果见表5.5-3。......
2023-08-20
-
相对稳定性分析方法与应用详细阅读
确定闭环系统的稳定性。例5-15 系统开环传递函数确定k=0.5、1、1.5、1.6时，闭环系统的稳态性能和暂态性能。闭环系统的稳定性可通过阶跃响应曲线加以验证。与上述结论一致。稳态特性分析例5-15中系统为Ⅰ型系统，则在阶跃输入信号下，稳态误差为零。暂态特性分析对稳定的系统，即K=0.5和K=1时，在伯德图中ωc1＜ωc2则有闭环系统的响应速度减慢，快速性变差。......
2023-06-28
-
路基稳定性与路基高度关系分析详细阅读
继续增加路基高度，从公式看出，若忽略黏聚力，边坡稳定性与路基高度已无关系。表3-2 沙漠地区路基边坡稳定性分析若坡度继续放缓、ω值继续变小，而稳定系数K会逐渐增大。......
2023-09-22
-
西部水电工程滑坡稳定性分析详细阅读
除前缘局部有小的崩滑产生外，黄草坪座落体目前整体稳定性较好。此外，座落体所处的大渡河谷地现今仍处抬升阶段，河流侧蚀作用相对较弱，除洪水期外，一般情况下对右岸岸坡堆积体的破坏较小，有利于座落体前缘堆积物的稳定。......
2023-08-20
-
检测装置性能及稳定性分析详细阅读
检测装置的基本性能是指仪器仪表的输出对输入的响应质量，包括静态特性和动态特性两大类。与量程有关的另一个指标是测量装置的过载能力，超过允许承受的最大输入量时，测量装置的各种性能指标得不到保证，这种情况称为过载。一般以室温条件下经过一个规定的时间后，测量装置的输出与起始标定时的输出差异程度来表示其稳定性。影响稳定性的因素主要是时间、环境、干扰和测量装置的器件状况。......
2023-06-22
-
合闸相角对电动稳定性的影响分析详细阅读
GB14048.2仅对短时耐受实验中不同电流下的功率因数、冲击系数等进行了要求，并未对合闸相角进行规定。这主要是因为电流相间邻近效应主要体现在某相电流峰值时其他两相电流在该相导体内的感应电流方向，而合闸相角的改变不影响三相电流的相序，故其不影响某相电流峰值时其他两相电流在该相导体内的感应电流方向。......
2023-06-15
- 详细阅读
相关推荐