首页理论教育离散系统暂态响应分析

离散系统暂态响应分析

2023-06-28 理论教育版权反馈

【摘要】：c*与用拉普拉斯变换法分析连续系统的暂态响应相似，用Z变换法分析离散系统的暂态响应，根据闭环脉冲传递函数和输入信号，求出离散系统输出信号c*。例8-14 二阶系统如图8-21所示，求单位阶跃响应。，于是得离散时间c*-t图如8-22所示：1.闭环零、极点分布与暂态响应的一般关系离散系统的单位阶跃响应：图8-22例8-14二阶系统离散时间2.极点λi在z平面不同位置时的暂态响应情况极点λi在z平面不同位置时的暂态响应如图8-23所示。

c*（t）与用拉普拉斯变换法分析连续系统的暂态响应相似，用Z变换法分析离散系统的暂态响应，根据闭环脉冲传递函数和输入信号，求出离散系统输出信号c*（t）。根据输出信号c*（t），可求出超调量Mp，调节时间ts等性能指标。

例8-14 二阶系统如图8-21所示，求单位阶跃响应。

pagenumber_ebook=255,pagenumber_book=244

图8-21　例8-14二阶系统的结构图

解：系统闭环脉冲传递函数为

pagenumber_ebook=255,pagenumber_book=244

取z反变换得

C(z)=0.368z-1+z-2+1.4z-3+1.4z-4

+1.147z-5+0.895z-6+0.802z-7+…

c*(t)=0.368δ(t-T)+δ(t-2T)+1.4δ(t-3T)+1.4δ(t-4T)+1.147δ(t-5T)

c*（t）+0.895δ（t-6T）+0.802δ（t-7T）+…，于是得离散时间c*-t图如8-22所示：

1.闭环零、极点分布与暂态响应的一般关系

离散系统的单位阶跃响应：

pagenumber_ebook=255,pagenumber_book=244

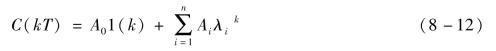
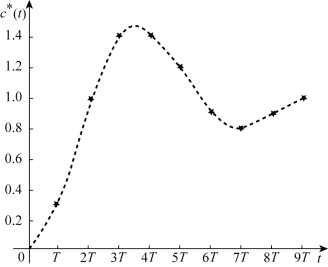
pagenumber_ebook=256,pagenumber_book=245

pagenumber_ebook=256,pagenumber_book=245

图8-22　例8-14二阶系统离散时间

2.极点λi在z平面不同位置时的暂态响应情况

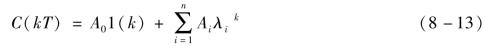
pagenumber_ebook=256,pagenumber_book=245

极点λi在z平面不同位置时的暂态响应如图8-23所示。

（1）λi为正实数

输出采样信号的暂态分量为

当λi＞1时，ci（k）为发散的指数函数，λik随着k的增加而增加。

当λi＜1时，ci（k）为衰减的指数函数，λi距坐标原点越近，λik衰减越快。

（2）λi为负实数

当k为偶数时，λik为正；当k为奇数时，λik为负。随着k增加，λik符号交替变化。当｜λi｜＞1时，ci（k）为发散振荡；当｜λi｜＜1时，ci（k）为衰减振荡，振荡的角频率为π/T。

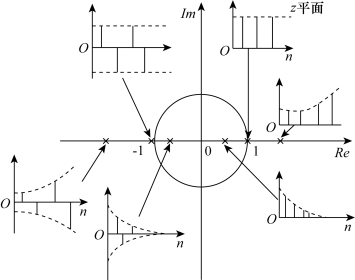
pagenumber_ebook=256,pagenumber_book=245

图8-23　闭环实极点分布与相应的动态响应形式

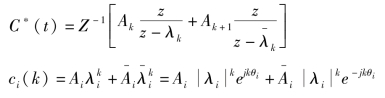
（3）有一对共轭复数极点λi和 pagenumber_ebook=257,pagenumber_book=246

pagenumber_ebook=257,pagenumber_book=246

又因为

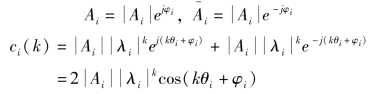
pagenumber_ebook=257,pagenumber_book=246

当｜λi｜＞1时，ci（k）为发散振荡函数；当｜λi｜＜1时，ci（k）为衰减振荡函数，如图8-24所示。

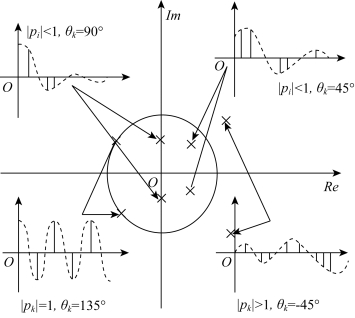
pagenumber_ebook=257,pagenumber_book=246

图8-24　闭环实极点分布与对应的动态响应形式

3.闭环脉冲传递函数的极点在z平面上的位置决定相应暂态分量的性质和特点

pagenumber_ebook=257,pagenumber_book=246

图8-25　闭环脉冲传递函数的极点在z平面上的位置与对应暂态分量

由图8-25可知，在离散系统设计时，应把闭环极点安置在z平面的右半单位圆内，且尽量靠近原点。