式中的系数Z11、Z12、Z21、Z22具有阻抗性质，所以式称为阻抗方程或Z方程。由此得出即Z12是输入端口开路时的转移阻抗，称为开路转移阻抗。无源线性二端口网络如果同时满足式 时，则Z参数中只有两个参数是独立的。......
2025-09-29
用Z变换求解差分方程
【摘要】：离散系统的动态过程用建立在差分、差商等概念基础上的差分方程来描述。k阶线形差分方程的一般形式为式中，r——输入量；c——输出量。各阶差分的变换函数例8-7 用Z变换法求二阶差分方程：y（k+2）+3y（k+1）+2y=r。解：利用超前定理，对差分方程进行Z变换，得z2Y-z2y-zy+3[zY-zy]+2Y=R将已知条件代入上式，得所以，利用部分分式法求Y的Z反变换所以，作Z 反变换，
离散系统的动态过程用建立在差分、差商等概念基础上的差分方程来描述。
1.差分的概念
差分与连续函数的微分相对应，分为前向差分和后向差分。
一阶前向差分 Δy（nT）=y[（n+1）T]-y（nT）
k阶前向差分 Δky（nT）=yk-1[（n+1）T]-yk-1（nT）
一阶后向差分 ∇y（nT）=y（nT）-y[（n-1）T]
k阶后向差分 ∇ky（nT）=yk-1（nT）-yk-1[（n-1）T]
2.差分方程
若方程的变量除了含有f（k）本身外，还有f（k）的各阶差分，则此方程称为差分方程。
k阶线形差分方程的一般形式为
式中，r（nT）——输入量；c（nT）——输出量。(https://www.chuimin.cn)
各阶差分的变换函数
例8-7 用Z变换法求二阶差分方程：y（k+2）+3y（k+1）+2y（k）=r（k）。
其初始条件y（0）=0，y（1）=1，输入为单位阶跃函数。
解：利用超前定理，对差分方程进行Z变换，得
z2Y(z)-z2y(0)-zy(1)+3[zY(z)-zy(0)]+2Y(z)=R(z)
将已知条件代入上式，得 
所以，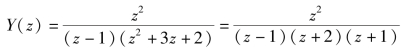
利用部分分式法求Y（Z）的Z反变换 
所以，
作Z 反变换，
相关文章
- 详细阅读
-
方程的离散求解方法详细阅读
图5-107控制体积法节点布局示意图5.5.3.2泥沙方程离散和求解悬移质输运方程离散和求解。悬沙输运方程和水流模型中的k、ε方程形式基本相同，只是在悬移质输运方程中多了一个下沉项，试算表明将下沉项作为源项比作为对流项更有利于求解的稳定。模型采用修正的QUICK 格式来离散悬沙输运方程的对流项，求解离散方程也采用ADI方法，相对于高阶格式所产生的离散方程的多余附加离散项采用显式离散，不存在求解困难。推移质输运方程的离散和求解。......
2025-09-29
-
根轨迹方程的求解方法详细阅读
系统的闭环特征方程为取其模值得模值方程为取其相角得相角方程为模值方程和相角方程成为根轨迹方程，从这两个方程可以看出，模值方程与增益K*有关，而相角方程与增益K*无关。所以，相角方程式决定闭环根轨迹的充分必要条件，而模值方程主要用来确定根轨迹上各点对应的开环增益值。，sn为闭环极点，在根轨迹图中用Δ表示。......
2025-09-29
-
用辅助平面法求解问题的方法和技巧详细阅读
为了方便、准确地作图，可选正平面为辅助面。当内表面由立体上的孔洞等结构形成时，内表面的相贯线画法与外表面的相贯线画法相同，只是其可见性要根据具体情况正确处理。图5-11两圆柱面正交的三种形式例5-3用辅助平面法求半球与圆柱体的截交线，如图5-12所示。根据积聚性可知，相贯线的俯视图积聚在圆柱体的圆周上，这时相贯线的正面投影要选辅助平面来求。图5-13相贯线的简化画法作图时注意，圆弧应向大圆柱体投影内弯曲。......
2025-09-29
-
机构运动分析及运动学方程求解详细阅读
10-1 如图10-19 所示机构中，椭圆规尺长AB=40 cm，曲柄长OC=20 cm，且AC=CB。如曲柄以匀角速度ω=πrad/s 绕O 轴转动，且已知AM=10 cm，求尺上M 点的运动方程和轨迹方程；t=0 和t=0.5 s 时的M 点的速度和加速度。图10-19题10-1图图10-20题10-2图10-3 如图10-21 所示，列车沿半径为R=800 m 的圆弧轨道做匀加速运动。图10-21题10-3图10-4 荡木用两条等长的钢索平行吊起，如图10-22 所示。......
2025-09-29
-
坐标变换与变换矩阵详细阅读
坐标变换的思路是，将交流电动机的物理模型等效地变换成类似直流电动机的模式，这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件，电流变换矩阵也就是电压变换矩阵，也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式，C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2025-09-29
-
超静定结构：未知力不能用平衡方程求解的结构详细阅读
静定结构和超静定结构的概念已在第十一章中作过介绍。相反，一个结构，如果其所有的未知力不能仅用平衡方程确定，则这种结构称为超静定结构。此连续梁有四个支座反力，而平衡方程却只有三个，仅用平衡方程不能求解，因此截面内力也就无法确定，所以它是一个超静定结构。图14-2超静定结构的类型......
2025-09-29
-
卡洛变换详解详细阅读
离散卡-洛变换是根据信号的统计特性性质进行正交展开。由式表示的变换称为离散卡-洛变换，系数向量g是信号向量通过该正交变换得到的，称之为主成分信号向量。离散卡-洛变换主要用于遥感多光谱信号中特征选择及数据压缩方面。因为是λi单调递减的，如果所选M个特征向量与M个最大特征值对应，那么用式来重建信号向量的误差最小，所以在最小均方误差的意义上讲，离散卡-洛变换是最优的。......
2025-09-29
相关推荐