MATLAB信号处理箱覆盖了经典信号处理理论的大多数内容，是一个非常优秀的算法研究和辅助设计工具。Simulink是MATLAB中的一种可视化仿真工具，是一种基于MATLAB的框图设计环境，是实现动态系统建模、仿真和分析的一个软件包，被广泛应用于线性系统、非线性系统、数字控制及数字信号处理的建模和仿真中。MATLAB画出的图像如图1-9所示。......
2023-06-23
MATLAB在非线性系统分析中的优越应用
【摘要】：本节主要讨论MATLAB在描述函数法分析中的应用。振荡频率与振荡幅值如图7-42可知分别为（方法二）线性部分的频率特性为具有死区继电特性的描述函数及相对描述函数：在程序文件方式下执行以下MATLAB程序OK1.m，在同一复平面上绘制非线性特性的相对负倒描述函数与线性部分的Nyquist曲线。非线性系统自激振荡时有运行以下程序，由，求自激振荡的振幅X。
本节主要讨论MATLAB在描述函数法分析中的应用。
例7-12 已知具有死区继电特性的非线性控制系统如图7-41所示，其中继电特性参数为M=1.7，死区特性参数为Δ=0.7，应用描述函数法作系统分析系统是否存在自激振荡？若有自激振荡，须求出自激振荡的振幅x与角频率ω。
图7-41 具有死区继电特性的非线性控制系统结构图
解：（方法一）
（1）带死区的继电型非线性环节的描述函数为
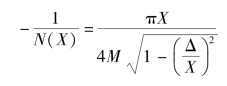
其负倒数函数为
当X为变量，由Δ开始增加时，
曲线从负无穷处出发沿负实轴增加，相角始终为-π，所以
曲线位于平面G0（jω）的负实轴上，幅值大小
随着X的增加先减后增，在X增加到
时，有极大值。
作
曲线。
（2）在图上作G（jω）曲线，当ω=140时，G（jω）曲线穿过实轴。
（3）当M=1.7，Δ=0.7时，
曲线的端点值为
因此，曲线与
在1.56e-jπ处两次相交，两次相交的X值分别为
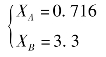
具有死区继电特性非线性系统的G（jω）曲线和
曲线关系如图7-42所示。
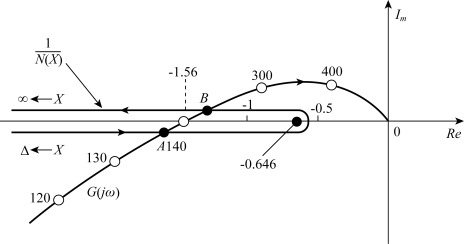
图7-42 具有死区继电特性非线性系统的G（jω）曲线和
曲线
对于A点邻域，被G（jω）曲线包围的段上，X是增幅的；不被G（jω）曲线包围的段上，X是减幅的。因此在A点邻域，扰动作用使得系统的运动脱离A点，而在B点邻域两边的运动，基于奈氏稳定性判据而形成自激振荡。振荡频率与振荡幅值如图7-42可知分别为
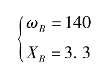
（方法二）
（1）线性部分的频率特性为
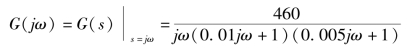
（2）具有死区继电特性的描述函数及相对描述函数：
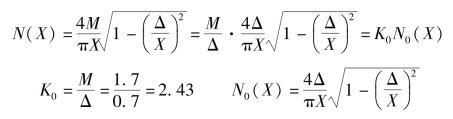
（3）在程序文件方式下执行以下MATLAB程序OK1.m，在同一复平面上绘制非线性特性的相对负倒描述函数与线性部分的Nyquist曲线。
运行该程序，在同一复平面上绘制非线性特性的相对负倒描述函数与线性部分的Nyquist曲线如图7-43所示。
图7-43 相对负倒描述函数与Nyquist曲线
由于具有死区继电特性的描述函数是自激振荡振幅X的实函数，其相对负倒描述函数也是自激振荡振幅X的实函数，其虚部为零，曲线在负实轴上，与系统线性部分Nyquist曲线的交点也在横坐标上。
（4）利用交点在横坐标上，其虚部为零，求交点的角频率ω与交点的
。
分母有理化后，运行以下程序，由上式分子虚部为零求交点的角频率ω。
symswn;
n=simple(j*(1-0.01*j*w)*(1-0.005*j*w))
运行结果为
n=i+3/200*w-1/20000*i*w^2
交点虚部为零，运行以下程序求交点的角频率ω。
[w]=solve(‘1-1/20000*w^2=0’)
程序运行结果：
w=[100*2^(1/2)]
[-100*2^(1/2)]
即交点的角频率ω=141.4rad/s。
运行以下程序，将ω=141.4rad/s代入线性部分的频率特性计算交点的K0G（j141.4）。
程序运行结果：
A=3.7271
即交点的
（5）在此应用相对描述函数的概念。非线性系统自激振荡时有
运行以下程序，由
，求自激振荡的振幅X。
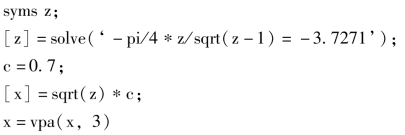
程序运行结果：x=
可见方法一与方法二所得结果非常接近。
有关自动控制原理的文章
- 详细阅读
-
MATLAB在时域分析中的优势及应用案例介绍详细阅读
本节将主要介绍如何利用MATLAB软件来分析线性控制系统的稳定性、输入响应及性能指标。下面给出时域分析时常用的MATLAB命令。例3-11 已知闭环系统传递函数为试用MATLAB判断系统的稳定性。图3-30例3-12系统的阶跃响应曲线图3-31例3-12系统的脉冲响应曲线例3-13 已知单位负反馈控制系统的开环传递函数为，试用MATLAB计算系统在单位阶跃信号作用下的tr、tp、ts、σ%。......
2023-06-28
- 详细阅读
-
MATLAB在电类专业课程中的应用及发展详细阅读
1984年，Cleve Moler和John Little成立了Math Works公司，发行了MATLAB 1.0版本，正式把MATLAB推向市场。1992年，MATLAB 4.0版本被发行。1994年，MATLAB 4.2c版本扩充了MATLAB 4.0版本的功能，在图形界面设计方面提供了新的方法。1999年，Math Works公司推出MATLAB 5.3版本，该版本在很多方面进一步改进了MATLAB语言的功能。2000年10月底，Math Works公司推出了全新的MATLAB 6.0版本，在核心数值算法、界面设计、外部接口、应用桌面等诸多方面有了极大的改进。......
2023-11-02
- 详细阅读
-
DHT在分布式数据库技术中的性能优越详细阅读
DHT虽简单，但性能优越。DHT无需中心服务器，分布式系统中所有的DHT节点是平等的。同时，DHT继承了哈希表的主要特性，如高效定位和搜索元素。这允许DHT灵活扩展到拥有很多节点。DHT由以下两部分组成。这个基本性质使得DHT在节点加入或离开网络时的重组需求变得最小。节点按照DHT的连接策略选择邻居。DHT必须具有以下三个特性。因为DHT具备这三个特性，所以它在一些领域大受青睐。......
2023-10-28
-
非线性算子的性质及应用详细阅读
非线性算子的性质包括连续性、有界性、全连续性、可微性等.这是一些基本概念和性质,在后面各章中都要用到.设E1和E2时两个实Banach 空间,D E1.设A∶D→E2为非线性的.定义1设x0∈D.若ε>0,δ=δ(x0,ε)>0 使得当x ∈D且‖x-x0‖ < δ 时,恒有‖Ax -Ax0‖ < ε,则称A 在x0连续;若A 在D 中每一点都连续,则称A 在D 上连续;若上述δ 只与ε 有关而......
2023-10-20
-
水在岩土体中的存在形式及其在工程中的应用详细阅读
因此，在潜水面以上常形成毛细水带。图1-3各种形态的水在岩层中的分布气态水、结合水、毛细水和重力水在地壳最表层岩土中的分布有一定的规律性。当在松散岩土中开始挖井时，岩土是干燥的，但是实际上存在着气态水和结合水；继续向下挖，发现岩土潮湿，说明岩土中有毛细水存在；再向下掘进，便开始有水渗入井中，并逐渐形成地下水面，这就是重力水。......
2023-09-23
相关推荐