下面对这些评价理论和方法作一扼要介绍。效用理论就是用数学方法描述效用和效用函数的关系，并根据评价者给定的效用值的大小进行方案评价。......
2023-07-15
非线性系统相平面分析：理论及方法
【摘要】：应用线性系统相平面分析的方法和结论，绘出各区域的相轨迹。例7-8 设一阶非线性系统的微分方程为试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。图7-37系统相平面图例7-10 具有饱和非线性特性的控制系统如图7-38所示，试用相平面法分析系统的阶跃响应。
1.非线性系统的相平面分析法的一般步骤
（1）根据非线性特性的分段情况，用几条分界线将相划分为几个现行区域。
（3）应用线性系统相平面分析的方法和结论，绘出各区域的相轨迹。
（4）根据系统状态变化的连续性，在各区域的交界线上，将相轨迹彼此衔接成连续曲线，即构成完整的线性系统相平面图。
（5）根据所得的非线性微分方程的相轨迹讨论系统的稳定性与稳态误差。
2.分析中的关键术语
（1）开关线或转换线：将各线性区域的分界线称为开关线。
（2）转换点：在开关线上相轨迹发生改变的点。
（3）实奇点：每个区域内有一个奇点，如果这个奇点在本区域之内，这种奇点称实奇点。
（4）虚奇点：如果奇点落在本区域之外，称为虚奇点。
表明该区域相轨迹不可能汇集于虚奇点。二阶非线性系统中，只可能有一个实奇点，而与这个实奇点所在区域邻接的所有其他区域都可能有虚奇点。
例7-8 设一阶非线性系统的微分方程为
试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。
解：令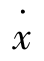
=0得
-x+x3=x(x2-1)=x(x-1)(x+1)=0
系统平衡状态
xe=0,-1,+1
式中，xe=0：稳定的平衡状态；
xe=-1，+1：不稳定平衡状态。
计算列表7-5，画出相轨迹如图7-35所示。
图7-35 系统的相轨迹
表7-5
可见，当
时，系统最终收敛到稳定的平衡状态；当
时，系统发散；x（0）＜-1时，x（t）→-∞；x（0）＞1时，x（t）→∞。
注：系统为一阶，故其相轨迹只有一条，不可能在整个
～x平面上任意分布。
例7-9 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。
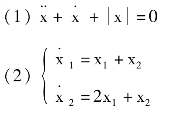
解：（1）系统方程为
令
，得平衡点：xe=0。
系统特征方程及特征根：
计算列表7-6。
表7-6
用等倾斜线法绘制系统相平面图如图7-36所示。
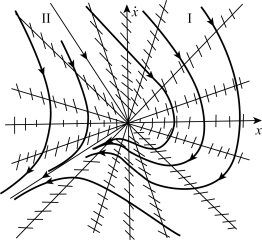
图7-36 例7-9系统相平面图
（2）系统方程为
由式①得：
式③代入②得：
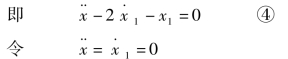
得平衡点：xe=0
由式④得特征方程及特征根为
画相轨迹，由④式得
计算列表7-7。
表7-7
用等倾斜线法绘制系统相平面图如图7-37所示。
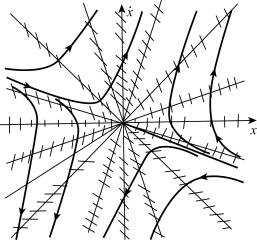
图7-37 系统相平面图
例7-10 具有饱和非线性特性的控制系统如图7-38所示，试用相平面法分析系统的阶跃响应。
解：非线性特性的数学表达式为
线性部分的微分方程式为
考虑到r-c=e，上式又可以写成
输入信号为阶跃函数，在t＞0时有，
，因此有
根据已知的非线性特性，系统可分为三个线性区域。
Ⅰ区：系统的微分方程为
按前面确定奇点的方法，可知系统在该区有一个奇点（0，0），奇点的类型为稳定焦点。图7-38（a）为Ⅰ区的相轨迹，它们是一簇趋向于原点的螺旋线。
Ⅱ区：系统的微分方程为
设一般情况下，初始条件为e（0）=e0，
则上式的解为
对上式求一次导数，得
故当初始条件e′0=-KM时，相轨迹方程为e′=-KM。
当e′0≠-KM时，相轨迹方程为
由此可作出该区的相轨迹，如图7-38（b）所示，相轨迹渐进于直线
=-KM。
Ⅲ区：此时系统的微分方程为
将Ⅱ区相轨迹方程中的KM改变符号，即得Ⅲ区的相轨迹方程
该区的相轨迹如图7-38（b）所示。
将以上各区的相轨迹连接起来，便是系统的整个相平面图，如图解7-38（c）所示。
假使系统原来处于静止状态，则在阶跃输入作用时，相轨迹的起始点应为e（0）=R，
（0）=0。此时的系统的相平面图如图7-38（d）所示。由图可知，系统在阶跃输入作用时，系统是稳定的，其稳态误差为零。动态过程具有衰减振荡性质，最大超调量可从图中量得。
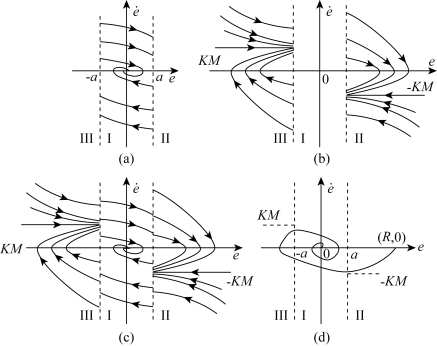
图7-38 非线性系统的相平面图
例7-11 含有继电特性的非线性控制系统结构如图7-39所示，系统可采用下面的一组方程来描述。
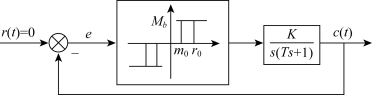
图7-39 含有继电特性的非线性控制系统
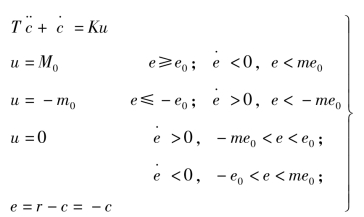
当研究系统的自由运动时，r=0，注意到e=-c，
，可以把非线性系统转变为按输出c来分段，则上述方程组可改写为
设：K=0.1，e0=20，m=0.5，M0=380，T=0.5。
我们在（c-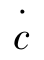
）相平面上画相轨迹，如图7-40所示。
图7-40 相平面图（m=0.5）
下面讨论系统的几个主要参数对系统运动的影响。
（1）继电特性的回差（数值m）对系统运动的影响。
继电特性的m值可以取-1到+1间任何一个数值。
m值的减小使相轨迹从相平面的一个区域转换到另一区域的时间后移，转换时的速度（
）的绝对值增大，加剧了运动的振荡过程。在某一m值下，相平面图上会出现一个稳定的极限环，系统的运动最后成为稳定的等幅振荡。在这种情况，系统不能正常工作。
（2）线性部分的时间常数和传递系数对系统运动的影响。
在相平面的Ⅰ区，相轨迹是直线，其斜率为-1/T。当T增加时，斜率的绝对值减小，相轨迹变平。这将会加剧运动的振荡过程。K的增大使在Ⅱ，Ⅲ区的相轨迹的渐近线离相平面的横轴越远。这样，当相轨迹从相平面的一个区域转移到另一个区域时有较大的速度（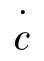
）的绝对值增大。所以，K的增大会加剧运动的振荡过程。
综上所述，相平面法一般可解决下列问题：
（1）相平面上可以清晰地表示出系统在各种初始条件下的所有可能的运动；
（2）相平面上可用奇点来分析系统的稳定性；
（3）相平面上可用极限环来分析系统的自振稳定性；
（4）由相轨迹可以求出系统的瞬态响应。
上面介绍的相平面分析法原则上仅适用于二阶系统。但是，相平面分析法的概念可以扩展到高阶系统中去。对三阶系统，在三维空间内图解作图比较困难，而当阶数高于三阶时，绘出描述运动的相轨迹是不可能的。现代控制理论的状态空间分析法适用于在n维空间内对系统进行动态分析和综合，它是相平面法的推广。
有关自动控制原理的文章
- 详细阅读
-
炮控伺服系统非线性因素分析详细阅读
对火炮随动系统来说，低速不平稳将导致不能准确地跟踪目标。测量元件不工作在死区，这时，系统处于开环状态。应该尽量使伺服系统工作在线性区，同时保证系统响应快速、平稳。其中，坦克减速器齿轮的啮合间隙是一种不可忽视的非线性因素。......
2023-06-24
-
相平面与相轨迹的基本概念详细阅读
相平面上的状态点随时间变化描绘出来的曲线称为相轨迹。由此，在相平面上将布满与不同的初始条件相对应的一簇相轨迹。相平面图直观地表明一阶或二阶系统在各初始条件下的运动过程。相平面法与描述函数法不同，描述函数法实质是令系统线性部分不动，而将其非线性部分线性化。为了便于理解相平面及相轨迹等概念，下面举例说明。图7-27例7-6系统的相平面图该图为具有不同起始点一簇同圆心的相轨迹。......
2023-06-28
-
平面力系合成与平衡的方法分析详细阅读
平面汇交力系合成的几何法设一刚体受到平面汇交力系F1、F2、F3、F4 的作用，各力的作用线汇交于一点A。若平面汇交力系有n 个力，用FR 表示合力矢，则有合力矢对刚体的作用与原力系对该刚体的作用是等效的。图3-17几何法求约束力根据平面汇交力系平衡的几何条件，此3 个力可以组成一个封闭的三角形。......
2023-06-26
-
三相系统短路时的电动力分析详细阅读
若，当φ=φ-105°，ωt=π时，A、C相导体受到的最大电动斥力为-2.65F0；B相导体受到的最大吸力和斥力值相同，达到最大值的时刻不同，其值为±2.8F0，发生在φ=φ-45°，ωt=π时。对于等边三角形布置的三相导体，如令短路电流的衰减系数，则A相导体最大电动力发生在φ=φ-90°时，其变化规律为B相、C相导体与A相导体受力相同，只是时间、空间相位不同。......
2023-06-30
-
物相衍射分析方法与应用详细阅读
对于混合物来说，各个晶相的衍射花样会同时出现，而不会出现干涉。X射线物相分析可以鉴别样品中的物相，包括纯元素（单质）、化合物和固溶体。同一种材料，可以具有不同的物相，称为同分异构体。就广义而言，物相衍射分析包括物相鉴定、定量分析、相结构的测定以及相变过程检测等。但对于纳米材料，晶粒的小尺寸会导致衍射峰的宽化，进而影响积分强度的计算，所以纳米材料定量分析的精度和准确度都远低于传统材料。......
2023-06-20
-
MATLAB在非线性系统分析中的优越应用详细阅读
本节主要讨论MATLAB在描述函数法分析中的应用。振荡频率与振荡幅值如图7-42可知分别为（方法二）线性部分的频率特性为具有死区继电特性的描述函数及相对描述函数：在程序文件方式下执行以下MATLAB程序OK1.m，在同一复平面上绘制非线性特性的相对负倒描述函数与线性部分的Nyquist曲线。非线性系统自激振荡时有运行以下程序，由，求自激振荡的振幅X。......
2023-06-28
-
三相对称系统中的功率分析详细阅读
在三相对称系统中，总的有功功率、无功功率和总视在功率一般都是按3倍的单相功率来进行计算的。因为，在三相电路和单相电路中，无功功率的描述并不是一致的。在三相系统中，三相瞬时有功功率恒定且等于3倍的单相有功功率。因而，当把三相系统作为整体考虑时，将三相无功功率设想成代表一个电源和负载之间的振荡能量流是不正确的。......
2023-06-23
相关推荐