系统的闭环特征方程为取其模值得模值方程为取其相角得相角方程为模值方程和相角方程成为根轨迹方程，从这两个方程可以看出，模值方程与增益K*有关，而相角方程与增益K*无关。所以，相角方程式决定闭环根轨迹的充分必要条件，而模值方程主要用来确定根轨迹上各点对应的开环增益值。，sn为闭环极点，在根轨迹图中用Δ表示。......
2025-09-29
绘制相轨迹的方法
【摘要】：常用相轨迹的绘制方法主要有解析法、图解法和实验法。解析法是先求微分方程的解，然后再绘制相轨迹的方法，如例7-6的解法。图解法是一种不必求出微分方程的解，而是通过某种逐步作图的顺序，直接在相平面上画出相轨迹的方法。利用等倾线分布图绘制相轨迹。在每条等倾斜线上画出相应的a值短线，所有短线的总体就形成了相轨迹的切线方向场。对照图7-28和图7-27可见，相轨迹是个圆，和解析法得到的结果一样。图7-28例7-7系统相轨迹
常用相轨迹的绘制方法主要有解析法、图解法和实验法。解析法是先求微分方程的解，然后再绘制相轨迹的方法，如例7-6的解法。本节着重介绍应用图解法绘制相轨迹。图解法是一种不必求出微分方程的解，而是通过某种逐步作图的顺序，直接在相平面上画出相轨迹的方法。当微分方程用解析法求解比较复杂、困难甚至不可能时，对于非线性系统，图解法尤为重要。图解法有等倾线法、圆弧近似法（δ法）多种，本节仅介绍等倾线法。等倾线法的基本思想是：先确定相轨迹的等倾线，进而绘出相轨迹的切线方向场，如果我们能用简便的方法确定出相平面中任意一点相轨迹的斜率，则该点附近的相轨迹便可用过这点的相轨迹切线来近似。然后从初始条件出发，沿方向场逐步绘制相轨迹。
由于
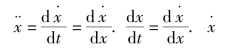
则，
式中，d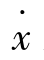
/dx表示相平面上相轨迹点（x（t），
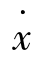（t））切线的斜率，若取斜率为常数，则该式可改写成
该式称为相轨迹的等倾线方程。对于相平面上满足上式的各点，经过它们的相轨迹的斜率都等于a，若将这些具有相同斜率的点连成一线，则此线称为相轨迹的等倾线。
利用等倾线法绘制相轨迹的一般步骤如下。
（1）由给定系统求出式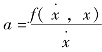
的等倾线方程。
（2）根据等倾线方程在相平面上画出等倾线分布图，给定不同的a值，尽可能多地在相平面上画出不同的等倾线。一般地，等倾线的条数愈多，作图精度愈高。
（3）在每条等倾线上标明其对应的a值切线方向场。
（4）利用等倾线分布图绘制相轨迹。即从初始点出发，沿着“切线方向场”各点切线方向将这些短线段用光滑的曲线连接起来，便得到系统的一条相轨迹。(https://www.chuimin.cn)
下面通过具体例子说明如何用等倾斜线法绘制相轨迹。
例7-7 利用等倾斜线法绘制例7-6系统的相轨迹。
解：已知系统的微分方程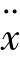
=-x。
由式（7-8）可以写出该系统的相轨迹方程为
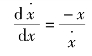
令
，则等倾线方程为
显然，等倾线是通过相平面坐标原点的直线，其斜率为
而a是相轨迹通过等倾线时切线的斜率。令a为不同的值，就可以求出不同的β值，见表7-2。
表7-2 β与a的关系值表
据此可以绘出具有不同斜率的一簇等倾斜线，见图7-28。在每条等倾斜线上画出相应的a值短线，所有短线的总体就形成了相轨迹的切线方向场。假设初始条件为x（0）=x0，x（0）=0，则可以从起点（x0，0）出发，沿方向场绘制出系统的相轨迹。对照图7-28和图7-27可见，相轨迹是个圆，和解析法得到的结果一样。
图7-28 例7-7系统相轨迹
相关文章
- 详细阅读
-
PCB库的绘制技巧与方法详细阅读
进行以下操作进入PCB库绘制界面，如图5-10和图5-11所示。PCB的常用绘制工具包括线放置工具、焊盘放置工具、过孔放置工具、字符放置工具、坐标放置工具、测量工具、几何图形放置工具和阵列粘贴工具。图5-12 进入PCB库绘制界面图5-13 PCB库常用绘制工具在绘制PCB库图时需要先选择工作层，再在层上作图。禁止布线层一般不在PCB库文件中应用，一般是作为PCB文件的中的PCB开槽和PCB外框绘制。图5-14 PCB库封装重命名图5-15 PCB库封装属性的修改......
2025-09-29
-
如何绘制三相电路图形符号详细阅读
“三相电路”图形符号主要包括字符和直线，其符号编码为S00005，主要应用于电路图、接线图和功能图中。下面介绍如何绘制该图形符号。图6-19 指定两个对角点图6-19 指定两个对角点图6-20 绘制一处字符组图6-20 绘制一处字符组操作技巧：要输入平方字符，则可在“文字编辑器”上下文选项卡的“插入”面板中单击“符号”按钮，接着从打开的符号下拉菜单中选择“平方”选项。图6-21 绘制另外一处字符组图6-21 绘制另外一处字符组......
2025-09-29
-
正轴测投影的绘制方法详细阅读
此时在P面上所得到的投影称为正等轴测投影，简称正等测。这样便可按实际尺寸画图，但画出的图形比原轴测投影大些，各轴向长度均放大1/0.82≈1.22倍。图5-6斜垫块的正投影图5.2.1.2平面体的正等轴测投影的画法已知斜垫块的正投影图，画出其正等测图，如图5-6所示。如图5-13 所示，作楔形板上、下底面的轴测投影。......
2025-09-29
-
绘制圆弧曲线的技巧与方法详细阅读
图4-5圆心、半径或直径画圆图4-6三点画圆以“两点”方式绘制圆。在下拉菜单中单击:“绘图”→“圆弧”。图4-11几种圆弧的画法以“三点”方式绘制圆弧。2)起点、圆心、角度:指定圆弧的起点、圆心、角度来绘制圆弧。......
2025-09-29
-
装配图的图形绘制方法详细阅读
装配图制定了一些规定画法和特殊画法，下面将分别进行介绍。单独表达某个零件的画法：在装配图中，当某个零件的主要结构在其他视图中未能表示清楚，而该零件的形状对部件的工作原理和装配关系的理解起着十分重要的作用时，可单独画出该零件的某一视图。......
2025-09-29
-
有效计算非全相断线的方法与技巧详细阅读
电力系统的短路故障通常称为横向故障，它指的是在网络的节点f处出现了相与相之间或相与零电位点之间不正常接通的情况。发生横向故障时，由故障节点f同零电位节点组成故障端口。造成非全相断线的原因很多，例如某一线路单相接地短路后故障相开关跳闸；导线一相或两相断线；分相检修线路或开关设备以及开关合闸过程中三相触头不同时接通等。图12-18用对称分量法分析非全相运行......
2025-09-29
-
计算换相重叠角的方法及应用详细阅读
根据以上分析及结果，再经进一步分析可得出以下变压器漏感对整流电路影响的一些结论：①出现换相重叠角γ，整流输出电压平均值Ud 降低。⑤换相使电网电压出现缺口，成为干扰源。解因为换相压降的等效内阻又因为当α=0°时，cos γ=1-0.035=0.965，所以换相重叠角......
2025-09-29
相关推荐