常用相轨迹的绘制方法主要有解析法、图解法和实验法。解析法是先求微分方程的解,然后再绘制相轨迹的方法,如例7-6的解法。图解法是一种不必求出微分方程的解,而是通过某种逐步作图的顺序,直接在相平面上画出相轨迹的方法。利用等倾线分布图绘制相轨迹。在每条等倾斜线上画出相应的a值短线,所有短线的总体就形成了相轨迹的切线方向场。对照图7-28和图7-27可见,相轨迹是个圆,和解析法得到的结果一样。图7-28例7-7系统相轨迹......
2023-06-28
二阶时不变系统(可以是线性的,也可以是非线性的)一般可用下列常微分方程描述:
![]()
式中,f(x,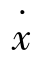 )是x(t)和
)是x(t)和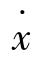 (t)的解析函数。方程式(7-17)的解既可以用x(t)与t的关系曲线表示,也可以将时间t作为参变量,用
(t)的解析函数。方程式(7-17)的解既可以用x(t)与t的关系曲线表示,也可以将时间t作为参变量,用 (t)和x(t)的关系曲线来表示。现以x(t)为横坐标,
(t)和x(t)的关系曲线来表示。现以x(t)为横坐标, (t)为纵坐标而组成的直角坐标平面称为相平面,这时系统在某一时刻t的状态就可以用相平面上的一个点(x,
(t)为纵坐标而组成的直角坐标平面称为相平面,这时系统在某一时刻t的状态就可以用相平面上的一个点(x,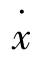 )来描述。t=0的初始条件为x(0)、
)来描述。t=0的初始条件为x(0)、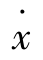 (0),其对应于相平面的一个初始点。状态随时间的转移对应于相平面上状态点的移动。相平面上的状态点随时间变化描绘出来的曲线称为相轨迹。对于不同的初始条件,根据解的存在与唯一性定理,微分方程必有不同的解与之一一对应。由此,在相平面上将布满与不同的初始条件相对应的一簇相轨迹。由这样一簇相轨迹所组成的相平面图像叫相平面图。相平面图直观地表明一阶或二阶系统在各初始条件下的运动过程。相平面法与描述函数法不同,描述函数法实质是令系统线性部分不动,而将其非线性部分线性化。相平面法是令系统非线性部分原封不动,而将高阶系统线性部分简化为二阶。所以上述两种方法各有侧重,互补长短,若同时用两种方法分析一个系统,则分析结果更加全面。对于二阶系统而言,它的某一状态都对应于相平面上的一个点,系统运动可以在相平面上表示出来。系统状态随时间的改变对应于相平面上点的移动。根据绘制出的x-
(0),其对应于相平面的一个初始点。状态随时间的转移对应于相平面上状态点的移动。相平面上的状态点随时间变化描绘出来的曲线称为相轨迹。对于不同的初始条件,根据解的存在与唯一性定理,微分方程必有不同的解与之一一对应。由此,在相平面上将布满与不同的初始条件相对应的一簇相轨迹。由这样一簇相轨迹所组成的相平面图像叫相平面图。相平面图直观地表明一阶或二阶系统在各初始条件下的运动过程。相平面法与描述函数法不同,描述函数法实质是令系统线性部分不动,而将其非线性部分线性化。相平面法是令系统非线性部分原封不动,而将高阶系统线性部分简化为二阶。所以上述两种方法各有侧重,互补长短,若同时用两种方法分析一个系统,则分析结果更加全面。对于二阶系统而言,它的某一状态都对应于相平面上的一个点,系统运动可以在相平面上表示出来。系统状态随时间的改变对应于相平面上点的移动。根据绘制出的x-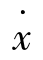 相轨迹图,研究非线性系统的稳定性和动态性能。
相轨迹图,研究非线性系统的稳定性和动态性能。
为了便于理解相平面及相轨迹等概念,下面举例说明。
例7-6 设二阶常微分方程:
![]()
求在初始条件t=0,x(0)=x0时的相平面图。
解:方程 =-x满足初始条件的解为
=-x满足初始条件的解为

当t=0,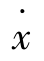 (0)=0,有
(0)=0,有
![]()
其相应的相平面图如图7-27所示。
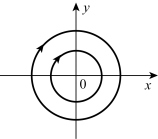
图7-27 例7-6系统的相平面图
该图为具有不同起始点(x0,0)一簇同圆心的相轨迹。图中箭头表示时间t增加时,状态点的运动方向。
有关自动控制原理的文章

常用相轨迹的绘制方法主要有解析法、图解法和实验法。解析法是先求微分方程的解,然后再绘制相轨迹的方法,如例7-6的解法。图解法是一种不必求出微分方程的解,而是通过某种逐步作图的顺序,直接在相平面上画出相轨迹的方法。利用等倾线分布图绘制相轨迹。在每条等倾斜线上画出相应的a值短线,所有短线的总体就形成了相轨迹的切线方向场。对照图7-28和图7-27可见,相轨迹是个圆,和解析法得到的结果一样。图7-28例7-7系统相轨迹......
2023-06-28

应用线性系统相平面分析的方法和结论,绘出各区域的相轨迹。例7-8 设一阶非线性系统的微分方程为试确定系统有几个平衡状态,分析平衡状态的稳定性,并画出系统的相轨迹。图7-37系统相平面图例7-10 具有饱和非线性特性的控制系统如图7-38所示,试用相平面法分析系统的阶跃响应。......
2023-06-28

为了与一般复数相区别,我们把表示正弦量的复数称为相量。 已知两支路并联的正弦交流电路中,支路电流分别为i1=8sinA,i2=6sinA,试求总电流i,画出电流相量图。解:首先将各支路电流用最大值相量表示为则利用复数的加法运算法可得根据相量与正弦量之间的对应关系,即可写出根据相量与正弦量之间的对应关系,即可写出电流相量图如图4.2所示。电流相量图如图4.2所示。......
2023-06-24

三相交流电的特点及使用,是电路分析中的一项重要内容。本章主要介绍三相电路中电压、电流的相值和线值之间的关系,对称和不对称三相电路的分析与计算方法,三相电路功率的计算和测量方法。进一步理解三相电路功率关系,熟练掌握两表法的功率测量方法,学会功率表的使用方法与接线规则。......
2023-06-24

有图7.9三相负载的三角形连接图7.9三相负载的三角形连接图7.10[例7.4]电路图图7.10[例7.4]电路图根据对称性得另外两相的线电流为根据对称性得另外两相的线电流为先求出负载端的相电压,再利用线电压和相电压的关系求出负载端的线电压。检验学习结果7.3.1 一台三相异步电动机正常运行时作△接,为了减小启动电流,启动时先把它作Y接,转动后再改成△接。......
2023-06-24

图7.4 为三相电源作△接的电路图,简称三角形电源。实际三相电源作△接时,如果接法正确,电源回路中没有电流。检验学习结果7.2.1 三相电源的相电压有效值为220V,若把X、Y连接,UAB等于多少?......
2023-06-24

液相冶金过程对焊缝金属的成分、性能、焊接质量以及焊接工艺性能都有很大影响。焊接液相冶金的最主要特点是:焊接时,不同的焊接方法对焊接区金属采用不同的方式进行保护。各阶段冶金反应的综合结果,就决定了焊缝金属的最终化学成分。......
2023-06-24
相关推荐