2）计算模型采用Midas Civil 软件进行整体结构受力分析。图3-6直沽桥空间计算模型3）静力分析进行全桥静力分析，考虑结构自重、车辆荷载、人群荷载、风荷载、整体升降温、局部温差以及各个墩位6 mm 的不均匀沉降等工况。分析结果表明，直沽桥主体结构设计满足抗震规范要求。计算结果表明，结构在恒载、满布汽车和人群荷载作用下，最小屈曲临界荷载系数为5.45，满足规范要求。......
2023-07-01
自激振荡的分析与计算
【摘要】：对于稳定的自激振荡，其振幅和频率是确定的，并可以测量得到。例7-3 具有理想继电器特性非线性系统结构如图7-21所示，试确定其自激振荡的幅值和频率。而线性部分的频率特性为要计算系统的自振荡的振幅和频率，就是求取两条曲线的交点处的幅值A及ω。由图可知，两曲线有一个交点，且对应于该交点的自激振荡是稳定的。为消除自激振荡，继电器特性参数应如何调整。
前已述及，若G（jω）曲线与-1/N（A）曲线相交，则系统将产生自激振荡。为对自激振荡的产生过程有更深入的理解，下面从信号的角度进一步分析自振荡产生的条件。
在如图7-10所示非线性系统中，若产生自激振荡，则意味着系统中有一个正弦信号在流通，不妨设非线性环节的输入信号为
x(t)=Asinωt
则非线性环节输出信号基波分量为
而线性部分的输出信号为
根据系统存在自振荡的假设，r（t）=0，故
x(t)=-c(t)
即
所以
自激振荡也存在一个稳定性问题，因此必须进一步研究自振荡的稳定性。若系统受到扰动偏离了原来周期运动状态，当扰动消失后，系统能够重新收敛于原来的等幅振荡状态，称为稳定的自振荡；反之，称为不稳定的自振荡。判断自振荡的稳定性可以从上述定义出发，采用扰动分析的方法。
以图7-20（c）为例，G（jω）与-1/N（A）曲线有两个交点，说明存在两个自激振荡点。对于M1点，若受到干扰使振幅A增大，则工作点将由点M1移至a点，此时a点不被曲线G（jω）包围。系统稳定，振荡衰减，振幅A自动减小，工作点将沿-1/N（A）曲线回到M1点。反之亦然，所以M1点是稳定的自激振荡。用同样的方法可以分析点M2是不稳定的振荡点。
按照下述准则来判断自激振荡的稳定性是极为简便的：在复平面上自激振荡点附近，当按幅值A增大的方向沿-l/N（A）曲线移动时，若系统从不稳定区进入稳定区，则该交点代表的是稳定的自激振荡；反之，若沿-l/N（A）曲线振幅A增大的方向是从稳定区进入不稳定区，则该交点代表的是不稳定的自激振荡。
对于稳定的自激振荡，其振幅和频率是确定的，并可以测量得到。计算时，振幅可由-l/N（A）曲线的自变量A的大小来确定，而振荡频率由G（jω）曲线的自变量ω来确定。
对于不稳定的自激振荡，由于实际系统不可避免地存在扰动，因此这种自振荡是不可能持续的，仅是理论上的临界周期运动，在实际系统中是测量不到的。
值得注意的是，由前面推导自振荡产生的条件时可知，对于稳定的自振荡，计算所得到的振幅和频率是图7-10中非线性环节的输入传号x（t）=Asinωt的振幅和频率，而不是系统的输出信号c（t）。
例7-3 具有理想继电器特性非线性系统结构如图7-21所示，试确定其自激振荡的幅值和频率。
图7-21 例7-3具有理想继电器特性非线性系统结构图
解：因为理想继电器的描述函数为
当A=0时，-l/N（A）=0；当A=∞时，-l/N（A）=-∞，因此-l/N（A）曲线就是整个负实轴区间如图7-20所示。而线性部分的频率特性为
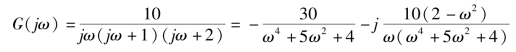
要计算系统的自振荡的振幅和频率，就是求取两条曲线的交点处的幅值A及ω。
由上式可以画出G（jω）曲线，如图7-20（a）所示。由图可知，两曲线有一个交点，且对应于该交点的自激振荡是稳定的。求G（jω）与-l/N（A）的交点，令
ImG（jω）=0得
，将其代入G（jω）的实部得
由此求得
例7-4 设控制系统的结构图如图7-22所示，图中死区继电器特性的参数为a=1，b=3。
（1）计算自激振荡的振幅和频率。
（2）为消除自激振荡，继电器特性参数应如何调整。
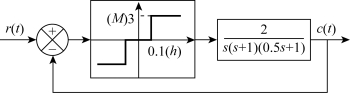
图7-22 例7-4具有死区继电器特性的控制系统结构图
解：（1）死区继电器特性的负倒数描述函数为
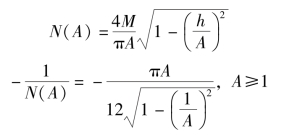
当A=1时，-1/N（A）=-∞；当A=∞时，-1/N（A）=-∞。其极值发生在A=2处，此时
因此，-1/N（A）是从负实轴上-π/6至-∞这一段，为清楚起见，用两条直线来表示，如图7-23所示。
图7-23 例7-4非线性控制系统的稳定性分析图
（2）为使系统不产生自激振荡，可通过调整继电器特性的死区参数来实现。此时，应使-1/N（A）的极值小于G（jω）曲线与负实轴的交点坐标，即
若取β=2，即调整为a=1.5，则-1/N（A）极值为-π/4=-0.785。显然，这时两条曲线不相交。从而保证系统不产生自振荡。
同样道理，也可以在不改变继电器特性参数的情况下。通过减小G（jω）的传递系数，使G（jω）曲线与负实轴的交点右移，使系统减小或消除自激振荡。
例7-5 试将如图7-24（a）和图7-24（b）所示两个非线性系统归一化为一个非线性部分和一个线性部分串联的典型结构。
图7-24 例7-5非线性系统结构图
解：图7-24（a）中，由于G1和G2构成一个内环负反馈，且等效于
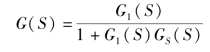
故如图7-24（a）所示非线性系统可归一化为如下典型结构如图7-25所示。
图7-25 两个非线性系统归一化结构图
图7-24（b）中，先将主反馈回路（外环）与G构成闭环回路，即变换为如图7-26所示。
图7-26 两个非线性系统归一化结构图
有关自动控制原理的文章
- 详细阅读
-
计算公式的分析与讨论详细阅读
分析认为对于较小的等标污染负荷，水库岸边污染混合区相对较窄，涉及水深较浅，污染物比较容易达到垂向混合均匀，所以这时污染混合区范围出现与二维理论求解得到的解析计算公式变化规律相同的情况；对于较大的等标污染负荷，水库岸边污染混合区相对较宽，涉及水深较大，污染物不容易达到垂向混合均匀，所以这时污染混合区范围出现与本文三维理论求解得到的解析计算公式变化规律相同的情况。......
2023-06-26
-
云计算与网格计算的差别及应用分析详细阅读
云计算和网格计算都是由分布式计算所发展出来的概念。云计算和网格计算之间并没有太大的不同，只是网格计算这个名词出现得比较早，它的重点是异构系统之间计算资源的整合。3）网格计算通常只是使用专属的应用协议和数据格式，但云计算没有此限制。云计算则强调在本地资源有限的情况下，用互联网获取云端的计算资源。但网格计算不存在这些情况。总而言之，我们可以用“云计算是平民化的网格计算”来说明它们之间的关系。......
2023-11-18
-
水文分析计算与洪水的时序分期详细阅读
5.9.1.1分析降雨、洪水特性河流洪水年内的季节变化有一定规律，因此，为了合理地选择洪水分期，应首先分析形成洪水的天气条件、降水类型和降雨过程的特点，以及流域产汇流条件等在季节上的差异，年内不同洪峰、洪量值及统计参数的差异，年最大洪水在各季出现的频次，以及不同季节洪水过程线形状有无明显差别等。......
2023-08-23
-
梁的强度与加载方式的影响：计算与分析详细阅读
7-1 求图7-38 所示各梁指定截面上的剪力和弯矩。7-3 如图7-40 所示简支梁，载荷F 可按四种方式作用于梁上，试分别画弯矩图，并从强度方面考虑，指出何种加载方式最好。图7-41题7-4图7-5 如图7-42 所示悬臂梁，横截面为矩形，承受载荷F1 与F2 作用，且F1=2 kN，F2=5 kN，试计算梁内的最大弯曲正应力，及该应力所在截面上K 点处的弯曲正应力。图7-50题7-13图7-14 等刚度的简支梁受力如图7-51 所示。图7-51题7-14图图7-52题7-15图......
2023-06-19
-
生态数据分析与建模：直线回归分析的计算详细阅读
直线回归是回归分析中最简单的一种，又称为简单回归。（一）直线回归方程散点图上呈现直线趋势的两个变数，自变量x的每一个取值都有y的一个分布与之对应。试计算其直线回归方程。为简化手续，可从以下恒等式得出：（五）直线回归的数学模型和基本假定回归分析的依据是直线回归模型。......
2023-11-17
-
河道汇流计算与水文分析详细阅读
河道汇流计算就是利用河段中的蓄泄关系与水量平衡原理把上断面流量过程演算成下断面流量过程，常用河槽汇流曲线进行演算。此汇流曲线用于河道洪水演算的优越性，在于它能考虑演算河段中区间汇入的各支流各自的入流点距下游断面的远近而应受到的不同大小的调节作用。2）华水汇流曲线。......
2023-08-23
-
定位误差的分析与计算方法详细阅读
要解决这一问题，需要进行工件定位误差的分析和计算。如果工件定位误差不超过工件加工尺寸公差值的1/3，一般认为该定位方案能满足本工序加工精度的要求。由于此变化量是由工件的定位而引起的，故称为定位误差，用ΔD 表示。图5-19基准位移引起的定位误差定位误差的来源主要有两个方面。......
2023-06-29
相关推荐