任何一件具体的因果关系都可以用一个逻辑函数描述。例如，图4 - 12所示是一个举重裁判电路，可以用一个逻辑函数描述它的逻辑功能。用卡诺图表示逻辑函数的方法将在下一节专门介绍，本小节只介绍前3种表示方法。......
2023-06-24
探讨典型非线性描述函数
【摘要】：下面计算几种典型非线性特性的描述函数。当非线性环节中不包含储能元件时，其输出的一次谐波分量的幅值和相位差与ω无关，故描述函数只与输入信号幅值A有关。所以3.饱和特性的描述函数当输入为x=Asinωt，且A大于线性区宽度a时，饱和特性的输出波形如图7-13所示。图7-18两个非线性环节串联等效图例7-2 求如图7-19所示两个非线性特性串联后总的描述函数N。表7-1典型非线性特性的描述函数续表
描述函数可以从定义式（7-8）出发求得，一般步骤是：
（1）首先由非线性静特性曲线，画出正弦信号输入作用下的输出波形，并写出输出波形y（t）的数学表达式；
（2）利用傅氏级数求出y（t）的基波分量；
（3）将求得的基波分量代入定义式（7-8），即得N（A）。
下面计算几种典型非线性特性的描述函数。
①理想继电器特性的描述函数
当输入为x（t）=Asinωt时，理想继电器特性的输出波形如图7-11所示。
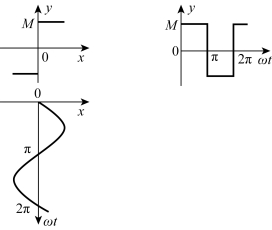
图7-11 理想继电器输入输出波形图
输出y（t）的傅立叶（Fourier）级数形式：
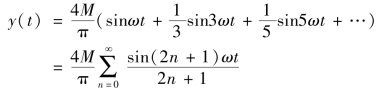
由于输出周期方波信号是奇函数，则傅氏级数中的直流分量与基波偶函数分量的系数为零A0=A1=0，而基波奇函数分量的系数为
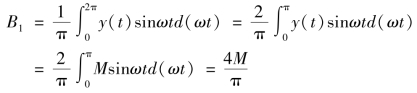
所以，基波分量为
由公式（7-8）得理想继电器特性的描述函数：
即N（A）的相位角为零度，幅值是输入正弦信号A的函数。一般情况下，描述函数是输入信号幅值A和频率ω的函数。当非线性环节中不包含储能元件时，其输出的一次谐波分量的幅值和相位差与ω无关，故描述函数只与输入信号幅值A有关。至于直流分量，若非线性环节的正弦响应为关于t的奇对称函数，即
2.滞环特性的描述函数
当输入为x（t）=Asinωt时，滞环特性的输出波形如图7-12所示。
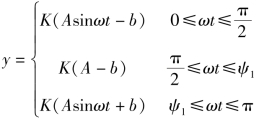
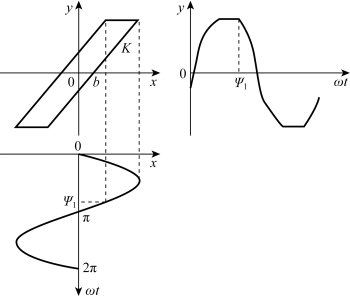
图7-12 滞环特性输入输出波形图
因为y（t）关于原点对称的，则有A0=0。
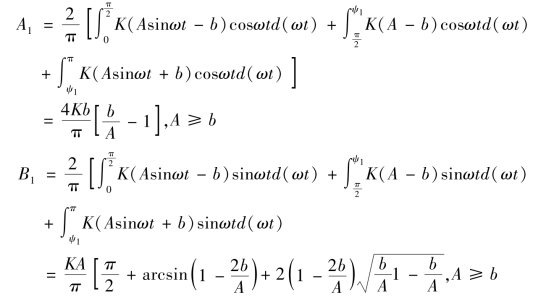
所以
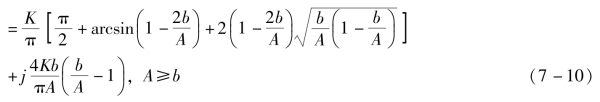
3.饱和特性的描述函数
当输入为x（t）=Asinωt，且A大于线性区宽度a时，饱和特性的输出波形如图7-13所示。
当输入为正弦信号，输出信号为
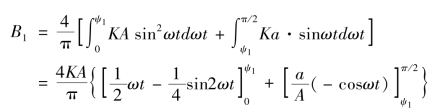
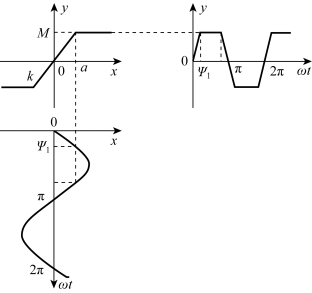
图7-13 饱和非线性特性输入输出波形图
显然其输出信号y（t）是单值奇对称，因此A0=A1=0，而
式中，ψ1=arcsin（a/A）
由公式（7-8）可得饱和特性的描述函数为
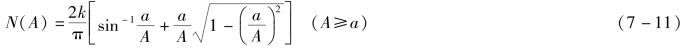
由上式可见，饱和特性的N（A）也是输入正弦信号幅值A的函数。这说明饱和特性等效于一个变系数的比例环节，当A＞a时，比例系数总小于k。
4.继电器特性的描述函数
当输入为x（t）=Asinωt，继电器特性的输出波形如图7-14所示。
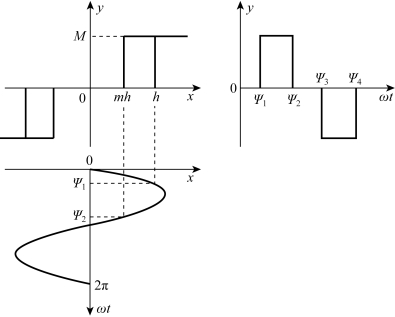
图7-14 继电器特性的输入输出波形图
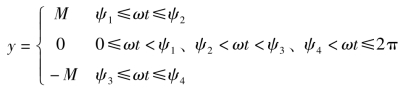
所以y（t）关于原点对称的，则有A0=0，
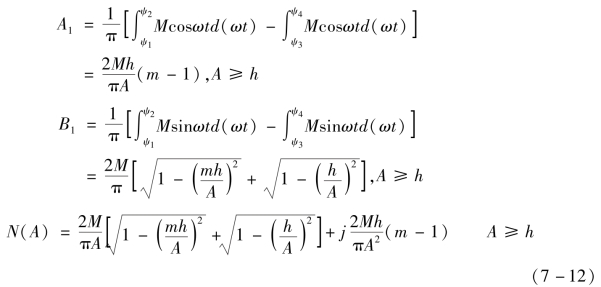
5.组合非线性特性的描述函数
以上介绍了描述函数的基本求法，对于复杂的非线性特性，完全可以利用这种方法求出其描述函数，但计算也复杂得多。此时也可以将复杂的非线性特性分解为若干个简单非线性特性的组合，即串并联，再由已知的这些简单非线性特性的描述函数求出复杂非线性特性的描述函数。
（1）非线性特性的并联计算
设有两个非线性环节并联，且其非线性特性都是单值函数，即它们的描述函数都是实数，如图7-15所示。
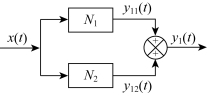
图7-15 两个非线性环节并联
当输入为x（t）=Asinωt时，则两个环节输出的基波分量分别为输入信号乘以各自的描述函数，即
y11(t)=N1Asinωt
y21(t)=N2Asinωt
总输出为
y1(t)=(N1+N2)Asinωt
故总的描述函数为
由此可见，若干个非线性环节并联后的总的描述函数，等于各非线性环节描述函数之和。当N1和N2是复数时，该结论仍成立。
例7-1 图7-16为一个具有死区的非线性环节，求描述函数N（A）。
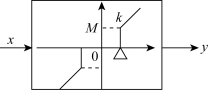
图7-16 例7-1具有死区的非线性特性
解：由图7-17可见，该死区非线性特性可分解为一个死区继电器特性和一个典型死区特性的并联，其描述函数为
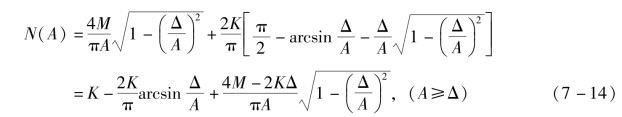
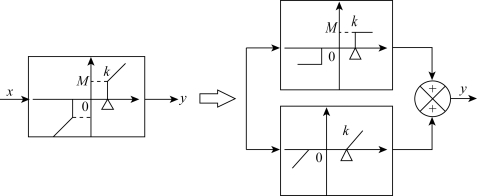
图7-17 例7-1具有死区的非线性特性的并联分解图
（2）非线性特性的串联计算
若两个非线性环节串联，如图7-18所示，其总的描述函数不等于两个非线性环节描述函数的乘积，必须首先求出这两个非线性环节串联后等效的非线性特性，然后根据等效的非线性特性求出总的描述函数。
图7-18 两个非线性环节串联等效图
例7-2 求如图7-19所示两个非线性特性串联后总的描述函数N（A）。
解：这是一个死区特性和一个饱和特性相串联。根据各串联环节输入输出之间的关系，可以等效为一个死区加饱和的非线性特性。
为求得这个等效非线性特性的描述函数，又可将其分解为两个具有完全相同线性区斜率k=2和不同死区宽度死区特性的并联相减，如图7-19所示，故总的描述函数为
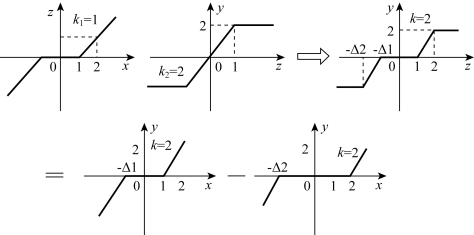
图7-19 例题7-2两个非线性特性串联图
表7-1列出了常见的非线性系统特性及其描述函数N（A），供分析时参考。理想继电特性、死区继电特性、饱和特性、死区特性最好能记住！
表7-1 典型非线性特性的描述函数
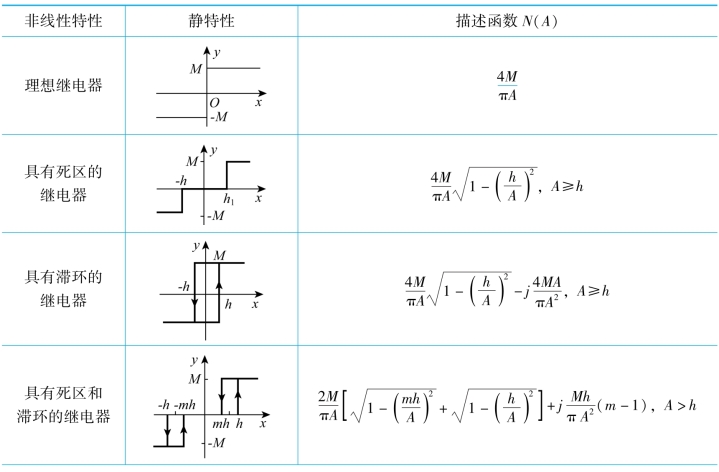
续表
有关自动控制原理的文章
- 详细阅读
-
传递函数示例——典型环节详细阅读
比例环节的表达式为比例环节的传递函数为在物理系统中无弹性变形的杠杆、非线性和时间常数可以忽略不计的电子放大器、传动链之速比以及测速发电机的电压和转速的关系，都可以认为是比例环节。图2-7微分环节如图2-7所示的电路的微分方程为消去中间变量得相应的传递函数为式中，Tc=RC。称具有这种传递函数形式的环节为比例微分环节。一阶惯性环节的微分方程为其传递函数可以写成如下表达式：式中，K——比例系数；T——时间常数。......
2023-06-28
-
描述函数法：基本概念简介详细阅读
能较好地滤除非线性环节在正弦输入下的输出中的高次谐波，于是可以认为在闭环通道中只有基波分量在流通，此时应用描述函数法所得的分析结果才是比较准确的。描述函数类似于线性系统中的频率特性，利用描述函数的概念便可以把一个非线性元件近似地看作一个线性元件，因此又叫作谐波线性化，是线性系统频率法的推广。描述函数表达了非线性元件对基波正弦量的传递能力。......
2023-06-28
- 详细阅读
-
连接功能的数学描述：深入探讨详细阅读
通常交换网络内部的通道被称为“连接”，建立内部通道就是建立连接，拆除内部通道就是拆除连接。下面分别从连接集合和连接函数出发来讨论。连接函数实际上也反映了入线编号构成的数组和出线编号构成的数组之间对应的置换关系或排列关系。所以连接函数也被称为置换函数或排列函数。图4.15连接函数δ=x1x0x2的图形表示......
2023-06-26
-
复变函数及其应用：形如的积分探讨详细阅读
定理3 设函数f(z)在实轴上无奇点,且在上半平面除有限个奇点z1,z2,··· ,zn外解析,若存在正数M和r,使当|z|≥r且Imz ≥0 时,函数f(z)解析且有则有证明 设CR为上半圆周: z = Reiθ(0 ≤θ ≤π),取充分大的R使R ≥r,并且奇点z1,z2,··· ,zn均在由CR 及实轴上从-R到R的一段所围成的半圆内,则由留数定理得只须证明当R →+∞时,上述沿CR 的积分......
2023-10-30
-
拉普拉斯方程的边值问题的典型案例in《复变函详细阅读
实际应用中经常遇到这样的拉普拉斯方程的边值问题一广义狄利克莱(Dirichlet) 问题.即设Γ是有限复平面上单连通域D的边界,又定义函数g(p)在Γ上连续,或至多有有限个第一类间断点.试求在D内有界的调和函数φ(x,y),使对g(p)在Γ上的连续点P满足这类问题中,对于区域D比较简单的情形,有时可直接利用在D内解析函数的实部或虚部都是调和函数来直接得到所求问题的解.但当区域复杂时,我们可通过一个......
2023-10-30
-
典型浅滩整治参数及最佳时机的探讨详细阅读
这是航道整治人员非常关注的问题。根据河床断面关系法，在航道图上选择若干断面并在各断面图上找出相应于整治水位的水位线，并量出这两点的河宽以表示整治水位Z下的河宽B。截至目前，窑监河段的河床调整远未达到平衡，整治线宽度仍在变化中。一般认为，浅滩水深比较大就是有利时机。......
2023-06-21
相关推荐