首页理论教育描述函数法：基本概念简介

描述函数法：基本概念简介

2023-06-28 理论教育版权反馈

【摘要】：能较好地滤除非线性环节在正弦输入下的输出中的高次谐波，于是可以认为在闭环通道中只有基波分量在流通，此时应用描述函数法所得的分析结果才是比较准确的。描述函数类似于线性系统中的频率特性，利用描述函数的概念便可以把一个非线性元件近似地看作一个线性元件，因此又叫作谐波线性化，是线性系统频率法的推广。描述函数表达了非线性元件对基波正弦量的传递能力。

1.描述函数的应用条件

（1）非线性系统的结构图可简化成一个非线性环节N和一个线性部分G（s串联的闭环结构，如图7-10所示。

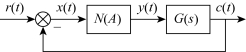
pagenumber_ebook=208,pagenumber_book=197

图7-10　非线性系统的典型结构图

（2）非线性环节的输入输出静特性曲线是奇对称的，即y（x）=-y（-x），以保证非线性元件在正弦信号作用下的输出不包含直流分量。

（3）系统的线性部分具有良好的低通滤波特性。能较好地滤除非线性环节在正弦输入下的输出中的高次谐波，于是可以认为在闭环通道中只有基波分量在流通，此时应用描述函数法所得的分析结果才是比较准确的。

根据上述条件，则输出y（t）用基波分量代替。y（t）基波分量为

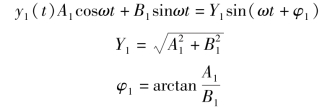
pagenumber_ebook=208,pagenumber_book=197

式中，Y1为基波分量振幅；φ1基波分量相对于输入正弦信号的相移。

以上各式表明：一个非线性环节在正弦信号的输入作用下，其输出也是一个同频率的正弦量，只是振幅和相位发生了变化。这个与线性元件在正弦信号作用下的输出具有形式上的相似性。

2.描述函数的定义

对于如图7-10所示的非线性系统，设系统的非线性环节输入信号是正弦信号：

x(t)=Asinωt

则其输出一般为周期性的非正弦信号，可以展成傅立叶级数为

pagenumber_ebook=208,pagenumber_book=197

式中，

pagenumber_ebook=209,pagenumber_book=198

若系统满足上述第二个条件，则有A0=0。

由于在傅氏级数中n越大，谐波分量的频率越高，An，Bn越小。此时，若系统又满足第三个条件，则高次谐波分量又进一步被充分衰减，故可认为非线性环节的稳态输出只含基波分量，即

y(t)≈y1(t)=A1cosωt+Bsinωt=Y1sin(ωt+φ1)

式中，

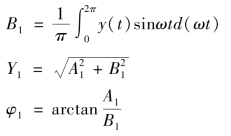
pagenumber_ebook=209,pagenumber_book=198

类似于线性系统中频率特性的定义，我们把非线性元件稳态输出的基波分量与输入正弦信号的复数比定义为非线性特性的描述函数，用N（A）来表示，即

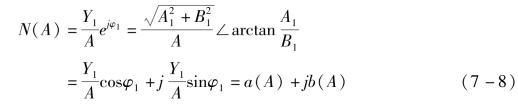
pagenumber_ebook=209,pagenumber_book=198

由非线性环节描述函数的定义可以看出如下内容。

（1）描述函数类似于线性系统中的频率特性，利用描述函数的概念便可以把一个非线性元件近似地看作一个线性元件，因此又叫作谐波线性化，是线性系统频率法的推广。

（2）描述函数表达了非线性元件对基波正弦量的传递能力。一般来说，它应该是输入信号幅值和频率的函数，但对于绝大多数的实际非线性元件，由于不包括储能元件，它们输出与输入频率无关，但是幅值函数，故常用N（A）表示。