方法验证是实验室针对标准方法或官方发布的方法的验证。如果只是对标准方法稍加修改，如使用不同制造商的同类设备或试剂等，必要时也应进行验证，以证明能够获得满意的结果，并将其修改内容制订成作业指导书文件。根据《GB/T 27417—2017合格评定 化学分析方法确认和验证指南》的规定，典型的需要验证的方法特性参数如表2－17所示［4］。......
2023-06-29
控制系统典型的非线性特性优化方案
【摘要】：饱和特性在控制系统中是普遍存在的，常见的调节器就具有饱和非线性。上述介绍的是一些典型非线性特性。
控制系统中的非线性特性按照其物理特性及非线性特性的形状划分为饱和非线性、死区（不灵敏区）非线性、具有不灵敏区的饱和非线性、继电非线性、间隙非线性等。
1.饱和非线性
饱和非线性又称饱和特性，其静特性曲线如图7-2所示，其数学表达式为式（7-1）。
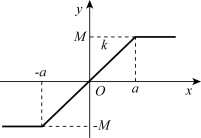
图7-2 饱和非线性特性
式（7-1）中，a为线性区宽度，k为线性区斜率。饱和非线性的特点是：输入信号超过某一范围后，输出不再随输入的变化而变化，而是保持在某一常值上。饱和特性在控制系统中是普遍存在的，常见的调节器就具有饱和非线性。饱和特性对系统性能的影响是使系统在大信号作用下开环增益下降，因而降低了稳态精度。
2.死区（不灵敏区）非线性
死区又称不灵敏区，在死区内虽有输入信号，但其输出为零。死区特性常常是由放大器、传感器、执行机构的不灵敏区造成的。其静特性关系如图7-3所示，理想型死区特性的数学表达式为式（7-2）。
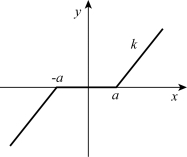
图7-3 死区（不灵敏区）非线性
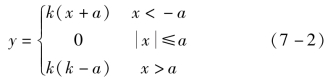
死区特性常见于许多控制设备与控制装置中，如各种测量元件的不灵敏区，在死区内虽有输入信号，但其输出为零。当死区很小，如果对系统的性能不会产生不良影响时，可以忽略不计，否则，必须将死区特性考虑进去。死区非线性特性对系统性能的影响是导致系统产生稳态误差，且用提高增量的方法也无法消除。在工程实践中，为了提高系统的抗干扰能力，有时又故意引入或增大死区。
3.具有不灵敏区的饱和非线性
在不少情况下，系统的元件同时存在死区特性和饱和特性。例如，测量元件的测量值规定在一个范围内的，即不能太小也不能太大；电枢电压控制的直流电动机带恒转矩及空气摩擦性负载时的控制特性是既有不灵敏特性又有饱和特性的非线性。具有不灵敏区的饱和非线性如图7-4所示，具有不灵敏区的饱和非线性的数学表达式为式（7-3）。
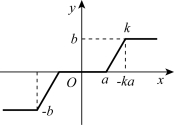
图7-4 具有不灵敏区的饱和特性
4.滞环特性
滞环特性表现为正向与反向特性不是重叠在一起，而是在输入输出曲线上出现闭合环路，其静特性曲线如图7-5所示，其数学表达式为式（7-4）。
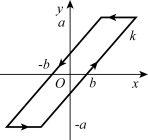
图7-5 滞环特性
式（7-4）中signx为符号函数，当x＞a，signx=1；当x＜-a，signx=-1。滞环特性的特点是：当输入信号小于间隙b时，输出为零。当x＞b时，输出随输入线性变化；输入反向时，输出保持在方向发生变化时的输出值上，直到输入反向变化2a后，再线性变化。例如，铁磁材料的磁滞现象、齿轮传动中的齿隙、液压传动中的间隙等均属于这类特性。间隙特性对系统性能的影响是间隙使输出相位滞后，减小稳定性裕量，动态特性变坏。
5.继电器特性
分析继电特性有十分重要的意义，因为采用继电器、电磁阀等元件的控制系统比比皆是，如大多数家用电冰箱、空调就是继电器控制系统。由于继电器吸合及释放状态下磁路的磁阻不同，继电器的吸合与释放的电流不相同，因此继电器的特性有滞环。具有死区和滞环的三位置继电特性如图7-6所示，其数学表达式为式（7-5）。带死区的继电特性，将会增加系统的定位误差，对其他动态性能的影响，类似于死区、饱和非线性特性的综合效果。
图7-6 具有滞环的三位置继电特性
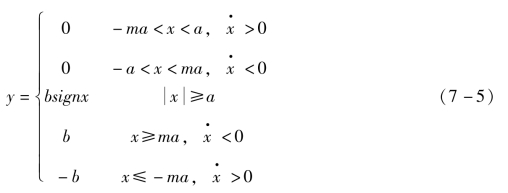
继电器特性还有如下三种特殊情况。
（1）若a=0，称这种特性为理想继电器特性，如图7-7（a）所示。
（2）若m=1，其静特性如图7-7（b）所示，则称为死区继电器特性。
（3）若m=-1，则称为滞环继电器特性，如图7-7（c）所示。
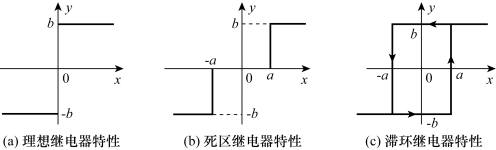
图7-7 三种继电器特性
6.间隙（回环）非线性
间隙非线性也称为回环非线性，如图7-8所示，图中x为输入量，y为输出量，b为间隙值，齿轮之间有少量的间隙保证了齿轮在传动中转动灵活不发生卡死现象，这样当机构做反向运动时，主动齿轮总是要转过间隙内的空行程后才能推动从动齿轮转动。其特点是：当输入量的方向改变时，输出量保持不变，一直到输入量的变化范围超出一定数值（间隙）后，输出量才变化。传动机构的间隙也是控制系统中常见的非线性特性，齿轮传动是典型的间隙特性。设齿轮传动速比为c，则间隙特性的数学表达式为式（7-6）。式中，b为常数，它等于主动轮改变方向时的值。间隙特性类似于线性系统的滞后环节，但不完全等价，它对控制系统的动态、稳态特性都不利。
图7-8 间隙（回环）非线性
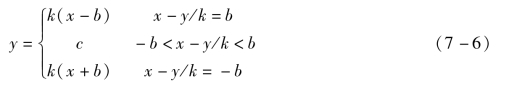
7.变增益特性
变增益特性的静特性曲线如图7-9所示，其数学表达式为式（7-7）。
图7-9 变增益特性
式（7-7）中k1，k2为变增益特性的斜率，a为转换点，变增益特性使系统在大误差信号时具有较大的增益，从而使系统响应迅速；而在小误差信号时具有较小的增益，从而提高系统的相对稳定性。同时抑制高频低振幅噪声，提高系统响应控制信号的准确度。
上述介绍的是一些典型非线性特性。实际中的非线性还有好多复杂的情况，有些是它们的组合，还有一些很难用一般的函数来描述，可以称为不规则非线性。
有关自动控制原理的文章
- 详细阅读
-
典型机床夹具优化方案详细阅读
图2-21 十字槽轮精车工序简图图2-22 花盘式车床夹具1，3，4—定位套 2—定位销1）mm圆弧尺寸由刀具调整来保证。3）夹具体上φ120mm止口与过渡盘上φ120mm凸台采用过盈配合，设计要求就地加工过渡盘端面及凸台，以减小夹具的对刀和定位误差。工件的装夹就是将工件在机床上或夹具中定位、夹紧的过程。图2-23 角铁式车床夹具2）在自定心卡盘上装夹工件。图2-24所示为立式铣床铣轴承座底面的夹具。......
2023-06-26
-
典型LED的选配应用优化方案详细阅读
图3-14 SDL-109C系列控制器通用型控制器连接方式简单，与LED变色管一起使用时可以产生丰富多彩的效果。该控制器配合3060功率放大器使用，每增加一个功率扩展器可多连接1倍数量的LED，可实现输出功率的无限放大。图3-18 LED七彩控制器电气特性：RS-485、RS-422使用RJ45接口。......
2023-06-15
-
控制系统优化方案：PLC技术的高效控制系统详细阅读
使用PLC构成控制系统，与同等规模的继电接触器系统相比，电气接线及开关接点已减少很多，故障也就大大降低。PLC的输入可直接与交流110V、直流24V等信号相连接，输出可直接驱动交流220V、直流24V的负载，无须再进行电平转换与光电隔离，因而可以方便地构成各种控制系统。......
2023-07-01
-
探讨典型非线性描述函数详细阅读
下面计算几种典型非线性特性的描述函数。当非线性环节中不包含储能元件时，其输出的一次谐波分量的幅值和相位差与ω无关，故描述函数只与输入信号幅值A有关。所以3.饱和特性的描述函数当输入为x=Asinωt，且A大于线性区宽度a时，饱和特性的输出波形如图7-13所示。图7-18两个非线性环节串联等效图例7-2 求如图7-19所示两个非线性特性串联后总的描述函数N。表7-1典型非线性特性的描述函数续表......
2023-06-28
-
典型材料搅拌摩擦焊的优化方案详细阅读
当以这个区间内的参数进行搅拌摩擦焊时，可以获得最佳性能的搅拌摩擦焊接头。这说明，焊核区晶粒在搅拌摩擦焊中发生了再结晶而得到了细化。与铝合金搅拌摩擦焊的焊接接头微观组织相比，钛合金搅拌摩擦焊接头明显没有热机影响区。接头的拉伸性能测试结果表明，搅拌摩擦焊接头的力学性能优于TIG焊，并且与母材性能很接近，当母材的增强相分布不均匀时，搅拌摩擦焊接头的强度比母材高。......
2023-06-26
- 详细阅读
-
位置伺服控制系统优化方案详细阅读
伺服控制系统是一种能够跟随输入指令信号进行控制的系统，也称随动控制系统。位置伺服控制系统用于机械的定位和定向控制，机器人、数控机床、雷达跟踪、舰船操舵等都大量使用电动机控制的位置伺服系统。位置闭环控制与调速系统的不同是其有位置检测和位置控制器。本章主要介绍步进电动机位置开环控制原理和伺服电动机位置闭环控制系统的组成和控制要求。......
2023-06-19
相关推荐