取滞后部分第二个转折频率为则有，则T2=100，由此可得，滞后—超前校正装置的传递函数为其伯德图，如图6-11中Lc和φc所示。图6-11例6-3系统串联滞后—超前校正伯德图......
2023-06-28
MATLAB实现滞后-超前校正技术
【摘要】：当待校正系统不稳定，且要求校正后系统的响应速度、相角裕量和稳态精度较高时，采用滞后—超前校正为宜。其基本原理是利用滞后超前网络的超前部分来改善系统的相角裕量，同时利用滞后部分来改善系统的稳态性质。下面举例说明使用Matlab进行滞后—超前校正的设计步骤。运行程序，可以得到超前装置、滞后校正装置和校正后系统的传递函数分别如下：校正后的相角裕量为48.1°，幅值裕度为10.2dB，校正后的Bode图如图6-25所示。图6-25校正后系统的Bode图
滞后—超前校正兼有滞后校正和超前校正的优点，即校正系统响应速度较快，超调量较小，抑制高频噪声的性能也较好。当待校正系统不稳定，且要求校正后系统的响应速度、相角裕量和稳态精度较高时，采用滞后—超前校正为宜。其基本原理是利用滞后超前网络的超前部分来改善系统的相角裕量，同时利用滞后部分来改善系统的稳态性质。下面举例说明使用Matlab进行滞后—超前校正的设计步骤。
例6-7 已知某系统的开环传递函数为
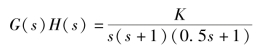
要求设计校正装置，使系统满足：
（1）Kv=5s-1时；
（2）相角裕量为γ≥45°。
解：步骤如下。
（1）确定开环增益。由题意，可选取系统的开环增益K=5。
（2）画出未校正系统的Bode图，并标明各频域性能指标。
程序代码如下：
运行程序，可以得到未校正系统的Bode图，如图6-24所示。
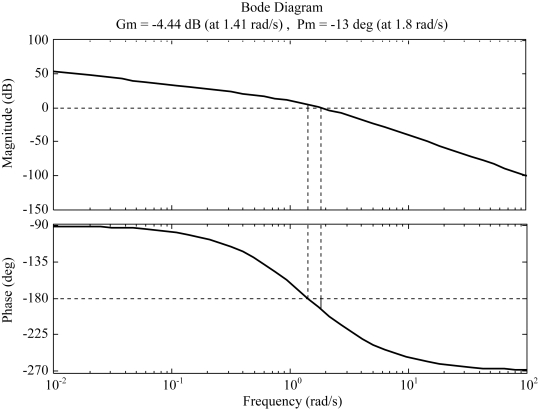
图6-24 未校正系统的Bode图
由未校正系统的Bode图可知，未校正系统的相位穿越频率为1.41rad/s，对应的幅值裕度为-4.44dB，剪切频率为1.8rad/s，对应的相角裕度为-13°，可知不满足性能指标要求，并且系统不稳定。由于未校正系统在剪切频率处的相角滞后远小于180°，且对响应速度有要求，因此采用串联滞后—超前校正。根据其设计步骤，编写如下程序。
运行程序，可以得到超前装置、滞后校正装置和校正后系统的传递函数分别如下：
校正后的相角裕量为48.1°，幅值裕度为10.2dB，校正后的Bode图如图6-25所示。
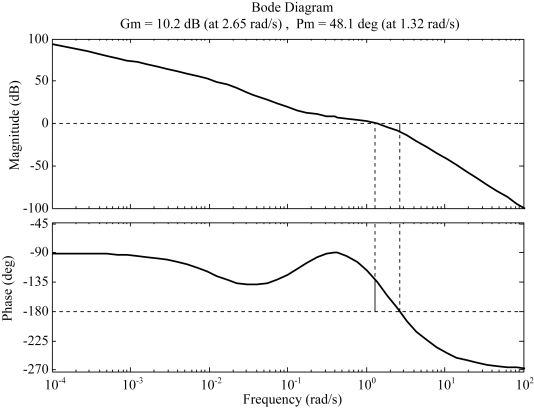
图6-25 校正后系统的Bode图
有关自动控制原理的文章
- 详细阅读
-
使用MATLAB进行超前校正方法优化详细阅读
由于超前校正环节相频特性曲线具有正的相角，幅频特性具有正的斜率，所以校正后系统Bode图的低频不变，而其剪切频率和相角裕量比原系统的大，这说明校正后系统的快速性和稳定性得到了提高。下面举例说明使用MATLAB对系统进行超前校正的设计步骤。根据稳态误差的要求调整K的值。画出未矫正系统的Bode图，校验性能指标是否满足要求。由图6-22可以看出，校正后系统的剪切频率和相角裕量满足了设计的要求。图6-22超前校正前、后系统的Bode图......
2023-06-28
-
滞后-超前校正的优化：方法和意义详细阅读
滞后-超前校正环节的传递函数为：滞后-超前校正环节的伯德图如图12-12所示。低频段具有负的斜率和负的相位差，起滞后校正作用。图12-12 滞后-超前校正环节的伯德图图12-13 原系统的开环伯德图1.校正原理低频部分利用校正环节的滞后部分以改善系统的稳态精度。由此即可确定总的滞后-超前校正环节。......
2023-06-15
-
相位超前校正技术简介详细阅读
图6-3相位超前校正装置伯德图图6-4是一个无源相位超前校正网络的电路图。由图求出原系统截止频率ωc0=3.5rad/s，相位裕量γ0=16°＜γ*，可考虑采用超前校正。在有些情况下，串联超前校正的应用会受到限制。这是因为校正后系统的截止频率会向高频段移动，在新的截止频率处，由于未校正系统的相位滞后量过大，所以用单级超前校正网络难以获得所要求的相位裕量。......
2023-06-28
-
微分（超前）校正方法详解详细阅读
微分（超前）校正环节的数学模型为，其伯德图如图12-11所示。图12-11 微分校正环节的伯德图1.校正原理使校正环节的两个转折频率［1/T和1/（αT）］分别位于原系统剪切频率ωc的两侧，则校正后系统的幅频曲线在ωc附近的那一段将上移，幅值裕量将增加。......
2023-06-15
-
积分校正滞后环节优化详细阅读
图12-10 积分校正环节的伯德图积分校正环节的数学模型为，其伯德图如图12-10所示。积分校正环节的参数选择也基于上述原理。6）滞后环节的另一较小的交接频率。......
2023-06-15
-
线性系统超前校正设计策略详细阅读
图6-47未校正系统输出显示与测量结果图6116 添加“渐变叠加”图层样式图6-48校正后系统输出显示与测量结果从图6-47、图6-48输出结果可知,基于所设计软件的输出结果与上述仿真、实验结果基本一致,验证了软件功能的有效性。校正后线性系统的时域性能指标提取程序设计方法与上述6.3中相同,请扫描6.3节二维码获取。......
2023-06-21
-
相位滞后校正：解决信号不同步问题详细阅读
由图可见，相位滞后装置在频率之间呈积分效应，对数相频特性呈滞后特性，故称为相位滞后校正装置。同样，可计算出最大滞后频率最大滞后角图6-6相位滞后装置的伯德图由图6-6可见，滞后校正装置在低频时的幅值为0dB，高频时幅值为20lgβ，是负值。所以，滞后校正以减小截止频率来换取相位裕量的提高。而且，只有那些原系统的低频段具有满足性能要求的相位储备的系统才能采用滞后校正。......
2023-06-28
相关推荐