由于超前校正环节相频特性曲线具有正的相角，幅频特性具有正的斜率，所以校正后系统Bode图的低频不变，而其剪切频率和相角裕量比原系统的大，这说明校正后系统的快速性和稳定性得到了提高。下面举例说明使用MATLAB对系统进行超前校正的设计步骤。根据稳态误差的要求调整K的值。画出未矫正系统的Bode图，校验性能指标是否满足要求。由图6-22可以看出，校正后系统的剪切频率和相角裕量满足了设计的要求。图6-22超前校正前、后系统的Bode图......
2023-06-28
相位滞后与超前校正优化方法
【摘要】：取滞后部分第二个转折频率为则有，则T2=100，由此可得，滞后—超前校正装置的传递函数为其伯德图，如图6-11中Lc和φc所示。图6-11例6-3系统串联滞后—超前校正伯德图
当系统的稳态性能与动态性能都不能满足要求，用单一的超前校正或滞后校正无法同时改善系统的稳态和动态性能时，就应该考虑采用相位滞后—超前校正。
1.相位滞后—超前装置及其特性
滞后—超前校正网络的传递函数为
式中，
为超前部分，
为滞后部分。
滞后—超前装置的伯德图，如图6-9所示。可见，低频段部分是滞后校正，高频段部分是超前校正。
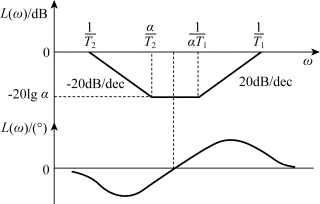
图6-9 滞后—超前装置的伯德图
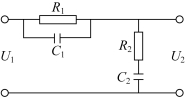
图6-10 无源滞后—超前网络
滞后—超前装置可用如图6-10所示的无源网络来实现，其中αT1=R1C1，βT2=R2C2，T1+T2=R1C1+R2C2+R1C2，且αβ=1，T1＜T2。
2.串联滞后—超前校正设计
滞后—超前校正的设计，实际上是前面所述滞后校正和超前校正的设计方法的综合。滞后—超前校正的本质是利用校正装置中超前部分的相位超前角来增大系统的相位裕量，以改善系统的动态性能；利用滞后部分幅值衰减，允许系统低频段的增益提高，以改善系统的稳态精度。
滞后—超前校正装置的设计步骤如下。
（1）根据稳态误差或静态误差系数的要求确定系统的开环增益K，并绘制原系统的开环伯德图，计算频域性能指标ωc0和γ0。
（2）根据要求的相位裕量γ*或幅值穿越频率ωc*，设计超前校正部分的转折频率
和
（3）确定滞后部分的转折频率
和
。为了使滞后校正部分的相位滞后尽量不影响相位裕量，一般按
的原则取值。
（4）绘制较正后系统的伯德图，校验全部性能指标是否满足要求，如不满足，应重新进行滞后部分的计算，必要时应重新进行全部校正的计算，直至全部性能指标都得到满足为止。
例6-3 设未校正系统的开环传递函数为
设计校正装置，使系统满足Kv=10s-1，γ*≥50°，ω*c≥1.2rad/s，h*≥10dB。
解：（1）确定开环增益K，并绘制原系统伯德图。
由题意，可得
K=Kv=10s-1
原系统的伯德图，如图6-11中L0和φ0所示。由图计算出幅值穿越频率ωc0=2.7rad/s，相位裕量γ0=-33°，相位穿越频率ωg0=1.41rad/s，幅值裕量h0=-14dB，表明原系统不稳定。
（2）确定超前部分。
考虑到ω*c≥1.2rad/s的设计要求，且φ0（1.41）=-180°，可选取ωc=1.5rad/s，超前部分应提供的超前相角为
φm=γ*+Δ=50°+10°=60°
则有
在原系统特性中L0（ωc）=20lg10-40lgωc=13dB，为了使校正后特性在ωc=1.5rad/s处穿越0dB线，必须有Lc（ωc）=-13dB。过Lc（ωc）=-13dB作斜率为+20dB/dec的直线，直线与0dB交点即为转折频率1/T1。由图6-11可得
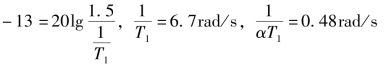
则有T1=0.15，αT1=2.08。
（3）确定滞后部分。
取滞后部分第二个转折频率为
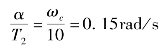
则有
，则T2=100，
由此可得，滞后—超前校正装置的传递函数为
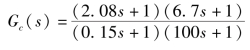
其伯德图，如图6-11中Lc和φc所示。
（4）绘制校正后系统伯德图并检验结果。
校正后系统的传递函数为
校正后系统伯德图如图6-11中L和φ所示。校正后系统性能指标γ=51°，ωc=1.5rad/s，h=14.5dB，Kv=10s-1，满足设计要求。
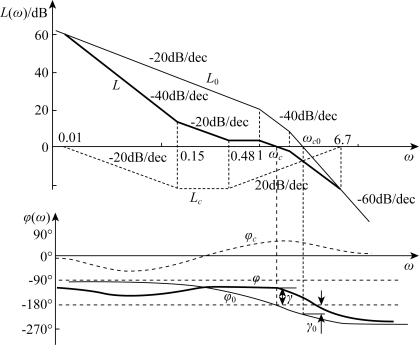
图6-11 例6-3系统串联滞后—超前校正伯德图
有关自动控制原理的文章
- 详细阅读
-
滞后-超前校正的优化：方法和意义详细阅读
滞后-超前校正环节的传递函数为：滞后-超前校正环节的伯德图如图12-12所示。低频段具有负的斜率和负的相位差，起滞后校正作用。图12-12 滞后-超前校正环节的伯德图图12-13 原系统的开环伯德图1.校正原理低频部分利用校正环节的滞后部分以改善系统的稳态精度。由此即可确定总的滞后-超前校正环节。......
2023-06-15
-
微分（超前）校正方法详解详细阅读
微分（超前）校正环节的数学模型为，其伯德图如图12-11所示。图12-11 微分校正环节的伯德图1.校正原理使校正环节的两个转折频率［1/T和1/（αT）］分别位于原系统剪切频率ωc的两侧，则校正后系统的幅频曲线在ωc附近的那一段将上移，幅值裕量将增加。......
2023-06-15
-
相位超前校正技术简介详细阅读
图6-3相位超前校正装置伯德图图6-4是一个无源相位超前校正网络的电路图。由图求出原系统截止频率ωc0=3.5rad/s，相位裕量γ0=16°＜γ*，可考虑采用超前校正。在有些情况下，串联超前校正的应用会受到限制。这是因为校正后系统的截止频率会向高频段移动，在新的截止频率处，由于未校正系统的相位滞后量过大，所以用单级超前校正网络难以获得所要求的相位裕量。......
2023-06-28
-
MATLAB实现滞后-超前校正技术详细阅读
当待校正系统不稳定，且要求校正后系统的响应速度、相角裕量和稳态精度较高时，采用滞后—超前校正为宜。其基本原理是利用滞后超前网络的超前部分来改善系统的相角裕量，同时利用滞后部分来改善系统的稳态性质。下面举例说明使用Matlab进行滞后—超前校正的设计步骤。运行程序，可以得到超前装置、滞后校正装置和校正后系统的传递函数分别如下：校正后的相角裕量为48.1°，幅值裕度为10.2dB，校正后的Bode图如图6-25所示。图6-25校正后系统的Bode图......
2023-06-28
-
线性系统超前校正设计策略详细阅读
图6-47未校正系统输出显示与测量结果图6116 添加“渐变叠加”图层样式图6-48校正后系统输出显示与测量结果从图6-47、图6-48输出结果可知,基于所设计软件的输出结果与上述仿真、实验结果基本一致,验证了软件功能的有效性。校正后线性系统的时域性能指标提取程序设计方法与上述6.3中相同,请扫描6.3节二维码获取。......
2023-06-21
-
相位滞后校正：解决信号不同步问题详细阅读
由图可见，相位滞后装置在频率之间呈积分效应，对数相频特性呈滞后特性，故称为相位滞后校正装置。同样，可计算出最大滞后频率最大滞后角图6-6相位滞后装置的伯德图由图6-6可见，滞后校正装置在低频时的幅值为0dB，高频时幅值为20lgβ，是负值。所以，滞后校正以减小截止频率来换取相位裕量的提高。而且，只有那些原系统的低频段具有满足性能要求的相位储备的系统才能采用滞后校正。......
2023-06-28
-
复合校正中按扰动补偿的优化方法详细阅读
图6-20按扰动补偿的复合控制系统引入扰动补偿后，扰动作用下的误差为显然，选择前馈补偿装置的传递函数为这时有En=0，即扰动对系统的输出和误差无影响。但是，由于物理系统传递函数的分母阶数总是大于分子的阶数，按式、式实现误差全补偿的条件在物理上往往无法准确实现。图6-21例6-4复合控制系统结构图解：由式有输入，所以有要使esr=0，Gc的最简式应为可见，引入信号微分作为前馈补偿后，完全消除了斜坡信号作用下的稳态误差。......
2023-06-28
相关推荐