相位超前校正技术简介

2025-09-29 理论教育版权反馈

【摘要】：图6-3相位超前校正装置伯德图图6-4是一个无源相位超前校正网络的电路图。由图求出原系统截止频率ωc0=3.5rad/s，相位裕量γ0=16°＜γ*，可考虑采用超前校正。在有些情况下，串联超前校正的应用会受到限制。这是因为校正后系统的截止频率会向高频段移动，在新的截止频率处，由于未校正系统的相位滞后量过大，所以用单级超前校正网络难以获得所要求的相位裕量。

1.相位超前装置及其特性

相位超前装置的传递函数为

根据式（6-1）相位超前装置的伯德图如图6-3所示。由伯德图看出，在频率之间有明显的微分作用，即PD控制。在上述频率范围内，随ω的增大，相位角从0°开始先增后减，输出信号相位角总是超前于输入信号相位角，且在其中心有最大的相位超前角，故称为相位超前装置。超前装置Gc（s）的相频特性为

令，可求得最大相位超前角频率为

pagenumber_ebook=177,pagenumber_book=166

将式（6-3）代入式（6-2）得最大超前角

式（6-4）表明，最大超前角φm仅与α值有关。α值选得越大，则超前校正的微分效应越强。为了保持较高的信噪比，实际选用的α值一般不大20。由图6-3，可以求出ωm处的对数幅频。

由式（6-4），可推出

pagenumber_ebook=177,pagenumber_book=166

利用式（6-6）可以根据所需要的φm确定满足条件的α。

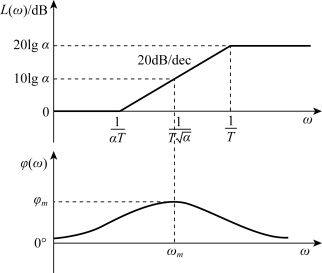
pagenumber_ebook=178,pagenumber_book=167

图6-3　相位超前校正装置伯德图

图6-4是一个无源相位超前校正网络的电路图。

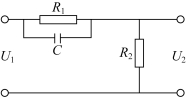
pagenumber_ebook=178,pagenumber_book=167

图6-4　无源相位超前校正网络

设输入信号源内阻为零，输出端负载阻抗无穷大，其传递函数为

式中，

由式（6-7）可看出，若将无源相位超前网络串入系统后，系统开环增益将下降到原来的1/α。为补偿无源超前网络造成的增益衰减，需要另外串联一个放大器将原放大器的放大倍数提高α倍。

2.串联超前校正设计

串联超前校正设计的基本原理：利用超前装置的相位超前特性，为了获得最大的相位超前量，应使最大相位超前角φm叠加在校正后系统的幅值穿越频率（截止频率）处，即ωm=ωc，使校正后系统的相位裕量得到提高，从而改善系统的暂态性能。

设原系统的开环传递函数为G0（s），要求的稳态误差、截止频率、相位裕量和幅值裕量指标分别表示为ess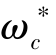， pagenumber_ebook=178,pagenumber_book=167 ，γ和h，设计超前校正的一般步骤可归纳如下。

（1）根据性能指标对稳态误差的要求，确定开环增益K。

（2）由确定的开环增益K绘制原系统的开环伯德图，求出原系统的截止频率ωc0和相位裕量γ0，当ωc0＜ pagenumber_ebook=178,pagenumber_book=167 ，γ0＜γ时，首先考虑使用超前校正。

（3）按照系统要求的相位裕量γ，确定校正装置所应提供的最大相角超前量φm，即

式中，补偿角（5°～15°）是为了补偿因校正后截止频率增大而引起的γ0损失。若原系统的对数幅频特性在截止频率处的斜率为-40dB/dec，并不再向下转折时，补偿角可取为（5°～8°）；若该频段斜率从-40dB/dec继续转折为-60dB/dec，甚至更小时，则补偿角应适当取大些。注意，如果φm＞60°，则一级超前校正不能达到要求的γ指标。

（4）按式（6-6）计算超前校正装置的参数α。

（5）选定校正后系统的截止频率ωc。在原系统的L0（ω）中找出幅频值为-10lgα所对应的角频率，以该频率作为校正后系统的截止频率ωc，即ωm。值得注意的是，若该频率小于性能指标要求的 pagenumber_ebook=179,pagenumber_book=168 ，校正后系统的截止频率可取为ωm==ωc，并以L0（）=-10lgα重新修正α值。

（6）确定校正装置的参数。根据选定的ωm和α，由式（6-3）确定校正装置的参数T：

pagenumber_ebook=179,pagenumber_book=168

此时超前网络的两个转折频率分别为1/T和1/αT。

（7）画出校正后系统的伯德图，校验全部性能指标是否满足要求。若不满足，必须适当增加相角补偿量，从第（3）开始重新设计直到满足要求。当通过调整相角补偿量不能达到设计指标时，应改变校正方案。(https://www.chuimin.cn)

例6-1 设原反馈系统的开环传递函数为，试设计校正装置Gc（s），使校正后系统满足指标：静态速度误差系数Kv=12s-1，开环截止频率ωc≥6rad/s，相位裕量γ≥60°，幅值裕量h≥10dB。

解：

（1）根据静态误差系数的要求，确定开环增益K。

（2）绘制原系统的开环伯德图，如图6-5中L0和φ0所示。由图求出原系统截止频率ωc0=3.5rad/s，相位裕量γ0=16°＜γ，可考虑采用超前校正。

（3）确定需要增加的相位超前角φm。

φm=γ-γ0+6°=60°-16°+6°=50°

（4）确定α值。

（5）确定校正后截止频率ωc。

确定原系统对数幅频特性L0（ω）=-10lgα对应的频率为校正后截止频率ωc。在原系统特性中，有

解得ωc=ωm=5.8rad/s。

考虑到ωc不符合本系统要求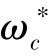 pagenumber_ebook=179,pagenumber_book=168 ≥6rad/s，取ωc=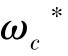=6rad/s，并对α值进行调整。由

解得调整后的校正装置α=8.63。

（6）确定校正装置传递函数。

由式（6-9）得

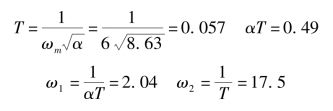
pagenumber_ebook=180,pagenumber_book=169

超前校正装置的传递函数

（7）画出校正后系统的伯德图，校验性能指标。

校正后系统的开环传递函数为

校正网络及校正后系统的伯德图，如图6-5中Lc、φc和L、φ所示。

校正后系统的截止频率ωc=ωc=6rad/s，相位裕量为

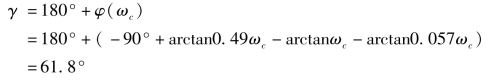
pagenumber_ebook=180,pagenumber_book=169

幅值裕量h→∞＞10dB。满足设计要求。

由图6-5可见，校正前L0（ω）曲线以-40dB/dec斜率穿0dB线，相位裕量不足，校正后L（ω）曲线以-20dB/dec斜率穿过0dB线，并且在ωc=6rad/s附近保持了较宽的频段，相位裕量有了明显的增加。

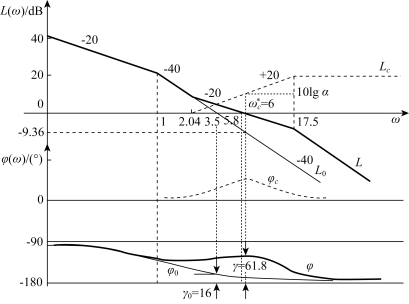
pagenumber_ebook=180,pagenumber_book=169

图6-5　例6-1串联校正系统的伯德图

3.串联超前校正的特点

从以上的分析设计中可归纳出串联超前校正的特点。

（1）超前校正利用超前校正装置的超前相位来提高系统的相位裕量，从而减小了系统响应的超调量，提高了系统的相对稳定性。

（2）超前校正使幅值穿越频率ωc增大，增加了系统的带宽，使系统的响应速度加快。

（3）超前校正网络是一个高通滤波器，校正后使系统的高频段幅值提高了20lgα，使系统抑制高频噪声干扰的能力减弱，这是对系统不利的一面。通常，为了使系统保持较高的信噪比，一般取α=5～20，即用超前校正补偿的相角一般不超过60°。

在有些情况下，串联超前校正的应用会受到限制。例如，若原系统的相频特性曲线在截止频率ωc附近急剧下降时，或者说相角φ（ω）在ωc附近低于-180°太多，采用串联超前校正的效果不大。这是因为校正后系统的截止频率会向高频段移动，在新的截止频率处，由于未校正系统的相位滞后量过大，所以用单级超前校正网络难以获得所要求的相位裕量。此时，可以考虑由两级或者三级超前网络构成校正装置或采用其他校正方法。

相位超前校正技术简介

相关推荐