对于混合物来说，各个晶相的衍射花样会同时出现，而不会出现干涉。X射线物相分析可以鉴别样品中的物相，包括纯元素（单质）、化合物和固溶体。同一种材料，可以具有不同的物相，称为同分异构体。就广义而言，物相衍射分析包括物相鉴定、定量分析、相结构的测定以及相变过程检测等。但对于纳米材料，晶粒的小尺寸会导致衍射峰的宽化，进而影响积分强度的计算，所以纳米材料定量分析的精度和准确度都远低于传统材料。......
2023-06-20
相对稳定性分析方法与应用
【摘要】：确定闭环系统的稳定性。例5-15 系统开环传递函数确定k=0.5、1、1.5、1.6时，闭环系统的稳态性能和暂态性能。闭环系统的稳定性可通过阶跃响应曲线加以验证。与上述结论一致。稳态特性分析例5-15中系统为Ⅰ型系统，则在阶跃输入信号下，稳态误差为零。暂态特性分析对稳定的系统，即K=0.5和K=1时，在伯德图中ωc1＜ωc2则有闭环系统的响应速度减慢，快速性变差。
MATLAB命令为[Gm，Pm，Wcg，Wcp]=margin（sys）
该命令计算系统的增益裕量和相位裕量，以及幅值穿越频率和相角穿越频率。当缺省输出量时，在当前窗口绘制系统的伯德图，并标出相位裕量和增益裕量，以及相角穿越频率和幅值穿越频率。
MATLAB提供的函数都允许用户选择特性分析功能，例如，在系统的伯德图上，若右击鼠标则得出快捷菜单；在Characteristics菜单项中可以选择稳定性相关的菜单项，可以得到对系统频域分析的关键点。其他的函数，如nyquist（）和nichols（），都支持自己的Characteristics菜单选择。
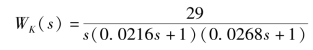
（1）绘制bode图、nyquist图及nichols图。
（2）在各图中，标出系统的增益裕量和相位裕量。
（3）确定闭环系统的稳定性。
解：MATLAB程序：
在MATLAB仿真结果的系统奈氏图（如图5-67所示）上，当ω从-∞到+∞时，奈氏曲线没有包围（-l，j0）点，原开环系统为最小相位系统，则闭环系统稳定。
稳定性也可以根据稳定裕量判别，单击鼠标右键，在选项“characteristics”中选择“stability（MinimumCrossing）”，可得到辅助单位圆，以及相位裕量和增益裕量的点。在伯德图和尼柯尔斯图中也可以很容易地读出相位裕量和增益裕量的数值，得到γ（ωc）=33.23°，GM=9.19dB，则闭环系统稳定。
在尼柯尔斯图（如图5-68所示）中，可看到尼氏曲线与M（ω）=5.18dB的等M线相切，则可以确定闭环谐振峰值为Mp=5.18dB，且相应的谐振频率为ωp=24.64rad/s。带宽ωb是M（ω）=-3dB时的角频率，从图中可看到曲线与-3dB的等M（ω）dB曲线的交点对应的角频率就是带宽，可以得到ωb=37.7rad/s。
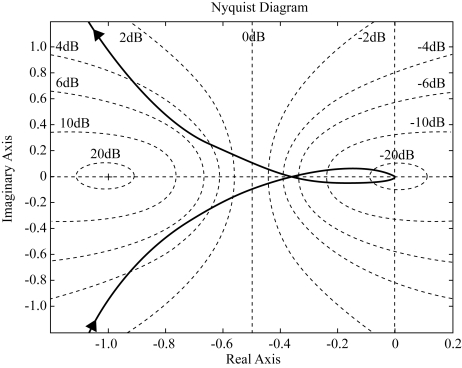
图5-67 系统幅相特性
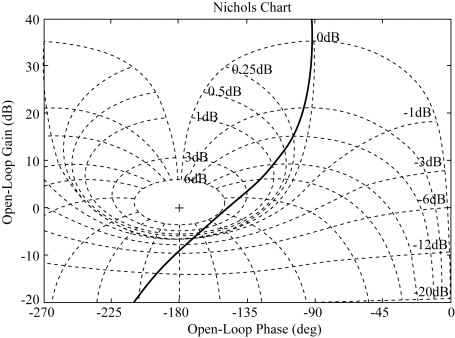
图5-68 系统尼柯尔斯图
可结合伯德图（如图5-69所示）来求取ωp和ωb，在叠印等M线的尼柯尔斯图上找到Mp=5.18dB和M（ω）=-3dB对应的开环对数幅值Lp（ω）=-1.19dB和Lb（ω）=-7.56dB，并且在伯德图上可以找到相应的角频率，ωP=24.64rad/s和ωb=37.7rad/s。
在奈氏图（见图5-67）中也可以叠印等M线，幅相频率特性曲线与M（ω）=5.18dB的等M线相切，则可以确定Mp=5.18dB和ωp=24.64rad/s。带宽ωb是幅相频率特性曲线与M（ω）=-3的等M线相交时的角频率，即ωb=37.7rad/s。
例5-15 系统开环传递函数
确定k=0.5、1、1.5、1.6时，闭环系统的稳态性能和暂态性能。
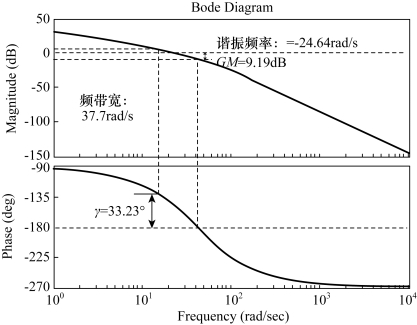
图5-69 系统伯德图
解：MATLAB程序如下。
运行后系统的伯德图、单位阶跃响应曲线及单位斜坡响应曲线分别如图5-70、图5-71和图5-72所示。
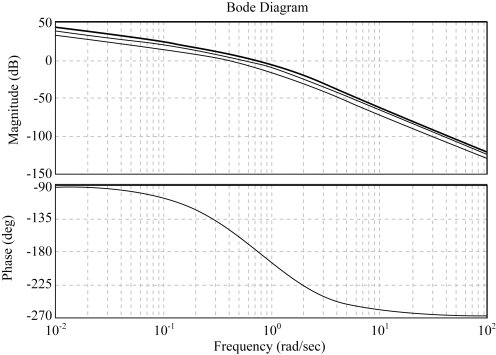
图5-70 系统的伯德图
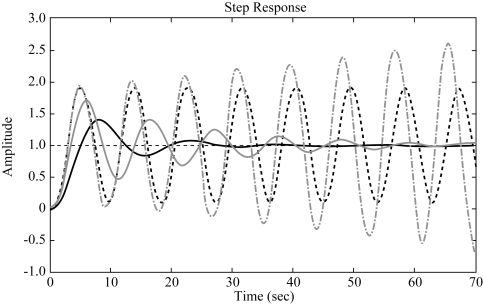
图5-71 系统的单位阶跃响应曲线
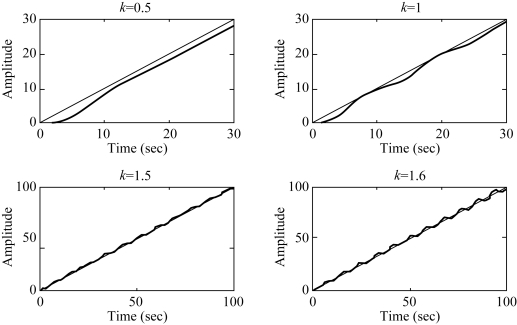
图5-72 系统的单位斜坡响应曲线
在伯德图（见图5-70）中，可看到开环放大系数K的变化，使对数幅频特性垂直上下移动，而不改变系统的相频特性。
（1）稳定性分析
在对数幅频特性中，随着k从0.5增大到1.6，开环幅值穿越频率ωc逐渐增大，ωc1＜ωc2＜ωc3＜ωc4，对应的相位裕量逐渐减小，γ1＞γ2＞γ3=0＞γ4，且γ3=0对应K=1.5。根据稳定裕量判定稳定性，则有K＜1.5时，闭环系统稳定；K=1.5时，闭环系统临界稳定；K＞1.5时，闭环系统不稳定。
闭环系统的稳定性可通过阶跃响应曲线加以验证。在图5-71中，当K=0.5和K=1时，阶跃响应曲线衰减振荡，闭环系统稳定；当K=1.5时，阶跃响应曲线等幅振荡，闭环系统临界稳定；当K=1.6时，阶跃响应曲线发散振荡，闭环系统不稳定。与上述结论一致。
（2）稳态特性分析
例5-15中系统为Ⅰ型系统，则在阶跃输入信号下，稳态误差为零。在斜坡输入下，稳态误差与开环放大系数成反比，见图5-72，当K=0.5时，ess=2；当K=1时，ess=1。稳态误差随着K的增大而减小。而当K=1.5和K=1.6时，斜坡输出响应在稳态值上下分别做等幅振荡和发散振荡。
伯德图的低频段过点（ω=1，L（ω）=20lgK），所以可以通过低频段幅值的大小确定稳态误差的大小。
（3）暂态特性分析
对稳定的系统，即K=0.5和K=1时，在伯德图中ωc1＜ωc2则有闭环系统的响应速度减慢，快速性变差。而γ1＞γ2，则有闭环系统的超调量增大，系统振荡性加强。
在闭环系统的阶跃响应曲线中，可以很容易地得出ts1＜ts2，即随着K的增大，快速性变差。而δ1＜δ2，即随着K的增大，振荡性增强。
由以上分析可知，K的增大虽然可以减小稳态误差，但却使稳定性变差，暂态特性也变差。
有关自动控制原理的文章
- 详细阅读
-
桥梁可靠度分析方法-桥梁可靠度分析方法与应用详细阅读
静定桁架就属于这种结构体系，单元逻辑图如图4.2所示。因尔，从体系可靠度的角度来看，实际的桥梁应尽量避免做成静定结构，条件允许时，应做成具有适当冗余度的超静定结构。超静定结构就是具有这种特性的结构体系。......
2023-09-19
-
车桥耦合振动理论与分析方法《桥梁可靠度分析方详细阅读
由于发动机的振动和路面平整度等原因使得了车-桥系统耦合振动现象更加显著。我国规范中以冲击系数的方式考虑车 -桥耦合振动响应，在实质上该方法是静力分析范畴，不能反映出实际车辆荷载作用下结构的真实响应。图6.11空间车辆模型在车-桥系统的动力响应求解方面主要采用将车辆与桥梁划分为两个子系统，分别建立各自的运动方程，然后建立位移协调和力学平衡条件的方法求解。......
2023-09-19
-
连续刚构桥的可靠度分析方法与应用详细阅读
图3.14主梁截面图为减少计算量，只取主跨的单幅桥进行计算。表3.4系数随机变量分布成桥后的随机变量需要考虑到活载Q2对结构的影响，拟合出的失效模式功能函数为：本章采用响应面法对某高墩大跨连续刚构进行了体系可靠度计算分析。该算例在分析的响应面方法、结构有限元分析和结构可靠度理论的基础上，实现了连续刚构桥的体系可靠度分析。......
2023-09-19
-
部件相对位置公差及其应用详细阅读
图2-12机身测量点Y 向偏离示意图式中：δY——测量点Y 向位置偏差率，‰；δ——前后两测量点高度差的公差，mm；L——两测量点平行于X 轴的水平投影距离，mm。图2-14机身扭转角示意图部件对称性水平测量公差部件对称性测量示意图如图2-15所示，相对偏差率按式计算。图2-15部件对称性水平测量示意图式中：δn——相对偏差率，‰；LZ，LY——左、右侧两个对称尺寸的实测值，mm；L——LZ 和LY 的基本尺寸，mm。......
2023-07-18
-
桥梁可靠度分析方法与应用-验算点法详细阅读
针对中心点法计算精度较低的问题，Hasofer和Lind等提出了验算点法［2］。图2.1当量正态化示意图图2.2n维空间的极限状态曲面图假设受n个非正态分布随机变量影响的结构极限状态方程为：Z＝g（X1，X2，…由公式（2.3）、和联立可求解可靠指标β和验算点。值得注意的是，在由Newton迭代法求出β值后，按式计算原坐标系中的验算点时，应区分正态分布和非态分布参数的μXi值。......
2023-09-19
-
加工误差的统计分析方法与应用详细阅读
由各种工艺因素所产生的加工误差可分为两大类，即系统性误差和随机性误差。机床、夹具、刀具等磨损引起的加工误差，在一次调整后的加工中也均无明显的差异，故也属于常值系统性误差。机床、刀具未达到热平衡时热变形过程中所引起的加工误差，是随加工时间而有规律地变化的，故属于变值系统性误差。......
2023-06-29
-
奈氏稳定性判据解析与应用详细阅读
奈奎斯特稳定判据是Nyquist于1932年最先提出的，它是频率法的系统稳定性判据。奈氏判据是根据系统的开环频率特性，来研究闭环系统稳定性的图解判据，同时能确定系统的相对稳定性。例5-7 某单位负反馈系统的开环传递函数为使用奈氏稳定判据分析系统稳定性。......
2023-06-28
相关推荐