首页理论教育闭环系统频率特性与暂态特性指标的关系分析

闭环系统频率特性与暂态特性指标的关系分析

2025-09-29 理论教育版权反馈

【摘要】：以二阶系统为例，讨论闭环系统频率特性指标及其与暂态特性指标的关系。谐振峰值Mp是闭环系统幅频特性的最大值，如图5-59所示。图5-61闭环系统频率特性指标第3章已得出调节时间ts与系统特征参量之间的关系为将式和式同绘于图5-62，通过阻尼比ζ可以得到Mp与ts的关系。若以二阶系统为例，则谐振角频率ωp与振荡环节在0＜ζ＜0.707产生谐振峰值时的谐振角频率ωr相对应，即图5-62闭环频率特性和时域指标的关系频带宽ωb。

以二阶系统为例，讨论闭环系统频率特性指标及其与暂态特性指标的关系。

典型二阶系统闭环传递函数表达式为

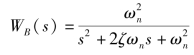
pagenumber_ebook=159,pagenumber_book=148

因此，闭环系统的幅频特性为

pagenumber_ebook=159,pagenumber_book=148

（1）谐振峰值Mp。谐振峰值Mp是闭环系统幅频特性的最大值，如图5-59所示。其值表征了系统单位阶跃响应的相对稳定性。通常，Mp越大，系统单位阶跃响应的超调量δ%也越大。

前面已经给出了Mp与阻尼比ζ之间的关系：

pagenumber_ebook=160,pagenumber_book=149

图5-61给出了Mp与ζ，以及最大超调量δ%与ζ的关系，通过阻尼比ζ可以得到Mp与δ%的关系。

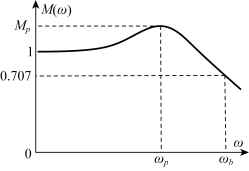
pagenumber_ebook=160,pagenumber_book=149

图5-61　闭环系统频率特性指标

第3章已得出调节时间ts与系统特征参量之间的关系为

pagenumber_ebook=160,pagenumber_book=149

将式（5-74）和式（5-75）同绘于图5-62，通过阻尼比ζ可以得到Mp与ts的关系。(https://www.chuimin.cn)

（2）谐振角频率ωp。谐振角频率ωp是闭环系统幅频特性出现谐振峰值时的频率，见图5-61。若以二阶系统为例，则谐振角频率ωp与振荡环节在0＜ζ＜0.707产生谐振峰值时的谐振角频率ωr相对应，即

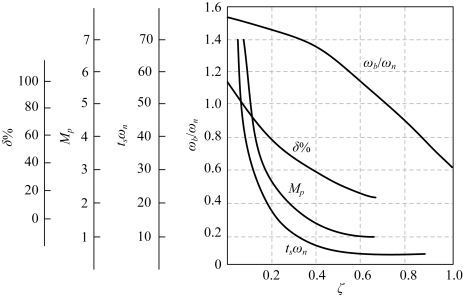
pagenumber_ebook=160,pagenumber_book=149

图5-62　闭环频率特性和时域指标的关系

（3）频带宽ωb。闭环系统频率特性幅值，由其初始值M（0）减小到0.707M（0）时的频率（或由ω=0的增益减低3dB时的频率），称为频带宽ωb，见图5-61。

其物理意义是：低于ωb的正弦输入信号基本可以从系统的输入端传递到输出端，而高于ωb的正弦输入信号将会被不同程度地衰减，即对高频干扰的过滤能力较差。

由式（5-73），令M（ω）=0.707，则可求得频带宽ωb，由

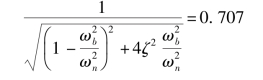
pagenumber_ebook=161,pagenumber_book=150

解之得

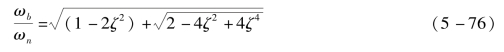
pagenumber_ebook=161,pagenumber_book=150

将与ζ的关系也绘于图5-62中。由图5-62可见，ωb与阻尼比成反比，根据第3章的结论，二阶系统的上升时间、调节时间与阻尼比成反比，则有系统的单位阶跃响的响应速度与带宽ωb成正比，即频带越宽，上升时间越短。对于任意阶次的控制系统，这一关系仍然成立。

根据前面分析，控制系统的幅值穿越频率ωc描述了系统的响应速度，而频带宽也反映了系统的响应速度。一般情况下，系统开环幅值穿越频率ωc的大小就决定了闭环频率特性的频带宽ωb。二阶系统及高阶系统由于会产生闭环谐振峰值，所以ωb一般要大于ωc，但相差不大。

（4）剪切速度。剪切速度是指在高频时频率特性衰减得快慢。在高频区衰减越快，对于有用信号和干扰信号的分辨能力越强。但往往是剪切速度越快，谐振峰值越大。