开环频率特性与时域性能指标关系深析

2025-09-29 理论教育版权反馈

【摘要】：相位裕量为将式带入得这就是相位裕量γ（ωc）这一频率特征量与阻尼比ζ这一特征参数的关系。频率特性的一个重要性质是频率与时间成反比性质。但对于高阶系统，开环频域性能指标和时域指标之间的关系是很复杂的。

因为二阶系统比较简单，而且具有典型意义，所以下面以二阶系统为例分析它们的关系。

1.相位裕量γ（ωc）和超调量δ%之间的关系

典型二阶系统开环频率特性为

pagenumber_ebook=156,pagenumber_book=145

第5.3节中给出了其对数频率特性曲线，现确定幅值穿越频率ωc和ζ之间的关系。由于ω=ωc时，A（ωc）=1，得

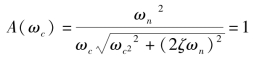
pagenumber_ebook=156,pagenumber_book=145

求解得

有了ωc和ζ之间的关系，就可以求得相位裕量γ（ωc）和ζ的关系。相位裕量为

将式（5-64）带入（5-65）得

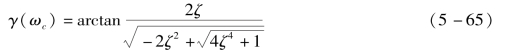
pagenumber_ebook=157,pagenumber_book=146

这就是相位裕量γ（ωc）这一频率特征量与阻尼比ζ这一特征参数的关系。

第3章中，已得到了系统最大超调量δ%和系统阻尼比ζ之间的关系，现将系统阻尼比ζ和最大超调量δ%及相位裕量γ（ωC）的关系绘于图5-57中。通过图5-57，当已知系统的相位裕量时，即可查得对应的超调量。

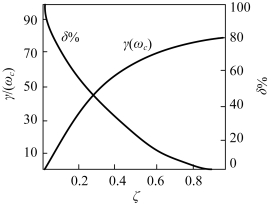
pagenumber_ebook=157,pagenumber_book=146

图5-57　ζ与γ（ωc）和δ%的关系

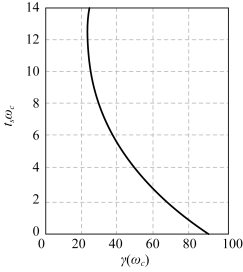
pagenumber_ebook=157,pagenumber_book=146

图5-58　γ（ωc）和tsωc的关系(https://www.chuimin.cn)

2.相位裕量γ（ωC）和调节时间ts之间的关系

相位裕量γ（ωC）和ζ的关系式如（5-65），在第3章已求得调节时间ts的近似表达式为

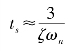
pagenumber_ebook=157,pagenumber_book=146

将式（5-64）代入得

由式（5-65）和式（5-66）可得

这是二阶系统tsωc与γ（ωC）之间的关系，绘成曲线于图5-58。由此可以看出，调节时间ts与相位裕量γ（ωC）有关。如果有两个系统，其γ（ωC）相同，那么它们的超调量也大致相同，但暂态过程时间与ωc成反比，ωc越大，ts越短。

3.幅值穿越频率ωc与调节时间ts的关系

幅值穿越频率ωc在对数频率特性中是一个重要指标，它不仅影响系统的相位裕量，也影响系统的暂态过程时间。

频率特性的一个重要性质是频率与时间成反比性质。在时域分析中，调节时间ts描述了系统响应的快速性，因此幅值穿越频率ωc是闭环系统响应的快速性在频率域中的描述。即ωc越小，ts越大，则系统响应的快速性就越慢；反之，ωc越大，ts越小，则系统响应的快速性就越快。

对于一阶、二阶系统，ωc可以与ts准确对应。但对于高阶系统，开环频域性能指标和时域指标之间的关系是很复杂的。实际上大多数系统的开环频域指标γ和ωc均能反映暂态过程的基本性能。为了说明开环频域指标与时域指标的近似关系，介绍如下两个经验公式：

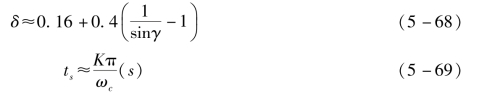
pagenumber_ebook=158,pagenumber_book=147

式中，

由式（5-68）、式（5-69）和式（5-70）可以看出，超调量δ随相位裕量γ的减小而增大；过渡过程时间ts也随γ的减小而增大，但随ωc的增大而减小。

需要指出的是，采用上述公式计算出来的结果往往比实际结果要大。这是因为对高阶系统来说，没有既简单又准确的计算公式，取偏高值可以给设计留有余地。所以，采用上述公式设计出来的系统要进一步调试，通过实践最终确定系统的参数值。

由上面对二阶系统和高阶系统的分析可知，系统开环频率特性中频段的两个重要参数γ、ωc反映了闭环系统的时域响应特性。所以，闭环系统动态性能主要取决于开环对数幅频特性的中频段。