根据式可得系统的开环幅频特性和相频特性。例5-2 某单位负反馈系统为绘制其幅相频率特性的大致曲线。Ⅱ型系统的幅相频率特性如图5-24所示。图5-25例5-3系统的开环幅相频率特性在高频段，A（∞）=0，φ（∞）=-270°。确定开环幅相频率特性与负实轴的方法可根据交点上的特征而定。最小相位系统的开环幅相频率特性满足如下规律。......
2023-06-28
开环放大系数对相位裕量的影响
【摘要】：前面已知幅值穿越频率ωc和开环放大系数K有一定的关系，且和系统型数有关。同样，K值一定，ω1增大时，-40dB/dec的斜率线越远离ωc，对相位裕量的影响越小，所以相位裕量增大。图5-56γmax（ωc）与n之间的关系图可见，合适地选择ωc或K时，将取得最大的相位裕量。中频段的长度对相位裕量有很大影响，中频段越长，相位裕量越大。
前面已知幅值穿越频率ωc和开环放大系数K有一定的关系，且和系统型数有关。下面对三种不同的典型开环对数幅频特性分别讨论。
1.开环频率特性为-1/-2特性
如图5-52所示，其频率特性表达式为
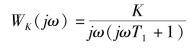
现讨论T1不变时，K对系统的影响。由图5-52知幅值穿越频率ωc发生在低频段，即可得ωc=K。且相位裕量为
γ(ωc)=180°+φ(ωc)=90°-arctanωcT1
显然K增大时，穿越频率ωc增大，-40dB/dec的斜率线更靠近ωc，对相位裕量的影响更大，所以相位裕量减小。同样，K值一定，ω1增大时，-40dB/dec的斜率线越远离ωc，对相位裕量的影响越小，所以相位裕量增大。
2.开环频率特性为-2/-1/-2特性
如图5-53所示，其频率特性表达式为
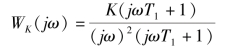
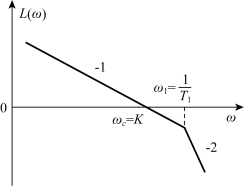
图5-52 放大系数对系统的影响之一
图5-53 放大系数对系统的影响之二
在ω=ωc时，A（ωc）=1，由此求得
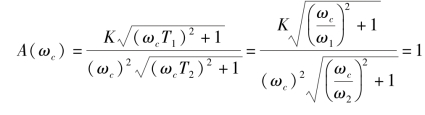
近似得
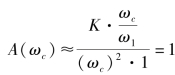
解得
由式（5-61）可看出K对ωc的影响。设T1、T2固定不变，令
，n称为中频宽，通常把穿越频率ωc附近区段称为中频段。因此，相位裕量可写成
可知在一定的n值下，γ（ωc）将随K而变化，但不是单调关系，为此可以用γ（ωc）求导的方法来确定极值。
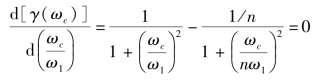
可得
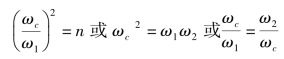
即
总的来说，当K、ω1、ω2满足式（5-62），即ωc恰为ω1、ω2的几何平均值时，γ（ωc）将有最大值。
对式（5-62）两边取对数，得
即ωc在对数频率特性中频段的中点，或中频段对称于ωc，这时相位裕量将有最大值。最大相位裕量为
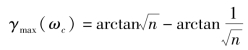
由此可见，最大相位裕量与中频段长度有关，n越大，中频段线段长度越长，最大相位裕量越大。以n作为参变量，γ（ωc）与
的关系曲线如图5-53所示，具有如图5-52所示-2/-1/-2特性。按式（5-62）确定穿越频率的系统，常称为对称最佳系统。而当n=4时，称为三阶工程最佳系统。
3.开环频率特性为-2/-1/-3特性
如图5-54所示，其对数频率特性表达式为
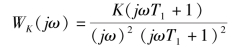
在ω=ωc时，A（ωc）=1，由此求得
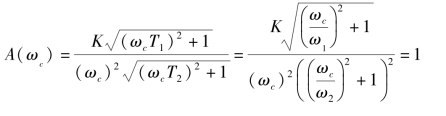
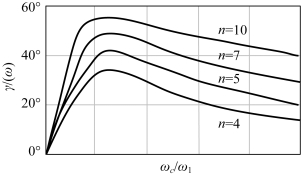
图5-54 γ（ωc）与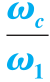
关系曲线
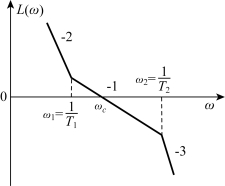
图5-55 放大系数对系统的影响之三
整理得
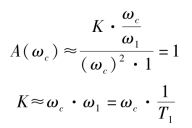
设T1、T2固定不变，令
。因此，相位裕量可写成
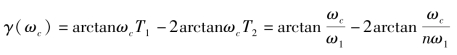
当ωc（或K）为某一值时，γ（ωc）有最大值。可以用γ（ωc）求导的方法来确定极值：
解之得，当
时，γ（ωc）有最大值。当ω2≫ω1时，可以认为ωc≈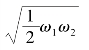
此时，相位裕量γ（ωc）最大。最大相位裕量为
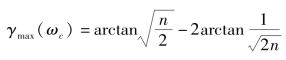
最大相位裕量γmax（ωc）与频比n之间的关系曲线如图5-56所示。
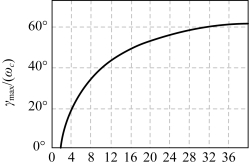
图5-56 γmax（ωc）与n之间的关系图
可见，合适地选择ωc或K时，将取得最大的相位裕量。 -2/-1/-2特性和-2/-1/-3特性系统区别不大，由于后者较前者高频段斜率更大，因此为得到较大的γ（ωc），2/-1/-3特性系统的ωc就要前移，更靠近ω1些，以削弱ω2以后特性的影响。
由此可见，不仅增加放大系数会降低系统的稳定性，降低放大系数也将降低系统的稳定性。有的系统，降低放大系数后甚至会造成不稳定。开环放大系数下降到一定程度时，系统由稳定变为不稳定的系统，常称为条件稳定系统。
所以，一个设计合理的系统，在低频段要满足稳态精度的要求。对于中频段，要注意到暂态特性的要求以确定其线段的形状。中频段形状大致如下。
（1）穿过ωc的幅频特性斜率以-20dB/dec为宜，一般不超过-30dB/dec。
（2）低频段和高频段可以有更大的斜率。低频段有斜率更大的线段可以提高系统的稳态指标；高频段有斜率更大的线段可以更好地排除高频干扰。
（3）中频段的穿越频率ωc的选择，决定于系统暂态响应速度的要求。
（4）中频段的长度对相位裕量有很大影响，中频段越长，相位裕量越大。
有关自动控制原理的文章
- 详细阅读
-
确定系统开环放大系数k的优化方法详细阅读
改变系统的开环放大系数k时，开环伯德图的幅频曲线只升高或降低一个常数，曲线的形状不变，其相频曲线也不变。图12-9 伯德图法确定开环放大系数k4）若考虑的是系统对一般输入指令或干扰信号的误差，则该误差可由各自的误差传递函数的总增益求出。......
2023-06-15
-
干涉量对结构强度的影响优化详细阅读
图4-21试件疲劳寿命与铆接干涉量的关系尽管干涉铆接的抗疲劳性能优于普通铆接，但其抗剪静强度却略低于普通铆接。过分的径向干涉量不仅导致疲劳寿命低于最佳值，而且对于7075-T6 高强铝合金材料，干涉量超过3.2%时，分类试验便已显示其对应力腐蚀开裂的敏感性。导致了干涉配合连接件在无外载时的应力腐蚀敏感性，而干涉量愈大，构件的应力腐蚀敏感性亦愈大。......
2023-07-18
-
调相机对特高压直流系统电压稳定裕度的影响详细阅读
在电力系统中装置同步调相机以维持系统的电压水平，同步调相机同样能改善系统的静态稳定。当电力系统运行方式改变时，通过调节同步调相机的励磁电流，以改变调相机的无功出力，从而将系统中某一节点电压维持在一定水平，以改善系统的电压质量。而调相机可以迅速动作，弥补系统无功缺额，在一定程度上补充瞬时无功功率，提高系统静态电压稳定裕度。......
2023-06-29
-
地下水开采对补给、排泄、储存和开采量的影响分详细阅读
多年平均时，式可近似地表示为地下水开采后，引起天然状态下补排关系的变化，补给量增加，人工排泄量增加，而天然排泄量减少。此时，地下水均衡式为式中:Qme为地下水开采量;Qmf地下水开采状态下的补给量;Qd为地下水开采状态下的排泄量。当地下水补给条件差，增加的天然补给量和减少的天然排泄量不能抵偿开采量时，则需长期消耗储存量。......
2023-06-30
-
交流输电断面增长方式对直流系统电压稳定裕度的详细阅读
改变交直流混合系统中，与直流输电密切相关的交流断面潮流，来分析交流断面潮流变化对换流母线电压稳定性的影响。本小节研究连续型潮流计算过程中，功率增长模式对特高压直流换流母线电压稳定性的影响。......
2023-06-29
-
故障量对风电场送出线路保护的影响详细阅读
由于风电场短路容量比一般较小，因此系统侧工频故障电流远大于风电场侧，使其对电流差动保护的影响降低。送出线路方向保护需要对线路区内、外故障时线路两侧故障方向进行判断。送出线路风电场侧的选相元件需要根据风电场侧电流信息判断。......
2023-06-28
-
同频正弦量相位差的概念和计算详细阅读
为了比较两个同频率的正弦量在变化过程中的相位关系和先后顺序，我们引入相位差的概念，相位差用φ表示。若已知ψ1=30°，ψ2=90°，则电流i1与i2在任意瞬时的相位之差为相位差角φ和初相的规定相同，均不得超过±180°。解：工频电角频率ω=314rad/s电压的解析式为相位差角φ和初相的规定相同，均不得超过±180°。......
2023-06-24
相关推荐