首页理论教育如何保证系统稳定可靠？

如何保证系统稳定可靠？

2023-06-28 理论教育版权反馈

【摘要】：在系统的开环频率特性中，度量相对稳定性的指标是相位裕量和増益裕量。图5-44相位裕量2.增益裕量在相角位移φ（ωj）=-180°时的角频率ωj称为相位穿越频率；在ω=ωj时，幅相频率特性的幅值A（ω）的倒数称为系统的增益裕量，记为GM。但是，仅用增益裕量或者仅用相位裕量，都不足以说明系统的相对稳定性。为了确定系统的相对稳定性，必须同时给出这两个量。

在第3章中已经给出了相对稳定性的概念，并且用根的负实部距离虚轴的远近来代表相对稳定性。在频域法中，闭环系统稳定性取决于Wk（jω）曲线包围（-1，j0）点的圈数，在稳定性研究中，称（-l，j0）点为临界点，Wk（jω）曲线相对于临界点的程度反映系统的相对稳定性。进一步分析和工程应用表明，相对稳定性亦影响系统时域响应的性能。

在系统的开环频率特性中，度量相对稳定性的指标是相位裕量和増益裕量。

1.相位裕量

系统幅值A（ωC）=1或L（ωC）=0时的角频率ωC称为系统的幅值穿越频率，用相角位移φ（ωC）距离-180°的角度值来衡量系统的相对稳定性，称为相位裕量γ（ωC），如图5-44所示，即

相角位移φ（ω）是从正实轴算起，顺时针方向取负。而相位裕量γ（ωC）是从负实轴算起，逆时针方向规定为正，顺时针方向为负。

相位裕量γ（ωC）的含义是，对于闭环稳定系统，如果系统开环相频特性再滞后γ（ωC）度，则系统将处于临界稳定状态。为了使最小相位系统稳定，γ（ωC）必须是正值。

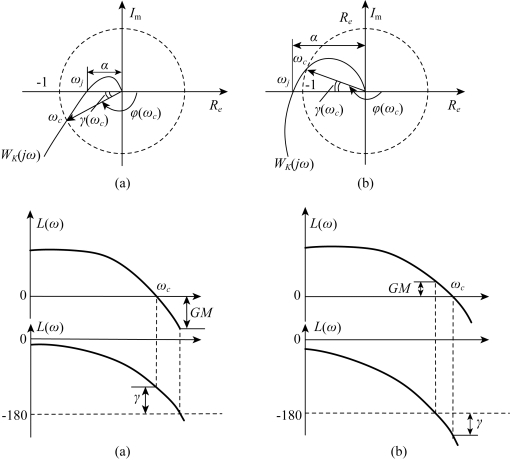
pagenumber_ebook=147,pagenumber_book=136

图5-44　相位裕量

2.增益裕量

在相角位移φ（ωj）=-180°时的角频率ωj称为相位穿越频率；在ω=ωj时，幅相频率特性的幅值A（ω）的倒数称为系统的增益裕量，记为GM。

pagenumber_ebook=148,pagenumber_book=137

增益裕量GM的含义是，对于闭环稳定的系统，如果系统开环幅频特性再增大GM倍，则系统将处于临界稳定状态。

对数坐标下，增益裕量按下式定义：

当α＜1时，增益裕量的分贝数为正值，对于最小相位系统，闭环系统稳定；当α＞1时，增益裕量的分贝数为负值，对于最小相位系统，闭环系统不稳定；当α=1时，增益裕量的分贝数为零，对于最小相位系统，闭环系统临界稳定。

控制系统的相位裕量γ（ωC）和增益裕量GM是极坐标图对（-l，j0）点靠近程度的一种度量。因此，这两个量可以用来作为设计准则。但是，仅用增益裕量或者仅用相位裕量，都不足以说明系统的相对稳定性。为了确定系统的相对稳定性，必须同时给出这两个量。

为了得到较好的动态性能，要求相位裕量应当在γ（ωC）=30°～60°之间，而增益裕量GM＞=6dB。对于最小相位系统而言，为保证系统有足够的相位裕量，对数幅频特性应以-20dB/dec的斜率穿越0dB线。如果以-40dB/dec的斜率穿越0dB线，则可能是不稳定的，即使稳定，其相位裕量也比较小。