奈奎斯特稳定判据是Nyquist于1932年最先提出的，它是频率法的系统稳定性判据。奈氏判据是根据系统的开环频率特性，来研究闭环系统稳定性的图解判据，同时能确定系统的相对稳定性。例5-7 某单位负反馈系统的开环传递函数为使用奈氏稳定判据分析系统稳定性。......
2023-06-28
应用奈氏判据的例子
【摘要】：例5-9 系统开环传递函数为应用奈氏稳定判据分析闭环系统稳定性。完整的开环幅相频率特性如图5-40所示。例5-12 设系统的开环传递函数为图5-42开环幅相频率特性试用对数频率稳定判据判断闭环系统的稳定性。图5-43系统伯德图由图5-43可见，在L（ω）＞0区段，相频特性曲线φ（ω）负穿越-180°线一次，根据奈氏稳定判据，N+≠N-，即闭环系统不稳定。
下面举例说明怎样应用奈氏判据，根据开环幅相频率特性来判断闭环系统的稳定性。开环幅相频率特性可以根据几个关键点绘出，或者在MATLAB中使用命令绘出。
例5-8 系统开环传递函数为
应用奈氏稳定判据分析闭环系统的稳定性。
解：由开环传递函数知，开环全部极点位于s左半平面，系统为最小相位系统，即P=0。
又开环系统为0型系统，开环幅相频率特性的起点在正实轴上一点（K，j0），以-180°终止于原点，其大致曲线如图5-39所示。虚线部分表示为ω从-∞→0时的幅频率相特性曲线，与正频率部分关于实轴对称。
图5-39 系统开环幅相位频率特性曲线
根据奈氏稳定判据，由于曲线不包围（-1，j0）点，所以无论开环增益K怎样变化，闭环系统总是稳定的。这是二阶系统的特点，与根轨迹法及劳斯判据得到的结论一致。
例5-9 系统开环传递函数为
应用奈氏稳定判据分析闭环系统稳定性。
解：由开环传递函数知，系统为最小相位系统，即P=0。开环频率特性可以表示为
其幅相频率特性的大致曲线在例5-3中已绘出。
开环系统为Ⅰ型系统，在原点处有一开环极点，则Ⅰ型系统的幅相频率特性的低频段需要添加增补线，在ω从0变化到0+时，Wk（jω）以∞为半径，从正实轴无穷远起始，顺时针旋转90°，即A（0）=∞，φ（0）=0°。
完整的开环幅相频率特性如图5-40所示。
图5-40 开环幅相频率特性
由图可以看出，当
时，即
，当ω从-∞→+∞，Wk（jω）曲线顺时针包围（-l，j0）点两圈，即N=-2，故得Z=P-N=2，这时闭环系统在s右半平面有2个极点，闭环系统不稳定。
当
时，Wk（jω）曲线与（-1，j0）点相交，闭环系统临界稳定。
当
时，Wk（jω）曲线不包围（-1，j0）点，N=0，闭环系统稳定。
例5-10 系统开环传递函数为
应用奈氏稳定判据分析闭环系统稳定性。
解：由开环传递函数知，系统为最小相位系统，即P=0。
开环频率特性为
其中，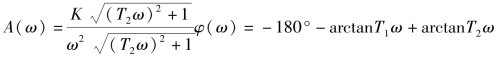
下面分几种情况讨论开环幅相频率特性及其稳定性。
（1）T1＞T2的情况。在低频段ω→0+，A（0）=∞，由于arctanT1ω＞arctanT2ω，所以当ω从0+增加时，φ（ω）＜-180°，位于第二象限，ω从0→0+的增补线如图5-41（a）所示；在高频段ω→∞，A（∞）=0，φ（ω）=-180°，即幅相特性以-180°趋于坐标原点。大致的幅相特性曲线如图5-41（a）所示。
由图看出，ω从-∞→+∞时，Wk（jω）曲线顺时针包围（-l，j0）点两圈，N=-2，故得Z=N-P=2。这时闭环系统在s右半平面有2个极点，闭环系统不稳定。
（2）T1＜T2的情况。在低频段ω→0+，A（0）=∞，由于arctanT1ω＜arctanT2ω，所以当ω从0+增加时，φ（ω）＞-180，位于第三象限，ω从0→0+的增补线如图5-41（b）所示；在高频段ω→∞，A（∞）=0，φ（ω）=-180°，即幅相特性以-180°趋于坐标原点。大致的幅相特性曲线如图5-41（b）所示。
由图看出，ω从-∞→+∞时，Wk（jω）曲线不包围（-1，j0）点，N=0，闭环系统稳定。
（3）T1=T2的情况。此时，在ω从-∞→+∞时，φ（ω）=-180°时，即幅相特性曲线沿负实轴变化，如图5-41（c）所示。
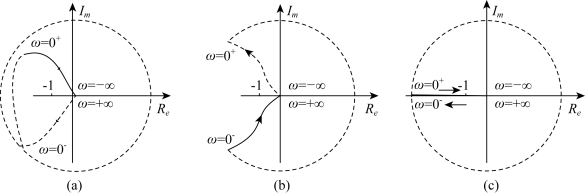
图5-41 系统幅相特性曲线
由图看出，Wk（jω）曲线正好通过（-l，j0）点，闭环系统临界稳定。
例5-11 系统开环传递函数为
应用奈氏稳定判据分析闭环系统稳定性。
解：由开环传递函数知，在s右半平面有一个开环极点，系统为非最小相位系统，P=1，系统开环频率特性为
其中，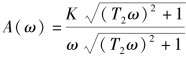
，φ（ω）=-270°+arctanT1ω+arctanT2ω
或表示为代数形式
Wk(jω)=P(ω)+jQ(ω)
其中，
在低频段，A（0+）=∞，φ（0+）=-270°。低频段的特性由平行于虚轴的渐近线决定，渐近线与实轴交点为
开环系统为Ⅰ型系统。在原点处有一开环极点，则Ⅰ型系统的幅相频率特性的低频段需要添加增补线，在ω=0时，A（0）=∞，φ（0）=-180°；ω从0变化到0+时，幅相频率特性以∞为半径，顺时针旋转90°到ω=0+的位置，如图5-42所示。
在高频段，A（∞）=0，φ（∞）=-90°。
求开环幅相频率特性与负实轴的交点，可令
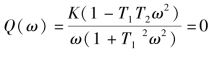
解得
，再代入P（ω）得
完整的开环幅相频率特性如图5-42所示。
闭环系统稳定性与幅相特性形状有关。当-KT2＜-1时，即
时，曲线逆时针包围（-1，j0）点一圈，即N=1，则Z=P-N=0，闭环系统稳定；当-KT2=-1时，曲线与（-1，j0）点相交，闭环系统临界稳定；当-KT2＞-1时，曲线顺时针包围（-1，j0）点一圈，即N=-1，则Z=P-N=2，闭环系统不稳定。
例5-12 设系统的开环传递函数为
图5-42 开环幅相频率特性
试用对数频率稳定判据判断闭环系统的稳定性。
解：对数频率特性如图5-43所示，伯德图的绘制可由渐近线特性表示，也可通过MATLAB绘制。本例由MATLAB绘制。
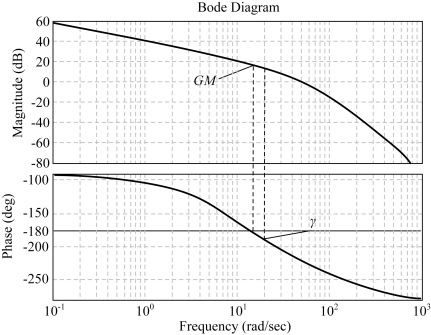
图5-43 系统伯德图
由图5-43可见，在L（ω）＞0区段，相频特性曲线φ（ω）负穿越-180°线一次，根据奈氏稳定判据，N+≠N-，即闭环系统不稳定。
有关自动控制原理的文章
- 详细阅读
-
劳斯判据的应用方法的分析介绍详细阅读
除此之外，劳斯判据还有以下方面的应用。图3-20系统结构图解：系统的闭环传递函数为系统的特征方程为6s3+5s2+s+K=0。列出劳斯表为由劳斯判据可知，系统稳定的充要条件为，即K取值范围为。图3-22系统增加比例微分控制其闭环系统的传递函数变为特征方程为 2s3+s2+Kτs+K=0列出劳斯表为根据劳斯判据，系统稳定的条件为，可见只要选取适当的参数，系统便可稳定。......
2023-06-28
-
拉氏变换性质|复变函数及应用详细阅读
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a ＞0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30
-
拉氏变换定理存在-复变函数及其应用详细阅读
可以看出,拉式变换存在的条件要比傅氏变换存在的条件弱得多,但是对一个函数作拉氏变换也要具备一定的条件.对f提什么要求才能使f与指数衰减函数e-αt 的乘积在无穷区间上绝对可积？实数α=Re=Re应该取多大呢？......
2023-10-30
-
顿号的使用规则及例子详细阅读
顿号只能放在句内，且只能用在并列词语或词组之间。瞿塘峡、巫峡、西陵峡，每一个峡谷都浓缩得密密层层，再缓慢的行速也无法将它们化解开。例2中的并列词语“瞿塘峡、巫峡、西陵峡”作主语，用顿号分隔以表示并列关系。上面例1中的“一年、两年、三年”是在表示递升的数量词语之间应用顿号。上面例子中的“一、二、三”是次序语，后面应当用顿号表示停顿。......
2023-07-30
-
柯氏培训评估模型应用问题详细阅读
因此,柯氏培训评估模型评估方法的改进会是今后柯氏培训评估模型发展的一个方向。这也是现在国内大多数组织不愿意将柯氏评估模型彻底应用的一个重要原因。......
2023-12-03
-
文氏流量计的测速原理及应用详细阅读
3.3.1 测速原理文氏流量计是一种用来测量封闭管道中单相稳定流体流速的测速装置，常用于测量空气、天然气、煤气、水等流体的体积流率或流速，通常所测的流体流动是液体与低速气体流动。......
2023-06-29
-
数据库技术与应用教程中的一个简单例子详细阅读
首先通过一个简单的例子来看一下查询优化的必要性。设每块能装10个元组，则写出这些块要用5×104s。满足条件的元组假设仅50个，均可放在内存中。因此，第1种情况下执行查询的总时间≈105＋2×5×104≈105。自然连接的结果比广义笛卡儿积减少了很多，为104个，所以写出这些元组的时间为50s，仅为第1种情况的千分之一。总的存取时间将进一步减少到数秒。......
2023-11-24
相关推荐