如何判断对数频率的稳定性

2023-06-28 理论教育版权反馈

【摘要】：为了更好地判断其包围点的圈数，在WK平面上定义如下概念。根据正负穿越可将奈氏稳定判据表述如下：对于最小相位系统，P=0，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为0时，闭环系统是稳定的，否则闭环系统不稳定；对于非最小相位系统，设系统开环传递函数有P个极点在右半s平面，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为P/2时，闭环系统是稳定的，否则闭环系统不稳定。

因ω自-∞→-0→+0→+∞→-∞时，WK（jω）奈氏曲线对称于实轴，因此，实际应用中常常只画ω=0→∞的那一部分，即半闭合曲线WK（jω）。为了更好地判断其包围（-1，j0）点的圈数，在WK平面上定义如下概念。

正穿越一次：WK（jω）曲线由上向下穿越（-1，j0）点左侧的负实轴一次，用N+表示。

负穿越一次：WK（jω）曲线由下向上穿越（-1，j0）点左侧的负实轴一次，用N-表示。

正穿越半次：WK（jω）曲线由上向下终止于或起始于（-1，j0）点左侧的负实轴。

负穿越半次：WK（jω）曲线由下向上终止于或起始于（-1，j0）点左侧的负实轴。

注意到，如果ω=0→∞变化时，WK（jω）曲线按逆时针方向绕（-1，j0）点一圈，则必正穿越一次；反之，若顺时针方向绕（-1，j0）点一圈，则必负穿越一次。

根据正负穿越可将奈氏稳定判据表述如下：对于最小相位系统，P=0，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为0时，闭环系统是稳定的，否则闭环系统不稳定；对于非最小相位系统，设系统开环传递函数有P个极点在右半s平面，当ω=0→∞，在复平面上WK（jω）正穿越和负穿越次数之差为P/2时，闭环系统是稳定的，否则闭环系统不稳定。

开环系统幅相频率特性与对数频率特性之间存在如下对应关系（如图5-38所示）：WK（jω）平面上，的单位圆，对应于对数幅频特性的0分贝线；WK（jω）平面上单位圆外的区域，对应于对数幅频特性0分贝线以上的区域；WK（jω）平面上的负实轴，对应于对数相频特性上的φ（ω）=-180°线。由此，正负穿越的概念可在半对数坐标平面上定义：当幅相频率特性正穿越时，相角位移有正的增量，等价于在L（ω）＞0dB时，φ（ω）由下向上穿越-180°线；当幅相频率特性负穿越时，相角位移有负的增量，等价于在L（ω）＞0dB时，φ（ω）由上向下穿越-180°线，如图5-38（b）所示。

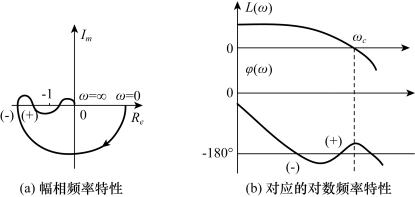
pagenumber_ebook=142,pagenumber_book=131

图5-38　频率特性的正负穿越

根据上述对应关系，利用对数频率特性判断闭环系统稳定性的奈氏稳定判据表述如下：对于最小相位系统，P=0，则在L（ω）＞0dB的所有频段内，对数相频特性与-180°线正穿越和负穿越次数之差为0时，闭环系统是稳定的，否则闭环系统不稳定；对于非最小相位系统，设系统开环传递函数有P个极点在右半s平面，则在L（ω）＞0dB的所有频段内，对数相频特性与-180°线正穿越和负穿越次数之差为P/2时，闭环系统是稳定的，否则闭环系统不稳定。

如何判断对数频率的稳定性

相关推荐