单列角接触球轴承 单列角接触球轴承有以下几种结构形式：1）分离型角接触球轴承。图1-18 角接触球轴承a）单列角接触球轴承 b）双列角接触球轴承 c）角接触球轴承结构2）非分离型角接触球轴承。双列角接触球轴承 双列角接触球轴承的特点是可以同时承受径向和轴向载荷的联合载荷，限制轴的两方向的轴向位移。图1-21 两面带防尘盖和两面带密封圈的双列角接触球轴承图1-22 有装球缺口的双列角接触球轴承的安装......
2025-09-29
辐角定理：复数变量s平面内的极点和零点辐角之和相等
【摘要】：s是复数变量，在s平面上可表示为s=σ+jω。不失一般性，取s平面上F的零点、极点及闭合路径，如图5-34所示。图5-34辐角定理示意图当s沿ΓS绕行时，∠和∠将随之变化。由式得式中，为F所有零点辐角之和；为F所有极点幅角之和。假设F在Γs之内有Z个零点和P个极点，当s沿Γs顺时针方向绕行一圈时，F的相角变化为相角变化-2π相当于ΓF按顺时针方向包围F平面的坐标原点一圈。
s是复数变量，在s平面上可表示为s=σ+jω。F（s）是s的有理分式函数，在平面F（s）上表示为F（s）=μ+jν。在s平面上除了F（s）的零点和极点外的任意点si，均可在F（s）平面上找到与之对应的点F（si）。所以，复函数F（s）就是从s平面到F（s）平面的映射，这种映射是一一对应的。在s平面上任选一条闭合路径Γs，它不通过F（s）的任一零点和极点，s沿Γs顺时针运动一周，则相应地在F（s）平面上亦形成一条闭合路径ΓF。
不失一般性，取s平面上F（s）的零点、极点及闭合路径，如图5-34（a）所示。
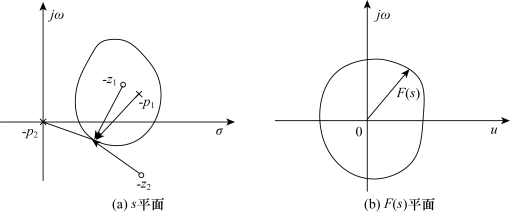
图5-34 辐角定理示意图
当s沿ΓS绕行时，∠（s+zi）和∠（s+pj）将随之变化。若F（s）的零点（如-z2）、极点（如-p2）在Γs之外，则s沿Γs绕一圈，其相角变化皆等于零；若F（s）的零点或极点（如-z1或-p1）在Γs之内，则s沿Γs顺时针方向绕一圈，矢量（s+zi）或（s+pj）相角变化为-2π。
由式（5-51）得
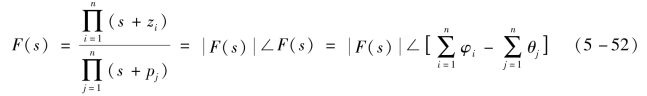(https://www.chuimin.cn)
式中，
为F（s）所有零点辐角之和；
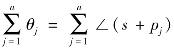为F（s）所有极点幅角之和。
假设F（s）在Γs之内有Z个零点和P个极点，当s沿Γs顺时针方向绕行一圈时，F（s）的相角变化为
相角变化-2π相当于ΓF按顺时针方向包围F（s）平面的坐标原点一圈。故表示ΓF包围F（s）平面坐标原点的圈数为N=P-Z；ΓF顺时包围原点，N为负；ΓF逆时针包围原点，N为正。
辐角定理：假定在s平面上取闭合路径Γs，包围F（s）的零点数为Z、极点数为P，s顺时针方向沿Γs绕一圈，则在F（s）平面上与之对应的闭合路径ΓF绕原点的圈数为
N=P-Z
若N＞0，则ΓF逆时针包围原点；若N=0，则ΓF不包围原点；若N＜0，则ΓF顺时针包围原点。
相关文章
- 详细阅读
-
生成角点标记图的方法详细阅读
标记图是一种一维函数的边界表达方法，其典型的生成方法是将从质心到边界线的距离转化成一个角度函数，如图7-8所示。本书提出的角点标记图将标记图的基本思想应用于构造角点特征的过程中，并在保存目标基本信息的同时消除其对尺寸和旋转的依赖性，使得该特征具有平移不变形、比例不变性和旋转不变性。这种模式向量的生成方法依赖于旋转和比例缩放变换。......
2025-09-29
-
平面内点与直线的关系详细阅读
图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2025-09-29
-
最小轴向载荷对14推力和推力角接触轴承的影响详细阅读
接触角不等于零的角接触球轴承和滚子轴承，在运转中滚动体的自转轴线方向是经常变化的。如为钢制球：J0=4.2×10-8D5w图2-84表示推力向心滚子轴承作用于滚动体上的惯性力矩的方向。图2-86表示角接触球轴承中惯性力矩的方向。推力轴承和推力向心轴承中惯性力矩最大。表2-60 系数k值在多数情况下，推力轴承的实际载荷超过最小轴向载荷的计算值，此时轴承不需要预紧。对于推力球轴承，在某些情况下，无法克服由于惯性力矩引起的滑动。......
2025-09-29
-
推力球轴承和双向推力角接触球轴承的优化设计详细阅读
推力球轴承只能承受轴向载荷，单向推力球轴承只能承受一个方向的轴向载荷，双向推力球轴承可以承受两个方向的轴向载荷。单向推力球轴承可以限制轴和壳体的一个方向的轴向位移，双向轴承可以限制两个方向的轴向位移。如果安装条件许可，可以使用带球面座圈的单向或双向推力球轴承。......
2025-09-29
-
计算换相重叠角的方法及应用详细阅读
根据以上分析及结果，再经进一步分析可得出以下变压器漏感对整流电路影响的一些结论：①出现换相重叠角γ，整流输出电压平均值Ud 降低。⑤换相使电网电压出现缺口，成为干扰源。解因为换相压降的等效内阻又因为当α=0°时，cos γ=1-0.035=0.965，所以换相重叠角......
2025-09-29
-
不同PVT角下的综合优化设置方法详细阅读
比如，芯片某条时序路径的hold违例可能不是发生在PVT最快的情况下，而在数据路径为最快、时钟路径为较快的路径上，因此我们需要针对时序检查的数据路径和时钟路径采用不同的PVT参数来保证芯片流片后能够正常工作。需要使用ICC中的scenario来将芯片的不同工作状态，用不同PVT参数的搭配区分开来。......
2025-09-29
-
角点特征的技巧的分析介绍详细阅读
由于SUSAN算法不依赖于目标分割得到的轮廓信息，所以无法通过跟踪轮廓来得到角点的顺序，并依此计算每个角点的权重，进行特征空间的优化。两种角点检测算法及其相应的特征空间优化方法的效果，如图7-7所示。图7-7 对角点特征空间进行优化设计～e）是进行特征选择，g）～i）是进行特征的组合优化）......
2025-09-29
相关推荐