开环传递函数可分解为基本环节的串联形式，如式和式，在此基础上，系统的开环对数幅频特性和对数相频特性分别为表明开环系统对数频率特性表现为诸基本环节对数频率特性叠加这一简单的形式。在ωωmin频段，系统开环对数幅频特性渐近线表现为分段折线。系统开环对数幅频渐近特性曲线如图5-29所示。图5-29系统对数频率特性注意到此系统中有一个一阶微分环节，将使相角有正的位移偏向。......
2023-06-28
系统开环频率特性的幅度相位特点
【摘要】：根据式可得系统的开环幅频特性和相频特性。例5-2 某单位负反馈系统为绘制其幅相频率特性的大致曲线。Ⅱ型系统的幅相频率特性如图5-24所示。图5-25例5-3系统的开环幅相频率特性在高频段，A（∞）=0，φ（∞）=-270°。确定开环幅相频率特性与负实轴的方法可根据交点上的特征而定。最小相位系统的开环幅相频率特性满足如下规律。
应用频率法分析或研究控制系统，是根据系统的开环频率特性来判断系统的稳定性、计算闭环频率特性、估计系统的时域指标。所以，掌握系统的开环幅相频率特性的绘制方法和规律是很重要的。
要准确绘制系统的开环幅相频率特性曲线比较麻烦，不过在工程实践中，并不需要准确画出整条幅相频率特性曲线，只要知道曲线的走向和主要特征，对曲线的关键部分进行准确计算即可。
系统的开环频率特性为
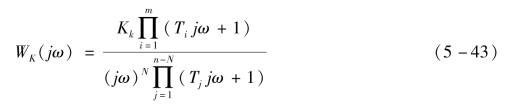
式中，N为开环传递函数中串联的积分环节的个数，也可称为系统的类型。
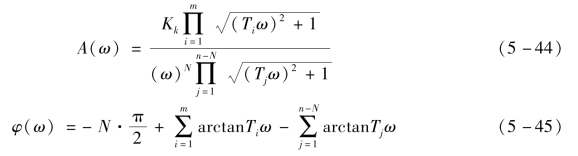
给出不同的ω，计算相应的A（ω）和φ（ω），在直角坐标中得出相应的点。当ω由0变到+∞时，就得到系统开环幅相频率特性。
1.0型系统的开环幅相频率特性
在式（5-44）和式（5-45）中，令N=0得
在ω=0处，A（0）=Kk，φ（0）=0，故0型系统的幅相频率特性起始于实轴上的点（Kk，j0）。
在ω=∞处，由于n＞m，A（∞）=0，φ（∞）=-（n-m）
，故0型系统的幅相频率特性以
的角度终止于原点。
在0＜ω＜∞的区段，频率特性的形状与环节及其参数有关。
例5-1 某单位反馈系统为
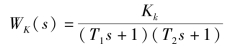
绘制其福相频率特性的大致曲线。
解：系统开环频率特性
为0型系统，根据上面的讨论，
幅相频率特性的起点：A（0）=Kk，φ（0）=0，起始于正实轴上的一点（Kk，j0）。
幅相频率特性终点：
，以-π的角度终止于原点。
幅相频率特性曲线如图5-21所示。
图5-21 例5-1系统的幅相频率特性曲线
如果环传递函数分子上没有时间常数项，则随着频率ω的增大，相角位移φ（ω）将连续减小，从图形看，开环幅相频率特性将顺时针旋转。如果开环传递函数分子上有时间常数项，则随着频率ω的增大，相角位移φ（ω）将不再连续减小，在某些频率上相角位移φ（ω）会有正的增量，从图形看，开环幅相频率特性将出现回转。
例5-2 某单位负反馈系统为
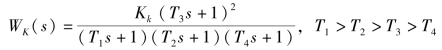
绘制其幅相频率特性的大致曲线。
解：系统的开环频率特性
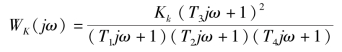
幅相频率特性的低频段：A（0）=Kk，φ（0）=0起始于正实轴上的一点（Kk，j0）。
幅相频率特性的高频段：
，以
的角度终止于原点。
因为分子中存在时间常数项（jωT3+1）2，所以在某一频率范围内将使相角位移系统产生正的增量，这样φ（ω）不再连续减小，奈氏曲线向右弯曲，如图5-22所示。
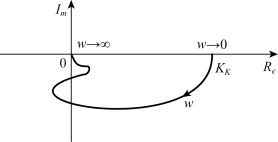
图5-22 例5-2系统的幅相频率特性
2.Ⅰ型系统的开环幅相频率特性
在式（5-44）、式（5-45）中，令N=1，则
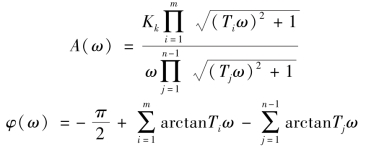
在ω→0+时，A（0+）→∞，φ（0+）→-90°，故Ⅰ型系统的幅相频率特性在ω→0+时，是在-90°方向的无穷远处开始的。
此时，A（ω）趋于无穷大的物理意义可以这样理解：在ω→0+时，相当于在系统输入端加一个恒值信号，由于系统有积分环节，所以开环系统输出量将无限增长。
在ω→∞时，对于n＞m的系统，A（∞）=0；φ（∞）=-（n-m）×90°，故Ⅰ型系统的幅相频率特性以-（n-m）×90°的角度终止于原点。
设（n-m）=4，Ⅰ型系统的幅相频率特性如图5-23所示。
3.Ⅱ型系统的开环幅相频率特性
Ⅱ型系统的传递函数较Ⅰ型系统多串入一积分环节，因此Ⅱ型系统的幅相特性在ω→0+处，A（0+）→∞，φ（0+）→-180°；在ω=∞处，A（∞）=0，φ（∞）=-（n-m）×90°。
Ⅱ型系统的幅相频率特性如图5-24所示。
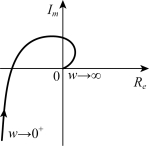
图5-23 Ⅰ型系统的幅相频率特性
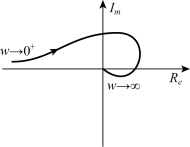
图5-24 Ⅱ型系统的幅相频率特性
例5-3 系统开环传递函数为
绘制其幅相频率特性的大致曲线。
解：开环频率特性可以表示为
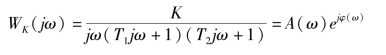
其中，
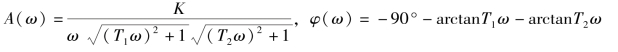
或表示为代数形式
WK(jω)=P(ω)+jQ(ω)
其中，
在低频段，A（0+）=∞，φ（0+）=-90°，低频段的特性由平行于虚轴的渐近线决定。渐近线与实轴交点为
如图5-25中虚线所示。
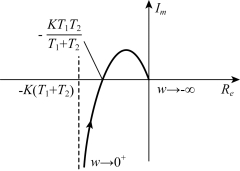
图5-25 例5-3系统的开环幅相频率特性
在高频段，A（∞）=0，φ（∞）=-270°。幅相曲线以-270°终止于原点。
当开环幅相频率特性与负实轴交点时，要确定出其位置，因为这一点很重要，关系到系统稳定性问题。
确定开环幅相频率特性与负实轴的方法可根据交点上的特征而定。例如，令虚频特性Q（ω）=0，求得交点上的频率，再代入实频特性P（ω），即可确定出交点的位置。对于本例，令Q（ω）=0，解得
代入P（ω）得
例5-4 系统开环传递函数为
式中，K、τ、T均大于0，试绘制其幅相频率特性的大致曲线。
解：开环频率特性表示为
其中，
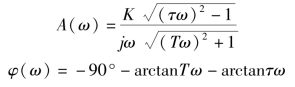
或表示为代数形式
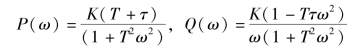
在低频段，A（0+）=∞，φ（0+）=+90°低频段的特性由平行于虚轴的渐近线决定，渐近线与实轴交点为
在高频段，A（∞）=0，φ（∞）=-90°。幅相频率特性曲线以-90°方向终止于原点。开环幅相频率特性与实轴的交点计算如下。令Q（ω）=0，得
则
开环幅相频率特性如图5-26所示。
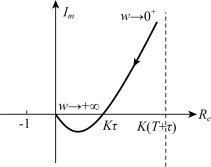
图5-26 例5-4系统的开环幅相频率特性
4.开环幅相频率特性曲线的关键部分
在控制系统中，凡在s右半平面不包含开环极点或零点，且不包含时滞环节的系统，称为最小相位系统，反之称为非最小相位系统。
最小相位系统的开环幅相频率特性满足如下规律。
（1）幅相特性的低频段。
由式（5-43）和式（5-44），当ω→0时，可以确定特性的低频部分，其低频起始位置由系统类型及开环放大系数确定，相位满足N×（-90°），如图5-27所示。
对于0型系统，当ω→0时，特性起始于正实轴上一点（Kk，j0）。对于Ⅰ型系统，特性起始于一条与虚轴平行的渐近线，渐近线与实轴的交点可以由下式确定：
（2）幅相特性的高频段。
当ω→0时，对于n＞m的系统，A（∞）=0，φ（∞）=-（n-m）×90°，即特性以-（n-m）×90°向趋于原点，如图5-28所示。
图5-27 幅相特性的低频段
图5-28 幅相特性的高频段
（3）幅相特性与实轴和虚轴的交点。
特性与负实轴的交点计算方法如下。
①令Im[WK（jω）]=Q（ω）=0，求得交点上的频率，再代入实频特性P（ω）即可确定出交点的位置。
②令φ（ω）=-180°，求得交点上的频率，再代入幅频特性A（ω）即可确定出交点的位置。
求特性与虚轴的交点可令Re[WK（jω）]=P（ω）=0，求得交点上的频率，再代入虚频特性Q（ω）即可确定出交点的位置。
（4）如果在传递函数的分子中没有时间常数项，则当ω由0→∞的过程中，特性的相位角连续减小，特性平滑变化。如果在分子中有时间常数项，则特性的相位角不再连续减小，奈氏曲线会出现凹部。
（5）对于非最小相位系统，其幅频特性的表示与对应的最小相位系统一致，而相频特性的表示则需注意象限的确定。
有关自动控制原理的文章
- 详细阅读
-
开环放大系数对相位裕量的影响详细阅读
前面已知幅值穿越频率ωc和开环放大系数K有一定的关系，且和系统型数有关。同样，K值一定，ω1增大时，-40dB/dec的斜率线越远离ωc，对相位裕量的影响越小，所以相位裕量增大。图5-56γmax（ωc）与n之间的关系图可见，合适地选择ωc或K时，将取得最大的相位裕量。中频段的长度对相位裕量有很大影响，中频段越长，相位裕量越大。......
2023-06-28
-
最小相位和非最小相位系统简介详细阅读
例如，有两个系统，其传递函数分别为根据定义不难判断，W2是最小相位系统，W1是非最小相位系统。图5-30最小相位环节与非最小相位环节对数频率特性的对比根据这一意义，时滞环节是非最小相位环节。最小相位系统有以下特征。在n≥m且幅频特性相同的情况下，最小相位系统的相角变化范围最小。在系统设计时，除了被控对象中可能包含之外，一般不人为引入非最小相位环节。......
2023-06-28
-
正弦交流信号的特点：频率、振幅和相位详细阅读
图6-1 正弦交流信号的波形在正弦交流信号中，随时间按正弦规律做周期变化的量称为正弦量。提示说明振幅值：正弦交流电瞬时值中最大的数值叫做最大值或振幅值。振幅值决定正弦量的大小，通常用Um、Im表示。由于RC正弦波振荡电路主要用于低频振荡，因此要想产生更高频率的正弦信号，应采用LC正弦波振荡电路，振荡频率为，而石英振荡器的特点是其振荡频率特别稳定，因此常用于振荡频率高度稳定的场合。......
2023-06-26
-
开环频率特性与时域性能指标关系深析详细阅读
相位裕量为将式带入得这就是相位裕量γ（ωc）这一频率特征量与阻尼比ζ这一特征参数的关系。频率特性的一个重要性质是频率与时间成反比性质。但对于高阶系统，开环频域性能指标和时域指标之间的关系是很复杂的。......
2023-06-28
-
优化PWM伺服系统的开环机械特性详细阅读
系统采用脉宽调制时，即使在稳态情况下，直流PWM调速系统的转矩和转速也都是脉动的。脉宽调速系统在准稳态下的机械特性是指其平均转速与平均转矩（电流）的关系。前面已介绍的带制动电流通路的不可逆PWM电路、双极式可逆PWM电路、单极式可逆PWM电路，这几种PWM变换器的准稳态的电压、电流波形都是相似的。图4-6带制动的不可逆电路开环机械特性......
2023-06-25
-
开环与闭环系统：反馈和稳定性的区别详细阅读
与之对应，闭环的英文名词：Closed-Loop。通过上面的例子可以看出，开环系统与闭环系统的核心区别在于是否进行输出信息或状态信息的反馈，即例子中的个人位置信息反馈。相反的，闭环系统增加了反馈环节，虽然导致系统成本上升，并会降低响应速度，但能使整个系统更加“稳定”，因此绝大多数系统都是采用闭环结构，开换系统只针对少数情况。......
2023-07-05
-
电力系统动态频率特性分析详细阅读
电力系统的动态频率特性是指当电力系统由于某种原因，使系统有功功率平衡遭到破坏，系统频率将从额定频率值过渡到频率恢复值所经历的动态过程[11]。目前，当我们研究电力系统频率动态过程以及低频减载方案整定时，为了频率统一变化，分析相对简单，通常采用单机带集中负荷的模型来设计，用多机系统来校验。所以分析简单系统动态频率特性是至关重要的。......
2023-06-29
相关推荐